計算アルゴリズム

ランジュバン方程式とは、ポテンシャル中を運動するブラウン粒子に対する運動方程式（確率微分方程式）である。

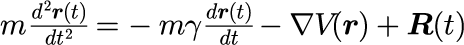
右辺の第１項目は速度に比例する粘性力、第２項目はポテンシャルによる力、第３項目はランダムな外力である。 本稿では重力場におけるシミュレーションを行う。重力場のポテンシャルは

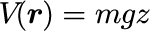
で与えられる。ランダムな外力は

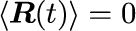
を満たすと仮定する。本稿で取り扱う計算アルゴリズムは、 この２階の微分方程式を１階の連立微分方程式とし、オイラー法を用いて方程式を差分化する。

１階の連立微分方程式

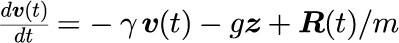
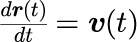
１階の連立差分方程式

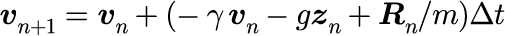
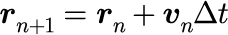
シミュレーションでは、計算パラメータ（時間間隔、重力、粘性係数、外力、質量）を動的に変更可能である。

メモ：揺動散逸定理

本シミュレーションとは直接関係はないが、ランジュバン方程式から導かれる重要な事項をまとめておく。 ランダムな外力が

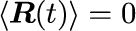
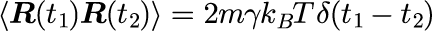
を満たすガウス過程の場合、ランジュバン方程式を満たす多数の粒子系に対する密度分布は 拡散方程式並びにフォッカープランク方程式を導出することができる。 これらの方程式から得られる密度分布の定常解は、カノニカル分布と一致するべきとの考察から、 拡散係数と粘性係数との関係であるアインシュタインの関係

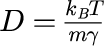
が導き出される。