ガウス分布のパラメータ
| 最小 | sigma: | 最大 |
| 0.001 | 1 | |
| 最小 | x0: | 最大 |
| -1 | 1 | |
| 最小 | y0: | 最大 |
| -1 | 1 |
計算アルゴリズム
ガウス分布とは次式で与えられる連続変数に対する確率分布の一つで、正規分布とも呼ばれる。
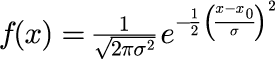
ガウス分布が重要な理由は、「任意の確率分布関数に従う独立変数の平均値の分布は、独立変数の数が大きくなるにつれガウス分布に近づく」 という中心極限定理の存在により、統計学上特別な性質を有するためである。 また、「ガウス分布のフーリエ変換によって得られる関数もガウス分布となる」という事実は、 ガウス分布がフーリエ変換を多用する数学や物理学の分野では非常に重要な役割を演ずることを意味する。
本稿では、次式で与えられる2次元ガウス分布を考える。
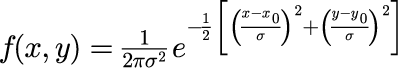
ただし、最大値を「1」としたいため、本シミュレータでは係数を「1」とする。