地震と津波の教育プログラム　―仙台市科学館にて―

１月１７日にNHKのニュースで放送された「地震と津波の教育プログラム」について報告します。 東北大学工学部災害制御研究センターの今村教授と仙台市科学館が共同開発した地震と津波の理科実験を見学しました。　仙台市科学館で仙台市の中学生を対象に地学の授業の一環として実施されているプログラムです。 自然の仕組みを探求することから防災意識を高める教育プログラムでした。津波の伝搬速度に興味をもったので、理論の構築と実験をしていこうと思っています。
【参考】仙台市科学館「科学館学習」

教育プログラムの目的の紹介

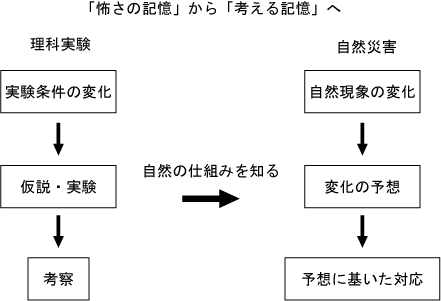
世界的みても、日本は天災が多い国である。特に宮城県は宮城県沖地震が周期的に起こっている。従来の防災教育においては、被害状況をみせ、怖さという記憶により災害時の対応がとれるとされてきた。しかし、そもそも恐怖という記憶では思考が深まらないおそれがあり、状況に応じて行動することはできない。
では災害時における対応のアイデアがわかすには、どのような教育が必要なのだろうか。「なぜ、災害がおこるのか？」という仕組みを理解することが必要である。自然現象が人間社会にとってインパクトになった時に災害となるが、災害は自然の現象のひとつである。自然の仕組みを知るという意味で、防災教育における理科実験の必要性がうまれる。理科実験において、仮説をたて実験条件をかえながら、検証のための実験を行い、考察するプロセスが、自然の災害において変化を予測し、適切な行動をとる思考力の育成につながる。つまり自然現象のしくみを理解することで、災害時における対応がとれる。防災教育の土台としての理科実験の教育プログラムを今回、紹介する。

津波の実験

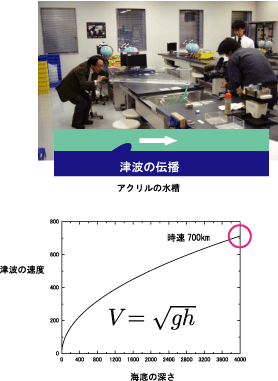津波の発生原因は、地震によって海底に断層が生じることによる海底の地表面の上下方向の変化である。その地形変化が水を伝搬し海面に現われ、水位の変動がうねりとなって周囲に拡大していき、津波となる。津波は波の伝搬という自然現象の一部であり、津波の伝搬速度は海底の深さが大きいほど速い。例えばチリ沖で地震が発生したとすると、十数時間で日本に到達する。海底が深いところでの津波の速度は時速７００ｋｍほどにもなる。
このアクリルの水槽でつくられた実験装置は、水槽の水の深さによって、波の伝搬速度がかわることを定量化する装置である。実際、水槽の左端で波を発生させ、右端に波が届くまでの時間をストップウォッチで測定し、波の到達時間をはかると、深さの平方根に比例した波の伝搬速度がえられる。津波が発生するしくみを理解し、波の伝搬速度を理解することで、津波という自然現象を体感する。

津波の速度

水面に石を投げると、波紋が広がっていく。　石が水を押しのけ、水の変形が水面を伝わっていく。この波紋の広がりは水が重力を受けていることを前提に、水の圧力の変化が伝わっているのである。石の水面への衝突によって、盛り上がった水は重力の影響をうけ、同じ深さにおける圧力が他の場所よりも高い。この圧力の高低によって波紋が伝搬していく。伝搬するのは、波の形（圧力やエネルギーといってもよい）であり、水という物質が動いて、波が伝搬しているわけではない。
波形が波紋の伝搬と津波の伝搬は本質的に同じ現象である。以下に波の伝搬の速度を求める。

波の伝搬と流体の伝搬

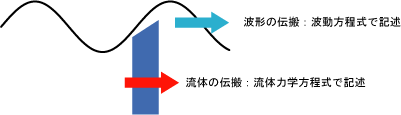
まず波形の伝搬と流体の伝搬は別の基礎方程式で扱う。表面における波形の伝搬は波動方程式で記述する。水面下における流体の伝搬は流体力学方程式で記述する。次に波形の伝搬と流体の伝搬の因果関係を考え、波形の伝搬の速度を求める。重力が存在する中で、表面の波形によって水面下の流体にかかる圧力がかわり、圧力差によって流体が運動し、波形が変化する。波形が変化することで、水面下で圧力差が起こり、、、が繰り返されている。
計算の方針は、左辺の時間に関する変化量は微分で記述し、右辺の空間に関する変化量はまず差分で記述し、次に微分形式にする。２次以降の非線形項は近似として落とす。

波動方程式

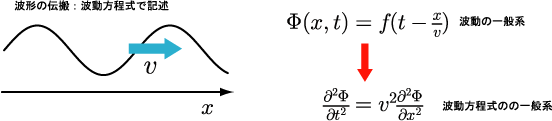
1次元の波の伝搬を考える。波の時間ｔ、場所ｘにおける波の位置を記述することを考える。原点においての振動がｔ－ｘ/v時間後に、場所ｘに伝わる。波の形が変わらないことを前提にすれば、この方程式から、波の位置が満たすべき、時間と空間の微分方程式が得られる。２階の微分方程式からなり、波形の伝搬速度ｖが係数として現れている。
この方程式は、波動方程式とよばれ、波形が伝搬する場合の一般的な方程式である。例えば、弦の振動の場合の伝搬速度は張力と弦の密度に依存する。水面における波の伝搬速度を求める場合、流体の運動方程式を解いて、波動方程式の形にもっていき、伝搬速度ｖを流体に関する特徴的なパラメータで記述すればよい。

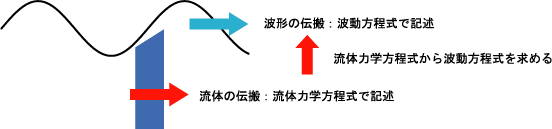
流体力学的方程式：運動方程式

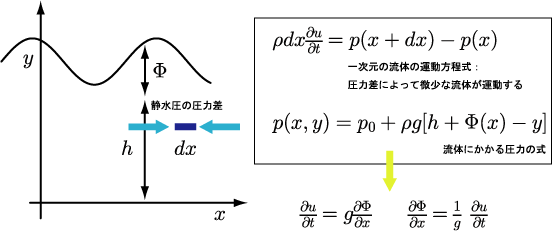
次は水面下に目を向ける。流体はｙ方向に関しては運動しないので、ｘ軸に関する一次元の流体の運動方程式をたてる。まず前提となるのは静水圧である。流体のある一点をとれば、一点には全方向から等しい圧力がかかる。つまり、ｙ軸方向からかかる圧力はx軸方向にかかる圧力に等しい。波の高さがことなる場合、y軸方向に圧力差がｘ軸方向の圧力差を生む。x軸方向の一次元の流体は、この圧力差をうけて運動する。ナビエストークス方程式から考えると、流体の速度uが十分小さいとして、移流項を落とした。
流体がうける圧力は、単位の次元を考えると重力による位置エネルギーを距離の３乗で割ったものである。この演算は質量を密度にかえる。海面にもちろん大気圧がかかる。
以上の式から計算すると波形のｘによる微分、すなわち波形の接線の傾きに比例する力をうけて、流体がx軸方向に運動するという式が得られる。密度は両辺にかかっているので落ちてしまい、重力加速度が係数となっている。あるいは、波形の傾きは、流体の速度の時間微分、すなわち流体の加速度によっている。

流体力学的方程式：質量保存の法則

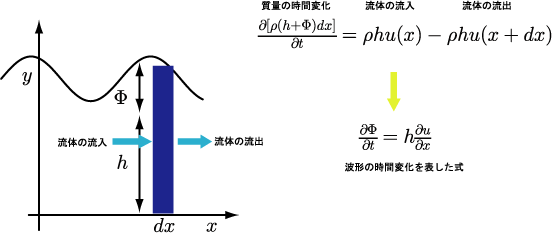
水面下に幅ｄｘで記述される微少体積を考える。この微少体積中の質量変化の式をたてる。流体の流入と流出によって、微少体積中の質量が時間的に変化すると考え式をたてる。最初、右辺は差分で記述するが、右辺において空間微分を実行すれば微分方程式がえられる。今度は波形の時間微分が流体の速度の空間微分によって表されている。係数は水の深さｈである。

流体力学的方程式：質量保存の法則

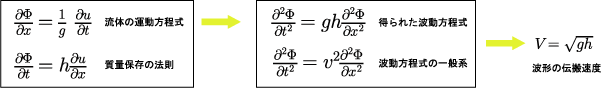
流体の運動方程式と質量保存の法則から、流体の速度であるuを消去することで、波動の伝搬の方程式を求める。得られた２つの式をそれぞれ位置ｘと時間ｔで微分すれば、波動方式が得られる。この式を波動方程式の一般的な式と比べることで、波形の伝搬速度を求める。得られた式は、波形の伝搬速度は重力加速度と水の深さによるというものである。単位の次元もあっている。密度によらないのは、重いものも軽いものも同時に落ちることと同様である。重力加速度は、運動方程式からきていて、水の深さは質量保存の方程式からきている。深いほうが波の速さが速いというのは不思議な気がするが、質量保存の要請からきている。

今度の予定

･液体のみの実験ならばある程度、理論的に解ける。しかし、実際の津波の場合、特に沿岸部においては砂の海底が存在する。砂も流体のように振るまうので、液体と砂が流体として運動したとき、どういった現象がおこるだろうか？砂がアクリルのケースの下に敷いたら、どのような波の伝搬速度が得られるだろうか？海底の砂にできる波紋もみてみたい。

･波形の伝搬をより小さなスケールで実験したい場合、どうしたらいいだろうか？　今回の式の導出ではっきりしたのは、波の伝搬速度は重力加速度と深さにしかよらないということである。月にいかない限り、実験条件はかえられないのか？

･砂でいろいろな形の海底をつくった時の波の伝搬速度を測定する。