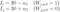活動と休憩の最適なバランスを求める

今回の疑問

実際にアリを見ると7割のアリが休んでいる。こんなに休んでいるのにすべてのワーカーは女王に出会うという。本当にもっと出会うのに効率がいい方法があるのではないか？

シミュレーションの方針～活動と休憩の切り替えについて～

アリのコロニーを見ると、7割のアリが休憩、3割のアリが活動をしていた。これをシミュレーションで再現したい。すべてのアリは活動・休憩のどちらのモードにもなると仮定すれば、再現する方法は2通りある。
①活動時間・休憩時間を等しくして、どちらのモードに入るかの確率を変化させる
②確率を等しくして、活動時間・休憩時間の比率を変化させる
①、②について図を使って説明する。

①活動時間・休憩時間を等しくして、どちらのモードに入るかの確率を変化させる

1匹のアリの活動・休憩について、↑の点まで時間が経ったら、休憩・活動のどちらのモードに入るかを決める。ただし、活動、休憩時間のどちらの時間も同じにする。このようなアリが複数いればある瞬間のコロニーをみれば、観察結果と同じ様子が見られるだろう。

例：1匹のアリの動きに注目すると

②確率を等しくして、活動時間・休憩時間の比率を変化させる

1匹のアリの活動・休憩について、休憩・活動のどちらのモードに入るかの確率を等しくする。ただし、↑の点まで時間を活動：休憩の比率を変更する。このようなアリが複数いればある瞬間のコロニーをみれば、観察結果と同じ様子が見られるだろう。

例：1匹のアリの行動について注目すると・・・

シミュレーションの方針～ワーカーの女王判別について～

オオツノハリアリを見た際、琉球大の見解である女王がワーカーを追いかけるという行動だけでなく、ワーカーが女王に近づいていくように見えた。これをシミュレーションに組み込み、休憩・活動の切り替えとあわせて最も女王とワーカーが出会うのに効率のいい動き方を探したい。ここでは、ワーカーが女王を見つけて女王の方へ近づくというアルゴリズムの方針を説明する。
シミュレーションではアリを1ピクセルの点と見立て4方向に進むようにする。通常は4方向を等確率で決定するがもしある程度の範囲内に女王がいた場合、その方向へ行く確率を大きくする。

シミュレーションの方針～アリ同士の接触の判別について～

先ほどのようなアリのアルゴリズムを考えた上で実験を行う。実験を行い、女王がすべてのワーカーに会うのにどれくらいの時間がかかったのかを測定したい。このときに考えなければいけないのはアリ同士の接触の判断である。接触方法は二通り考えられる。
①点が重なったかどうかで判断する
②点同士が隣接した段階で判断する。点同士が重ならないようにする（排除体積を考慮すると言うらしい）
①の考え方はプログラミングで再現する上では考えやすい。座標が重なったかどうかの判断はすぐ考えられる。しかし、重なりを許可してしまうと面倒なことが起きる。それは女王の周りにいくらでもワーカーが群がることができるという問題が生じる。したがって、女王は止まってワーカーが近づくようなモデルが最適な状態になると思われる。これに対して②の場合はいくら女王の周りに集まっても5匹以上は同時に接触できない。もし女王が動いて接触しているワーカーを振り払えばより多くのワーカーと接触できる。すなわち、女王が動く必然性がはっきりと出てくるのだ。
まずは考えやすい①でシミュレーションを行い、次に②の排除体積の考慮も入れて考えたい。

シミュレーションの予想

以上のような実験条件で最も女王とワーカーが出会うのに最適な動き方を考える。ここでどのような結果が得られるか予想をしてみる。今回の実験の制御する要素である「活動時間と休憩時間の比」を横軸、「活動モードに入る確率」を縦軸にした僧都を用いて考える。各パラメータごとに女王とワーカーが出会うのに何ステップ掛かったかを10数回調べその平均を僧都に記述していきたい。イメージとしては平均値によって色分けをして載せたいと思う。

アリの休憩・活動の相図の見方

①ワーカー、女王ともに完全にランダムで動いた場合
（「ワーカーが女王を見つけたら近づく」などのアルゴリズムを入れない）

予想としては活動・休憩が等確率の部分が最も効率がよいのではないかと考えた。すべてのアリが完全にランダムで移動するので極端にアリが休憩ばかりしない限りはほぼ同じような結果が出るのではないかと考えられる。

②ワーカーが女王を判断し近づくことができる場合（ただし排除体積は考慮しない）

ワーカーが女王を判断できるのであれば、よりワーカーが活動すれば活動するほど女王に近づくことができるはずである。さらに、女王のみは常に休憩をしていた方がより出会う効率はよいだろう。なぜならばワーカーが近づくならば目標（女王の座標）は固定された方が近づきやすいからである。

③ワーカーが女王を判断し近づくことができる場合（排除体積も考慮する）

女王とワーカーが重なることができない場合、②とはかなり結果は違ってくるのではないだろうか。なぜならば、女王にワーカーが群がれば群がるほど女王の周りはアリだらけですべてのワーカーが接触するのは逆に難しくなるからである。その場合むしろ女王もワーカーも活動をしない方が効率が良いのではないだろうか？すなわち、混雑しない程度に全体が活動することで効率があがるのでは？という予想である。