VisualC++ と OpenGL を利用した仮想物理実験室
【2-1-1】加速度・力・質量の関係：ニュートンの運動方程式

文責：遠藤理平（2010年1月10日）カテゴリ：コンピュータ・シミュレーション講座授業日誌(81)｜仮想物理実験室(325)

第１章では、時刻 t[s]、位置 r[m]、速度 v[m/s]、加速度 a[m/s^2]、加加速 j[m/s^2]と物理量の定義を行い、対応する運動（等速度直線運動、等加速度直線運動、等加加速度直線運動）についてのアルゴリズムの構築と、シミュレーションの実行を行ないました。しかしながら、これまで定義した物理量には、これらの運動が「どのようにして」起こるのかという情報は含まれていません。本章では、運動を引き起こす物理量「力」を定義することから始めます。

力と加速度

位置 x=0[m] に静止している物体があるとします。日常的な感覚では、このまま外から何もしなければ物体は動き出すことはないし、外から「力」が加えられればきっと動き出すことでしょう。これは物体に「力」という物理量が加えられた瞬間に、速度 v=0[m/s]から速度が大きくなる（加速する、加速度をもつ）ということです。また「力」は大きいほど、より大きな加速を得ることも直感的です。「力」という物理量を「加速度[m/s^2]」との関係を次のように仮定します（「力」の単位はまだ決まりません）。

「加速度」と「力」の関係式

(5-1)

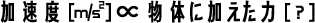
上記の関係式は、「加速度」と「力」は比例関係にあることを表しています（「∝」は「比例関係」を表す数学記号です）。逆の言い方をすれば、「加速度」に比例する量を「力」と定義するということです。

また一方で、物体の加速には「力」だけではなく、物体の「重さ」も関連があることも我々は日常生活で知っています。同じ「力」が加えられたとしても、軽い物体は加速しやすく、また逆に重い物体は加速しにくいでしょう。物理学ではこの因果関係を、「力」を加えたときの物体の加速しにくさとして物理量「質量[kg]」を定義します。

物理量５「質量」：（「加速のしずらさ」を表す物理量）

(5-2)

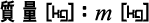
この「質量」と「加速度」は反比例の関係になります。逆の言い方をすれば、「加速度」に反比例する量を「質量」と定義するということです。

「加速度」と「質量」の関係式

(5-3)

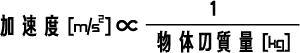
上記の２つ式(5-1)と式(5-3)を組み合わせることで、「加速度」と「質量」「力」の関係式が導かれます。

(5-4)

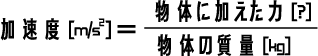
上記の関係式から「力」の単位も決定でき、新しい物理量「力」を定義します。

物理量６「力」（１次元）

(5-5)

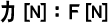
力の単位

(5-6)

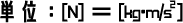
新しく定義した物理量「力[N]」を用いて、上記の式は次のように表すことができます。

(5-7)

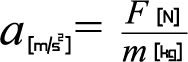
この式は、質量 m[kg]の物体に力 F[N]を加えたら（右辺）、物体は加速度 a[m/s^2]で運動する（左辺）という因果関係を意味します。つまり、質量 m[kg]と力 F[N]がわかっていれば、加速度 a[m/s^2]が決まるという意味です。この式を移項して、力 F[N]を左辺にする。

(5-8)

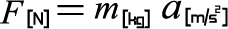
この式は数学的には単に恒等式を移項しただけですが、物理学因果関係が逆になり、意味が異なります。物体の質量 m[kg]を加速度 a[m/s^2]で運動させたら（右辺）、物体には力 F[N]が加えられている（右辺）という因果関係を意味します。つまり、質量 m[kg]と加速度 a[m/s^2]が判っていれば、力 F[N]が決まるという意味です。また、3次元空間では、速度 v[m/s]、加速度[m/s^2]同様にベクトル表すことができます。

物理量６「力」（３次元）

(5-9)

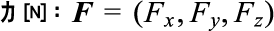
地球の重力加速度の測定

我々は日常生活で、地球上では重力が働いていることを知っています。このことは非常に古くからも知られていたということです。様々な質量 m[kg]を持つ物体を重力に従って運動させます。時刻 t=0[s] からの運動をはじめ、時刻 t[s]と位置 x[m]の関係を測定します（中学3年生で学習する力学台車の実験です）。計測結果から計算することで、速度 v[m/s^2]、加速度[m/s^2]、加加速度[m/s^3]が得られます（速度の求め方：【２日目】等速度直線運動、加速度の求め方：【３日目】等加速度直線運動、加加速度の求め方：【４日目】等加加速度直線運動を参照ください）。

その結果は、どんなの質量 m[kg]の物体でも、加速度 a = 9.80665[m/s^2]で等加速度直線運動を行ないました。この重力による特別な加速度は重力加速度 g[m/s^2]と呼ばれます。

物理定数１：重力加速度

(5-10)

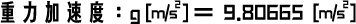
重力と重さ

物体が地球からの重力で加速運動する場合（a = g[m/s^2]）、物体に作用している力 F[N]は、式(5-8)で求めることができます。つまり、F[N] = m[kg] × g[m/s^2] となります。この力は物体に働く重力を表しています。我々が普段の生活で「重い」「軽い」と感じているというのは、この「物体に働く重力の大きさ」を指しているのです。新しい物理量「重さ[N]」を定義します。

物理量７：重さ（物体に働く重力の大きさ）

(5-11)

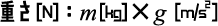
重さの単位は[N]の他に[kgw](キログラム重)があります。普段の生活の中では、質量[kg]と重さ[N]を混同しています。例えば、「2リットルのペットボトルの重さは 2[kg] です」という表現は、正確には間違いです。正しくは、「2リットルのペットボトルの質量は 2kg です」、もしくは「2リットルのペットボトルの重さは 2×9.80665[N] です」と表現しなければなりません。

ニュートンの運動方程式

次に、式(5-8)の恒等式の辺々を移項して、左辺に質量 m[kg] 加速度 a[m/s^2]、右辺に力F[N]を持って、次の関係式導きます。

ニュートンの運動方程式（１次元）

(5-12)

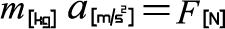
この関係式は、力 F[N]を加えたら（右辺）、質量 m[kg]の物体が加速度 a[m/s^2]で運動する（左辺）という意味を表しています。これは式(5-7)とほぼ同じ意味を持ちますが、物体のに関する情報がすべて左辺にあり、式(5-7)と比べて、力と物体の運動との因果関係が明示的になります。これはニュートンの運動方程式と呼ばれ、我々が生活しているスケールで成り立つ方程式として知られています。

またこの方程式は、3次元空間ではベクトルで表します。

ニュートンの運動方程式（３次元）

(5-13)

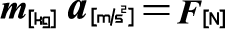
ベクトルで表した場合、加速度 a[m/s^2]と力 F[N] のそれぞれの x, y, z 成分で成り立ちます。

(5-14)

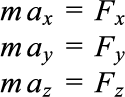
【５日目】「重力加速度、重力、ニュートンの運動方程式」では、シミュレーションはありませんでした。次の章からは、この方程式を利用して様々な運動をシミュレートしていきます。