シュレディンガー方程式に従う粒子の時間発展
無限に深い２次元井戸型ポテンシャル

前回の無限に深い井戸型ポテンシャル（１次元）に引き続き、２次元の場合の描画を行ないます。
下図のような、一辺が L=10[nm] の２次元井戸型ポテンシャルを想定します。

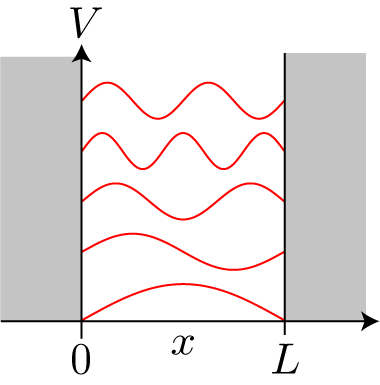
境界条件を考慮した結果の波動関数は次のようになります。

井戸型ポテンシャルの固有関数

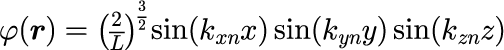
但し、k_{xn},k_{yn},k_{zn}は整数の組み (n_x, n_y, n_z) を用いて、

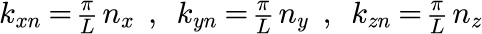
となります。波数kは飛び飛びの値を取ることになります。 固有関数が求まったので、時間発展を計算することができます。

ガウスパルスの時間発展

井戸型ポテンシャルの中に、電子がガウスパルス型分布をして閉じ込められている場合を考えます。 固有関数に時間依存部分を加え、ガウス分布型の重み付けをして、波数を足し合わせることで、ガウスパルスの時間発展を計算をすることができます。

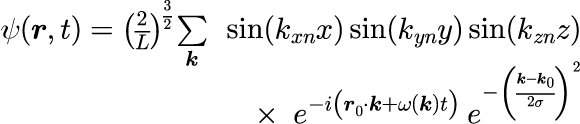
r_0 は実空間におけるガウスパルスの中心座標となります。

パルス幅を決めるσの基準σ_0の値

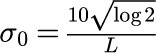
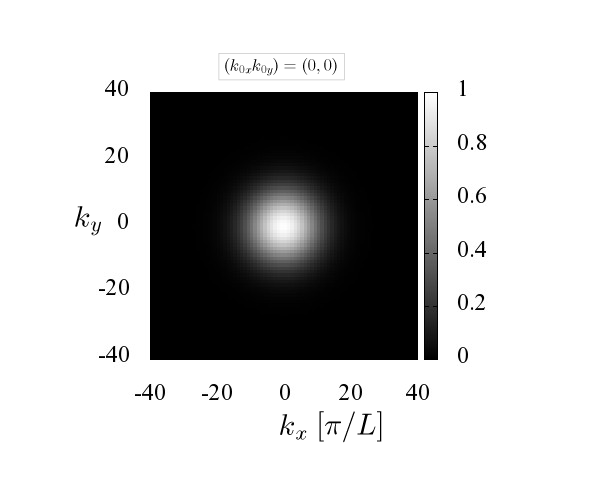
k_0=0, σ=σ_0 の場合の波数空間におけるガウス分布

k_0=0, σ=σ_0 の場合の時間発展

縦軸：実空間 x 0と10[nm]がポテンシャル障壁
横軸: 実空間 y 0と10[nm]がポテンシャル障壁
色：黒色→存在確率0
パルスの中心座標：r_0 = (L/2,L/2)
時間間隔： 10^{-15}[s]

シミュレーションの結果、約550[fs]の周期があることが分かります。

考察

考察については、また後日あらためて行ないます。

VisualC++ ＋ gnuplotによるアニメーション

後日あらためて公開します。