計算物理学　第１章序章
２－１．DLAによる樹木状クラスタのシミュレーション

本稿は、凝縮系物理を中心として広範囲にわたる計算手法に関して、そのアルゴリズムの導出から実装までを丁寧にまとめられていることで知られている計算物理学 J.M.ティッセン (著), (訳) 松田 和典, 道廣 嘉隆, 谷村 吉隆, 高須 昌子, 吉江 友照を元に、 本書で取り扱われているテーマについて、具体的にC++言語にてプログラミングし、計算結果を gnuplot や OpenGL を用いて図や動画にすることを目的とします。

本書では計算物理学において、確率的シミュレーションの例として、DLAシミュレーションを取り上げています。 DLAシミュレーションとは、diffusion-limited aggregation の頭文字をとって拡散律則凝集と和訳され、結晶成長の単純なモデルとして考えられています。

DLAシミュレーションのステップ

DLAによる樹木状クラスタのシミュレーションは次のステップで行われます。

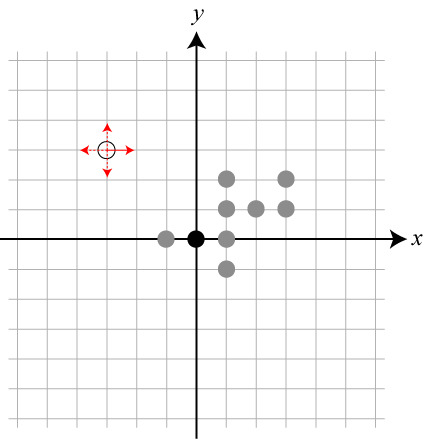
１．システムの中央に結晶の核がある
２．１個のブラウン粒子が遠方から近づいてくる
３．中央にある結晶の核に隣接すると、粒子は結晶化する
４．以後は同様に、ブラウン粒子が結晶化された粒子に隣接すると結晶化する

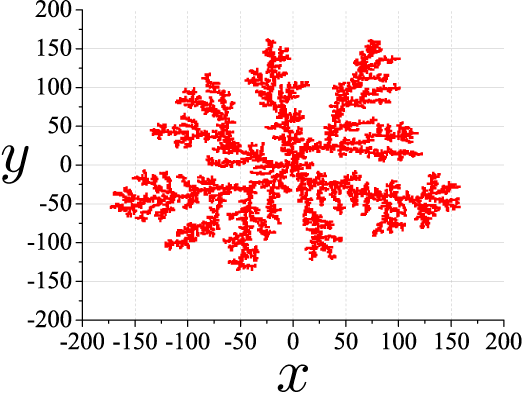
DLAシミュレーションの結果

パラメータとして、粒子数 N と吸着率 p を考えます。

粒子数 N = 10000
吸着率 p = 1

粒子数 N = 10000
吸着率 p = 0.1

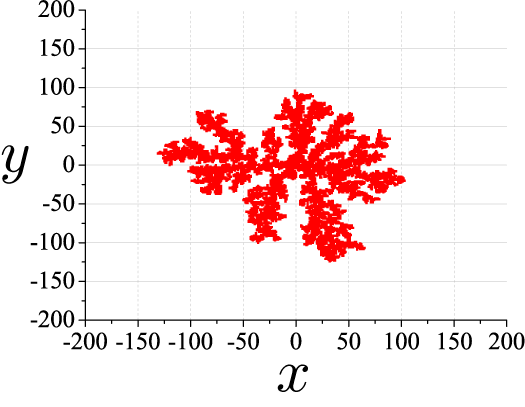
吸着率 p=1 の場合の比較して、全体的に縮こまっているように見えます。 これは、運動している粒子が外側で接触しても結晶化しないで、内側まで移動してくることが可能であるためだと考えられます。

C++プログラム

DLA シミュレーションを行うためには、擬似乱数が必要となります。 本シミュレーションでは、擬似乱数発生器として「メルセンヌ・ツイスタ」を利用します。

※擬似乱数発生器「メルセンヌ・ツイスタ」についてはこちらをご覧ください

本DLAシミュレーションは、中心から半径「R」（≫クラスタサイズ）の地点から、ランダム運動するとします。 半径「R」の値は、クラスタサイズとともに大きくしていきます。

 
//////////////////////////////////////////////////////////////////////////
// DLAシミュレーション
// DLA_メルセンヌツイスター.cpp
// ・吸着率を変更できる
//////////////////////////////////////////////////////////////////////////
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include <cstdio>
#include <iomanip>
#include <stdio.h>
#include <direct.h>
#include <mt19937ar.h> //メルセンヌ・ツイスタ
using namespace std;
double PI = acos(-1.0);
double e = 2.7182818284590452354;
//備考：画面サイズはデフォルトで、640×480
string folder = "data", ff="";  //保存フォルダ名

const int dimension = 2;//次元
const int N_max = 10000;//クラスタ構成粒子数
const int x_0 = 10000;//中心座標
const int y_0 = 10000;//中心座標
bool core[x_0*2+1][y_0*2+1] = {false}; //中心座標(0.0)＝配列中心[x_0][y_0]
int core_number = 0; // 固まった数

double R = 200.0; //粒子の出発する中心からの半径
double r = 1.0;   //クラスタの半径

//粒子クラス
class Perticle{
public:
  int D[dimension];
  Perticle(){
    for(int j=0; j<dimension; j++ ){
      D[j] = 0;
    }
		double theta=2.0*PI* mt::genrand_real1();  //mt::genrand_real1() は [0,1] でランダム
    D[0]= int(R*cos(theta));
    D[1]= int(R*sin(theta));
  }
  void Step(){
    int nn = int(dimension * mt::genrand_real1());
    double pp= mt::genrand_real1();
    if(pp>0.50) D[nn]++;
    else D[nn]--;
    if(core[x_0+D[0]][y_0+D[1]]==true){//排除体積効果
      if(pp>0.50) D[nn]--;
      else D[nn]++;
    }
    if(D[0] < -int(R)) D[0] += 2*int(R);
    if(D[0] >  int(R)) D[0] -= 2*int(R);
    if(D[1] < -int(R)) D[1] += 2*int(R);
    if(D[1] >  int(R)) D[1] -= 2*int(R);
  }
  void Restart(){
    double theta=2.0*PI*mt::genrand_real1();
    D[0]= int(R*cos(theta));
    D[1]= int(R*sin(theta));
  }
};

char str[200];
string str1;

int main(){
	#if defined(_MSC_VER)
		_mkdir(folder.c_str());   // Windowsフォルダ作成
	#endif
  mt::init_genrand((unsigned)time(NULL));

  for(int n=1; n<=9;n++){
    core_number = 0;
    r=1.0;
    R=200;
    // コアの初期化
    for(int i =0; i<=2*x_0; i++){
      for(int j=0; j<=2*y_0; j++){
        core[i][j] = false; 
      }
    }
    double probability = 0.1* double(n);//接触時の吸着確率

    ofstream fout_position;
		sprintf_s(str, "/DLA-%d.data", n); str1 = folder + str; 
		fout_position.open(str1.c_str());
    Perticle p[1];

    core[x_0][y_0]= true;
    cout << core_number <<" "<< 0 << " " << 0 <<" r=" << r << endl;
    fout_position  << 0 << " " << 0  << endl;

    while(core_number<=N_max){
      for(int i=0; i<1; i++){
        p[i].Step();
        if(core[x_0+p[i].D[0]+1][y_0+p[i].D[1]] == true || core[x_0+p[i].D[0]-1][y_0+p[i].D[1]] == true || core[x_0+p[i].D[0]][y_0+p[i].D[1]+1] == true || core[x_0+p[i].D[0]][y_0+p[i].D[1]-1] == true ){
          if(probability>=mt::genrand_real1()){
            core_number++;
            core[x_0+p[i].D[0]][y_0+p[i].D[1]] = true;
            if(pow(double(p[i].D[0]),2)+pow(double(p[i].D[1]),2) > pow(r,2)){
              r = sqrt(pow(double(p[i].D[0]),2)+pow(double(p[i].D[1]),2));
              R = (r+200.0)*2.0;
            }
            fout_position << p[i].D[0] << " " <<  p[i].D[1] << endl;
            cout << "n=" << n << " " << core_number << " " << p[i].D[0] << " " << p[i].D[1] << " r=" << r << endl;
            p[i].Restart();
          }
        }

      }
    }
    fout_position.close();
  }
}

課題メモ

１．DLAによる樹木状クラスタのフラクタル次元の計算を行う。
２．gnuplot を用いてクラスタの成長のアニメーションを作成する。

ミスの指摘、質問、コメントなどがございましたら、HTMLフォーム、もしくはinfo:natural-science.or.jpから、お待ちしております。

目次

第１章　序章

• １－１．Duffing振子のカオス的運動のシミュレーション
• １－２．Duffing振子の位相空間上でのカオス的運動のアニメーション
• １－３．Duffing振子の位相空間上のストレンジ・アトラクタに対するフラクタル次元
• ２－１．DLAによる樹木状クラスタのシミュレーション
• ２－２．DLAによる樹木状クラスタのフラクタル次元

第２章　対称ポテンシャルによる量子散乱

ゴール：水素原子のクリプトン原子による散乱に対する散乱断面積の計算

• ・ヌメロフ法による常微分方程式の解法
• ・球ベッセル関数
• ・ルジャンドル多項式
• ・位相シフト→断面積を計算するアルゴリズム

その他

• ・擬似乱数生成器：メルセンヌ・ツイスタの使い方
• ・ランダムウォークによる擬似乱数の比較：C言語rand関数とメルセンヌ・ツイスタ(mt19937ar)