マクスウェル方程式とシュレディンガー方程式　導入
【0-1】はじめに

本稿の目的

電磁気学のマクスウェル方程式と量子力学のシュレディンガー方程式は、物理学の基礎方程式の一つです。 マクスウェル方程式で出現する電場や磁場はベクトル関数であるのに対し、シュレディンガー方程式における量子粒子の波動関数はスカラー関数となり、 ２つの方程式は全く異なるように見えます。 しかしながら、特定の物理系では２つの方程式は同様の数学的取り扱いが可能となります。 具体的には、屈折率の異なる媒質が周期的に並んだ構造中（フォトニック結晶）の光の系と、 井戸型ポテンシャルが周期的に並んだ構造中（クローニッヒ・ペニーモデル）の電子の系では、転送行列法を用いることで同等に扱うことができます。 しかしながら、数学的に同等の形式であるにも関わらず、主役となる光と電子の性質の違いにより、異なる挙動を示します。 さらに、光パルスや電子パルスの伝搬といった動的性質の違いはさらに明白となります。

本稿の目的は、マクスウェル方程式とシュレディンガー方程式がもつ性質の一端を２つの系を比較することで浮き彫りにすることです。 一般の教科書では、１次元フォトニック結晶やクローニッヒ・ペニーモデルに対する転送行列から、複素透過係数や複素反射係数を定義し、単一エネルギーの静的性質については議論されています。しかしながら、パルスの伝搬といった動的性質はあまり一般的に知られていません。 本稿で扱うパルス伝搬などの動的問題に関するシミュレーションや解析解に対して参考になれば幸いです。 また裏の目的は、筆者が博士課程在学中勉強のために行ったシミュレーションに関する備忘録（個人的には真の目的）です。 本稿で取り上げたシミュレーションのC言語によるプログラムソースやgnuplotによるアニメーションを作成するテンプレートなども公開します。 マクスウェル方程式やシュレディンガー方程式の学習だけでなく、数値計算の学習の一助となればさらに幸いです。 なお本稿は、電磁気学と量子力学の基礎を学習した物理学部２年生から３年生を対象としています。

筆者の博士論文の紹介

筆者は2011年9月に博士号（理学）を取得しました。 博士論文の内容は、フォトニック結晶と呼ばれる屈折率の異なる媒質が周期的に並んでいる構造中の光パルスの伝搬についての理論的な研究です。 光パルスを長さ L のフォトニック結晶に入射してから透過するまでの時間を横断時間 τ と定義したときに（下記の図を参照）、 τ と L の関係を解析的に導出したのが本研究の内容です。

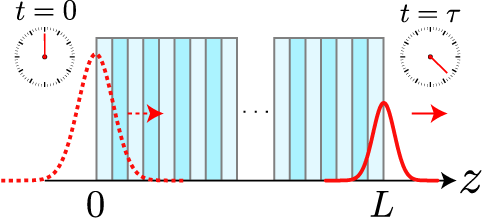
２種類の媒質でつくられるフォトニック結晶の模式図と、結晶サイズ L、横断時間 τ の定義

光は結晶内の境界面で反射を繰り返しながら進むため、単純な問題のわりにパルス伝搬の取り扱いは簡単ではありません。 本論文の一番のポイントは、周期構造に限らず、自己相似構造と呼ばれる非周期構造でも同様の取り扱いで、τ と L の関係を解析的に導出できることを示した点です。 本稿では博士論文の内容に詳細には触れませんが、もし興味のある方がおりましたら、PDFファイルを送りますのでご連絡いただければと存じます。

媒質中（絶縁体）中の光

光（電磁波）とは、空間中で電場と磁場が互いに電磁誘導によって交互に発生し合うことで生まれる波（波動）です。 ガラスなどの絶縁体中では、光は原子によって束縛されている電子と相互作用しながら進むため伝搬速度が遅くなります。 真空中の光の速度 c[m/s]と媒質中における光の速度 v[m/s] は

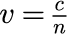
の関係があることが経験的に知られています。 n は屈折率と呼ばれる無次元の定数で物質によって異なり、n が大きいほど物質中の光の伝搬速度は遅くなります。 屈折率はおよそ、真空 n=1、光学ガラス n=1.5、酸化チタン n=2.5、程度で、大きなものでも３程度です。 屈折率は速度の比を表すだけでなく、名前の通り光の屈折現象におけるスネルの法則（入射角、反射角、屈折角と屈折率の関係）と関係があります。 スネルの法則については「反射波と透過波」の節で詳説します。

屈折率 n の大きさを得るには、本来、量子力学による精密な議論を必要としますが、 フォトニック結晶のように媒質の構造によって 光を反射させたり透過させたり曲げたりすることだけを考える場合には、 媒質の違いを屈折率の違いだけを考慮するだけで十分です。 屈折率のように、考えたい空間やエネルギーのスケールに対して、それよりも小さいスケールにおける現象の詳細を考慮せず、 引き起こされる巨視的なスケールの現象に対する結果だけで決められる物質固有の定数は、物質定数と呼ばれます。 本稿では、物質の違いを屈折率だけで議論し、屈折率の空間分布と光伝搬との関係を議論します。

フォトニック結晶について

本稿では、異なる屈折率をもつ媒質を周期的に並べたフォトニック結晶と呼ばれる人工構造物における光の伝搬を考えます。 周期はおよそ光の波長程度です。フォトニック結晶は空間周期性により１次元、２次元、３次元と分類されます。

フォトニック結晶の模式図

フォトニック結晶を構成する媒質は、真電荷や電流がない絶縁体（誘電体）とします。 フォトニック結晶中の光はマクスウェル方程式で記述することができます。 本稿では、１次元フォトニック結晶中の光パルスの伝搬について、シミュレーションと解析解について議論します。

【目次】シュレディンガー方程式とマクスウェル方程式

• ０．導入
  　【0-1】はじめに
  　【0-2】本稿で取り扱う基礎方程式
• １．一様媒質中における一般解と具体例
  　【1-1】一般解の表式
  　【1-2】平面波の時間発展
  　【1-3】１軸ガウシアンによる光パルスと電子パルス　（１軸ガウシアンによる電子パルスの拡散）
  　【1-4】２軸ガウシアンによる光パルスと電子パルス　（２軸ガウシアンによる電子パルスの拡散, ２軸ガウシアンによる光パルスの拡散）
  　【1-5】３軸ガウシアンによる光パルスと電子パルス
  　【1-6】垂直１軸ガウシアンによる光ビームと電子ビーム
  　【1-7】垂直２軸ガウシアンによる光ビームと電子ビーム
  　【1-8】直線偏光と円偏光
  
• ２．異なる媒質の境界における電磁波と電子波
  　【2-1】異なる媒質の境界における波動の一般論
  　【2-2】電磁波に対する透過係数と反射係数の導出
  　【2-3】電子波に対する透過係数と反射係数の導出
  　【2-4】境界面において任意の形状の波に対して時間発展を与える一般表式
  　【2-5】境界面における平面波電磁波の時間発展
  　【2-6】境界面における平面波電子波の時間発展
  　【2-7】境界面における１軸ガウシアンによる光パルスと電子パルスの時間発展
  　【2-8】境界面における２軸ガウシアンによる光パルスと電子パルスの時間発展
  　【2-9】境界面における３軸ガウシアンによる光パルスと電子パルスの時間発展
  　【2-10】境界面における垂直１軸ガウシアンによる光ビームと電子ビームの時間発展
  　【2-11】境界面における垂直２軸ガウシアンによる光ビームと電子ビームの時間発展
  
• ３．転送行列法
  　・電子のトンネル確率
  　・光のトンネル効果
  
• ４．１層バリアにおける光パルスと電子パルスのシミュレーション
• ５・ポテンシャル障壁による量子粒子のトンネル時間
• ６・フォトニックバンドギャップによる光パルスのトンネル時間
• ７．無限周期構造中の分散関係，群速度，位相速度
  　・転送行列とブロッホの定理
  　・ブロッホ波数と透過係数の関係
  　・分散関係
  　・透過係数と群速度の関係
  
• ８．有限サイズの結晶における光パルスと電子パルスの横断時間
  　・光パルスと電子パルスの横断時間の導出
  　・パルス伝搬速度と群速度の関係
  
• ９．フォトニックバンド端における光パルスの遅延
  　・１次元フォトニック結晶における透過係数と横断時間の数値計算
  　・横断時間の解析解
  
• １０．バンド端における電子パルスの遅延
  　・１次元クローニッヒ・ペニーモデルにおける透過係数と横断時間の数値計算
  　・横断時間の解析解
  
• １１．非周期構造における光パルスと電子パルスと伝搬