2次元量子力学における調和振動子
任意の初期空間分布+任意の中心運動量に対する時間発展
本稿では、1次元量子力学における調和振動子を次のステップで進めていきます。
・1次元量子力学の調和振動子における単一エネルギーの時間発展
・1次元量子力学の調和振動子における任意の初期状態に対する時間発展
・1次元量子力学の調和振動子におけるコヒーレント状態の空間分布
・1次元量子力学の調和振動子におけるコヒーレント状態の時間発展
・1次元量子力学の調和振動子における n励起状態の運動量表示
・1次元量子力学の調和振動子における任意の初期運動量分布に対する時間発展
・1次元量子力学の調和振動子における任意の初期運動量分布+任意の中心座標に対する時間発展
・1次元量子力学の調和振動子における任意の初期空間分布+任意の中心運動量に対する時間発展
・2次元量子力学の調和振動子の時間発展
前節「1次元量子力学の調和振動子における任意の初期運動量分布+任意の中心座標に対する時間発展」にて、本稿の目的である任意の初期状態に対する時間発展の計算手法を示すことができたわけですが、ここまでまとめている間にもっと簡単な方法に気が付きました。これまでの復習ついでに説明します。
任意の初期空間分布かつ中心運動量に対する時間発展を与える表式の導出
1.状態ベクトルを展開する
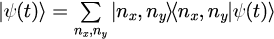
2.各因子にこれまでに得られている関数で表す
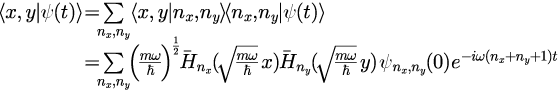
3.展開係数を与える表式
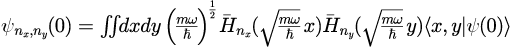
4.初期空間分布に虚数部を与えることで、中心運動量を
にずらす
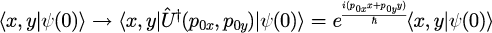
5.式(6)の初期空間分布をガウス分布とする
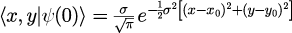
式(6)に式(7)を代入し、展開係数を得た後、式(3)に得た
を代入して和をとることで時間発展を計算することができるという手順です。
式(5)の中心運動量を移動させる表式は、運動量平行移動演算子を用います。
ガウス型運動量分布の時間発展
様々な初期値に対して、
、
アニメーションの時間間隔は、
です。
動画の正方形が
方向で、一辺が
です。
特に断りがない限り波動関数の絶対値を描画しています。
初期状態
初期状態
初期状態 の実部
の実部
一次元の時と同様、初期状態に依らず周期 で運動するようです。

































