数値計算法概論
常微分方程式の解法
本稿は、コンピュータを用いた常微分方程式の数値計算に関するアルゴリズムの個人的メモです。
数値計算に関する参考文献は図書やWEBなどで比較的簡単に入手可能で、それぞれ目的に合わせてまとめられていますが、
そもそもどんな手法が存在するのかを俯瞰するために網羅的に並べて、詳しく知りたい時のために引用文献を明記しました。
勉強する上で特に有用だったのが、専門家の方々がwww上で公開しているPDFファイルです。この場にて勝手に御礼申し上げます。
※本稿の内容は、私の誤解やミスを含んでいる可能性が非常に高いです。もしよろしければ、ご連絡下さい。修正、コメントなどを追記いたします。
常微分方程式の標準的な形式は
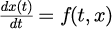
と表される。式(1)は1階の常微分方程式であるが、多階の常微分方程式の場合であっても階数に応じた変数を導入することで、1階の微分方程式の連立方程式に帰着される。つまり、式(1)を計算するための数値計算の手法(アルゴリズム)を確立することができれば、多階の常微分方程式も計算可能となるだけではなく、多変数による常微分方程式、偏微分方程式への応用も可能となる。
常微分方程式に限らずコンピュータで計算を行う場合、有限桁の精度で数値的に計算を行うことに起因する様々な問題が存在する[17]。 その詳細は割愛するが、計算アルゴリズムは問題を克服しながら、これまで多くの方々によって開発されてきた。 計算アルゴリズムに必要な要件は「精度よく」「安全に」そして「簡単に」という点にあり、それぞれに利点と欠点が指摘されている。 本稿では、次に挙げる分類をもとに、常微分方程式を計算するアルゴリズムを概観することにします。
分類
常微分方程式を数値的に解くための計算アルゴリズムの一般的な分類を概観する。
その前に表記についてです。と
における
の値を
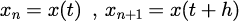
と表す。は
の差分量とする。
段階数(step)
を計算するアルゴリズムを
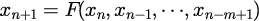
と表した場合、を段階数(step)と呼ぶ。
(1段階式)の場合、
を決めるために必要な過去のデータは
だけとなるため、
を初期条件から与えることで任意の時刻の値を計算することができる(セルスタート可能と呼ぶ)(ルンゲクッタ型など)。
一方、(多段階式)では、
を決めるために
だけでなく、より過去の情報
が必要となるため、このアルゴリズム単独だけでは計算をスタートできない(セルスタート不可能)(アダムス型など)。
多段階式の計算アルゴリズムは、各ステップにおける関数の値を利用して補間(ラグランジュ・ニュートン補間)を行う。
段数(stage)
を決定する際に
を評価する回数。計算量の目安となる。
段数1:アダムス型の多段階式に多い。
多段数:ルンゲ・クッタ型の1段階式に多い。
次数(order)
コンピュータを用いた数値計算は、微分を差分で表現することから生じる誤差を含むことになる。
とおき、計算アルゴリズム(差分式)による表式と
厳密解のテーラー展開から得られる表式
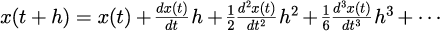
と比較して、低次から完全に一致する項数を次数(order)と呼ぶ。 次数が大きいほど厳密解と近いことを意味するため計算精度を表す指数となる。
陽的/陰的(explicit/implicit)
を計算するアルゴリズムが
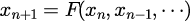
と表される場合、陽的アルゴリズムと呼ばれ、
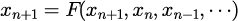
と表される場合は陰的アルゴリズムと呼ばれる。
陽的アルゴリズムは、を得るために必要な情報が、これまでに計算した
だけである。順々に代入するだけで時間発展を計算することができる(直接代入法)。
一方、陰的アルゴリズムでは、
を計算するために、
が必要となり、単純に代入するだけでは
を計算することができない。別途、ニュートン法などを用いて非線形方程式を解く必要がある。
陽的→プログラミングしやすい
陰的→硬い方程式でも安定的
シンプレクティック性?
位相空間の幾何学的な構造を不変に保つ変換をシンプレクティック変換と呼ばれる。
ハミルトニアン力学系に適用した場合、エネルギーや角運動量などの物理量が保存することに対応し、正準変換はすべてシンプレクティック変換であることが知られている。
シンプレクティック変換に基づいたアルゴリズムを用いて保存系における物理量の計算を場合、保存されるべき保存量が、一定の範囲内で保存されることが保証される。
一方、シンプレクティック変換に基づかない計算アルゴリズムの場合には、保存されるべき保存量が単調増加する。
シンプレクティック変換に基づいた計算アルゴリズムをシンプレクティック性を満たすと呼ばれる。
つまり、保存系の物理量を計算する場合には特にシンプレクティック性を満たすアルゴリズムが非常に重要な役割を果たすことになる。
シンプレクティック性○ → ベルレの方法、陰的ルンゲ・クッタ法 など
シンプレクティック性× → 陽的ルンゲ・クッタ法、予測子・修正子法など
欠点 → ステップごとに時間刻みを変えると保存量の保存が崩れる[12]。
対称型?
m段階式の計算アルゴリズム
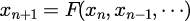
において、
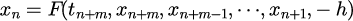
が成り立つ場合対称型アルゴリズムであると呼ばれる。
つまり、対称型アルゴリズムでは時間反転対称性が満たされている(ただし丸め誤差により厳密には成り立たない)。
対称型の利点はシンプレクティック性と同様、保存量が一定の範囲内で保存される[12]。
また、シンプレクティック性とは異なり、ステップごとに時間刻みを変えても保存量の保存が崩れないようにすることもできる[12]。また、任意の物理量の誤差が最悪でも時間に比例しかしないことも示されている[12]。
そのため、シンプレクティック変換に基づいたアルゴリズムよりもある意味でよい[12]。
対称型○ → 安定性が非対称型に比べ飛躍的によい[12]。
エルミート型
ラグランジュ・ニュートン補間で多段階式の計算アルゴリズムに対して、高階の導関数を利用して補間(エルミート補間)することで導出されるアルゴリズム[13]。 導関数が簡単に導出することが出来る場合、多段階式解法やルンゲ・クッタ法に比べて、誤差項の係数がずっと小さいことが知られている[13]。
安定性
コンピュータを用いた数値計算は精度が有限桁であるために、解析的には収束解存在していたとしても、数値的不安定性のために発散する可能性がある。 数値的不安定性は、線形安定性解析を利用することで定量化することができる。 線形安定性解析とは、写像力学における固定点の安定性を調べる手法の一つで、ある固定点近傍における振る舞いを支配するヤコビ行列の固有値と固有ベクトルを調べることである。振る舞いに主要な寄与を示すのは最大固有値の固有ベクトルで、最大固有値と固有ベクトルは写像に伴う拡大率と拡大軸のベクトルを表している。 厳密解近傍において、計算アルゴリズムによって計算した軌道の振る舞いを調べることによって数値的不安定性を解析することができる。 具体的には、任意の非線形方程式を原点周りで線形化した方程式である、テスト方程式と呼ばれる方程式
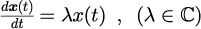
を用いて原点近傍の振る舞いを解析解と比較する。解析解は
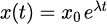
となるので、
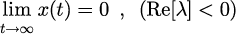
となる。一方、計算アルゴリズムをテスト方程式に適用して、と
の比を導出すると
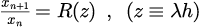
と表すことができる。ただし、は
の多項式となる。
この比は各ステップごとの拡大率を表すことになる。
つまり、
の条件のもと、
を満たす
の領域が安定性領域と呼ばれ、安定的に計算するための時間刻み
の大きさを決める指針となる。
当然、計算アルゴリズムによって安定性領域は異なり、安定性領域が広いほど
を大きくとることが可能となり計算効率を格段に上げることが可能となる。つまり、アルゴリズムの良し悪しを判定する一つの指標を与えることになる。
A-安定
安定性領域がを満たす計算アルゴリズムはA-安定と呼ばれる。
A-安定のアルゴリズムの場合、硬い方程式に対しても安定的であることが示されている[13]。
陰的ルンゲクッタ法の一部であるガウス・ルジャンドル法はすべての次数でA-安定であることが示されている[13]。
ルンゲ・クッタの公式
常微分方程式を解く計算手法のもっとも一般的な手法。
の値だけで高次近似を実現。
陽的、陰的どちらもあるが、一般的には陽的なものを指し、陽的4段4次の「古典的ルンゲ・クッタ公式」が最も有名。
系統的な導出により次数は無限に上げることができる。
陽的ルンゲ・クッタ法
陽的ルンゲ・クッタ法とはを決定するのに、
と
の近傍の複数地点における
を計算することで、高次を精度を実現する1段階多段式アルゴリズム。
具体的には
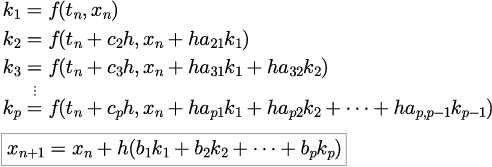
と表すことができ、
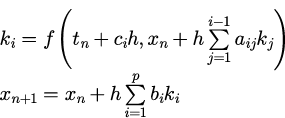
と形式的に表すことができる。
式(14)の係数は求める精度と段数から決まる。
与えられれば、
を用いて、
から
まで順に代入するだけで計算することができ、最終的に
が得られる。
係数
はアルゴリズムごとに異なり次のような表にまとめられる。

利点
・アルゴリズムの実装が簡単
・時間刻みの変更が容易。
・セルスタート可能[15]
・係数が有理数であるので丸め誤差が少ない(6段5位まで)[12]
・4次の安定性領域が低次よりも広い
欠点
・対称性×
・シンプレクティック性×[10]
→たとえ安定領域であっても保存すべき量が単調増加する
・陽的ルンゲ・クッタはA-安定ではない[13][20]
| 名称 | テーブル | アルゴリズム |
|---|---|---|
|
オイラー法 1段1次 |
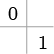
|
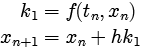
|
|
改良オイラー法 2段2次 |
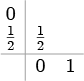
|
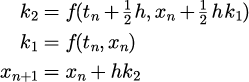
|
|
修正オイラー法(ホイン法) 2段2次 |
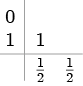
|
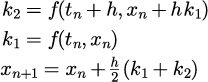
|
| ホインの3次公式 3段3次 |
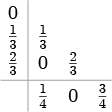
|
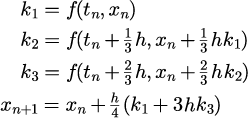
|
| クッタの3次公式 3段3次 |
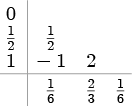
|
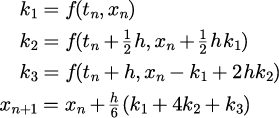
|
| 古典的ルンゲ・クッタ公式 4段4次 |
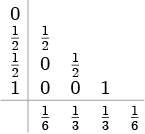
|
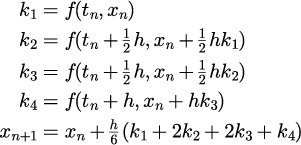
|
| クッタ3/8公式 4段4次 |
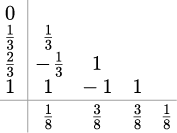
|
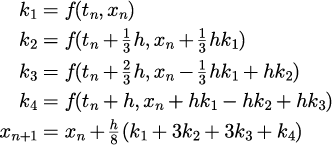
|
| ルンゲ・クッタ・ギル公式 | メモリが少なくて済む[3] | |
・時間刻みを埋め込み型で調整 → ルンゲ・クッタ・フェルベルグ公式[12]。
・系統的導出と安定性が掲載[3]。4次の丁寧な導出[6]。
・精度5次以上の掲載[7](Mathematicaを利用)。
・精度5次以上で安定領域がかなり狭くなる。
・古典的ルンゲ・クッタ公式は4段の公式であるため、分子動力学のように力の計算が体部分を占める系では非常に非効率となるだけではなく、
シンプレクティック性を満たさないため応用には適さない[10]。利用する場合は、少なくても刻み幅の適合化を行うべき[10]
・5段5次、6段6次と同等の公式も提案されている[8]
陰的ルンゲ・クッタ
陰的ルンゲ・クッタ法とは、陽的ルンゲ・クッタ法と同様にを決定するのに、
と
の近傍の複数地点における
を計算することで、高次を精度を実現する1段階多段式アルゴリズムである。
から
まで順に代入するだけで計算することができた陽的ルンゲ・クッタ法と異なり、
を決めるのに
を利用するというアルゴリズムになっている。
具体的には
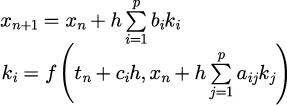
と形式的に表すことができる。そして一般的にはは式(16)で与えられる非線形方程式を解くことで得られる。
式(16)の係数
も、陽的の場合と同様に下の表のようにまとめられる。

「次数≦段数」である陽的な場合と異なり、陰的公式は「次数≧段数」を実現することができる。2段3次の既知の公式も多数知られている[21]。
本稿では、陰的ルンゲ・クッタ法の中でも
式(16)の係数が
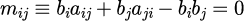
の条件を満たす特別な場合に絞る。式(18)は、少ない分点数で高精度の数値積分を行うガウス・ルジャンドル法と同様の概念を利用することで導出した条件で、式(18)を満たす陰的ルンゲ・クッタ法はガウス・ルジャンドル法と呼ばれる。 式(18)は、陰的ルンゲ・クッタ法のうちシンプレクティック性と満たす計算アルゴリズムであることが示されている[20]。
ガウス・ルジャンドル法の利点と欠点
【利点】
・すべて1段階 → セルスタート可能
・p段で2p次の精度を達成[12][20] → 計算量を減らせる
・シンプレクティック性○[13][20]
・対称性○[13][20]
・安定性 → A-安定[13][20]
・局所誤差 → 極小[13]
【欠点】
・を計算する際に非線形方程式を解く必要がある[13][20]
。
・埋め込み型公式が使えない。
| 名称 | テーブル |
|---|---|
|
ガウス・ルジャンドル法 1段2次 |
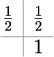
|
|
ガウス・ルジャンドル法 2段4次 |
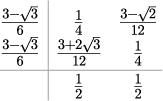
|
|
ガウス・ルジャンドル法 3段6次 |
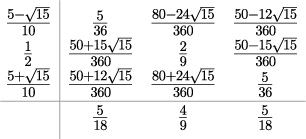
|
「A-安定+高精度+シンプレクティック性」を兼ね備えるため、多くの場合で最良[13]。
線形多段階法
を得るために、
しか利用しないルンゲ・クッタ法と異なり、
とより過去の情報を利用して解く方法は多段階法と呼ばれる。
共通の利点と欠点
利点
・何次の精度でも比較的簡単に導くことができる
・1ステップあたりの関数評価が1回で済む(1段)→ 計算量が少なくてすむ
・局所誤差が比較的小さい。
欠点
・シンプレクティック性×
・対称性×
・安定性 → A安定でない
・次数を上げると安定領域が急激に狭くなる → 予測子・修正子法である程度緩和可能[3]。
・セルスタート不可能 → 次数のあったルンゲ・クッタ法などを利用する必要がある
・多段階式からくる真の解には現れない計算モードを必ず含む[3]。
中点則(2段階2次)
多段階法の最も単純な陽的公式。
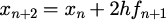
アダムズ・バッシュフォース公式
・陽的公式
詳細が[3]に記述されている。
ラグランジュ補間で多項式で近似し積分を計算する。2次から4次の公式を上から記述する。
5次6次の公式は[9]に記述されている。
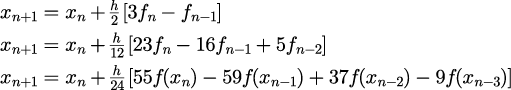
アダムズ・ムルトン公式
・2次が台形公式[12]。
・陰的公式
・計算スタート時に情報が足らない。
2次から4次の公式を上から記述する。
5次6次の公式は[9]に記述されている。
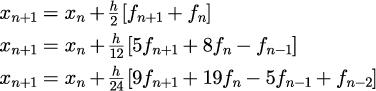
予測子・修正子法
予測子:アダムズ・バッシュフォース公式(陽的)
修正子:アダムズ・ムルトン公式(陰的)
を利用したものをアダムズ法と呼ばれる[3]。
[15]に係数の表。
4次のアダムズ法は次の通り。
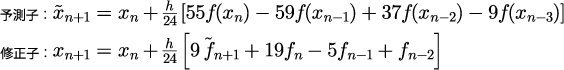
利点
・時間刻み間隔を簡単に変えられる[12]。
・誤差の評価が簡単[12]。
・自動的な精度制御も可能[15]。
・ルンゲ・クッタ法よりも高速[12]。
・収束するまで計算する必要はない。→1回で十分な精度[12]。
欠点
・安定領域が大きくない[15]。
・メモリが多く必要[15]。
・初期値の設定に難点 → 分子動力学シミュレーションの場合問題にならない[15]。
・ポテンシャルの不連続性に弱い[15]。
・力の不連続性に弱い[15]。
・力学と適合しない
・ハミルトン系に適用する場合は、最適化の余地がある[12]
シンプレクティック解法
先述の「分類:シンプレクティック性」でも触れたが、シンプレクティック解法とは、シンプレクティック変換に基づいたアルゴリズムである。
保存系における物理量の計算を場合、保存されるべき保存量が、一定の範囲内で保存されることが保証される。
これは保存系の物理シミュレーションで、長時間の計算を行う際に非常に有用となる。
ハミルトニアンの位置と運動量
の依存性が分離できる場合、陽的シンプレクティック解法を導出することができる。一方、ハミルトニアンの位置
と運動量
の依存性が分離できない一般のハミルトニアンに対しては、先述した「ガウス・ルジャンドル法」が陰的シンプレクティック解法となる。
本節では、陽的シンプレクティック解法に話を絞る。
ハミルトニアンが
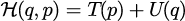
と分離される場合、正準方程式は
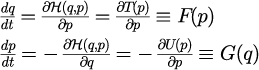
で与えられる。式(22)のは、計算アルゴリズムの見通しを良くするために導入した関数である。
時刻
の
と
を
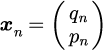
と行列で表した場合に、正準方程式を利用してから
に変換する変換則が
シンプレクティック変換と呼ばれ、
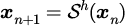
と表します。はシンプレクティック変換を表し、添字の
は時間刻み幅を表します。
は複数回の変換で
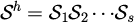
と「積」で表されます。一つ一つのは
番目のシンプレクティック変換を表す。さらに1つのシンプレクティック変換は、正準方程式に対応する2つの変換に分けられる。
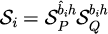
ただし、と
は
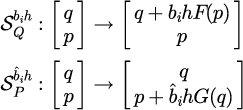
で定義される。式(26)のと
が、変換に伴う位置と運動量の変化量を表し、
の組み合わせでシンプレクティック変換に基づいた様々なアルゴリズムを構成することができる。具体的な導出例(ベルレ法との対応、4次6次の表式)[15]。
特徴
・簡単。安定。保存量が保存[15]。
・誤差の判定法が簡単。1ステップあたりの平均誤差()を計算[16]。
・誤差が最悪でも時間に比例[12]。
・物理的保存量が保存される[12]。
・欠点→時間間隔を変えると上の性質が一般的に壊れる。
・陽的:作用素文化に基づいた公式が広く使われる[12]。→ リープフロッグのタイムステップを変えて組み合わせて高次を実現
・リープフロッグは時間対称型なので、組み合わせも全て対称型となる。7段6位、15段8次も導かれている
・陽的:再帰的方法でいくらでも高次の公式を導出できるが、6次で15段、8次で27段と効率が悪い[12]
・欠点→局所誤差が悪い(ルンゲ・クッタ悪い)[12]
シンプレクティック オイラー法(1段1次)
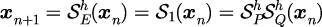
| 表 | アルゴリズム |
|---|---|
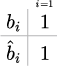 |
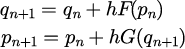 |
ベルレの方法(2段2次)
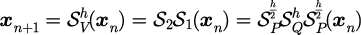
| 表 | アルゴリズム |
|---|---|
 |
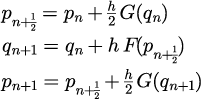 |
ベルレの方法は、単純明快で実装が簡単でかつシンプレクティック性[10]かつ時間対称型[12]を満たすため、非常に有用なアルゴリズムである。ベルレの方法と等価な方法については後述する。
さらなる陽的シンプレクティック解法も示されている。 系統的に取り扱うために、式(26)に基づいたシンプレクティック変換を
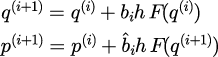
と表す。 ただし、
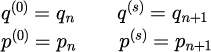
である。
ルースの公式(3段3次)
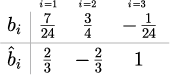
サンス・セルナの公式(6段4次)
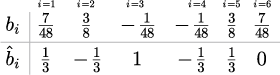
ベルレの方法
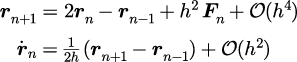
ベルレの法則は先述の通り、シンプレクティック解法の中で位置づけられるアルゴリズムであるが、 その簡便さから目的に合わせて柔軟に変更することができることから、様々なアルゴリズムが利用される。
位置ベルレの差分式
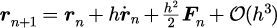
リープフロッグ差分式
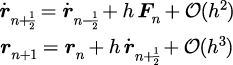
・デメリット→エネルギー保存の値の誤差が、ベルレよりも1位悪い([10])。
速度ベルレ差分式
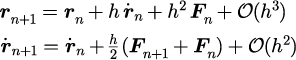
・2階微分方程式を解く際に有用[10]
・誤差:
・シンプレクティック性[10]かつ時間対称型[12]
・デメリット→時間間隔を変えられない[10]
その他のアルゴリズム
ヌメロフの公式
ヌメロフの公式は、常微分方程式が
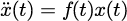
の形をしているときに、非常に効率的かつ高精度(1段階+1階+5次)なアルゴリズムとなる[10]。
元のを
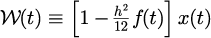
と変形することで
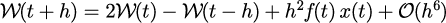
という簡単な漸化式となる。 逆変換
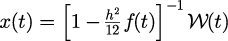
を行うことで、任意の時刻のを得ることができる。
まとめ
いろいろな文献を調べていて「シンプレクティック性、対称性、A-安定」の重要性を理解することができた。「ガウス・ルジャンドル法」は上記の条件をすべて満たすため、研究を行う上で非常に強力であると考えられる。ただし、陰的解法であるため、非線形連立方程式をニュートン法をなどで解く必要がある。
一方、陽的ルンゲ・クッタ法は上記条件をひとつも満たさないため、導入するメリット実装の容易さ以外には無いように思える。
ただし、の変動が大きな領域が存在する場合には、細心の注意が必要となる(最低でも刻み幅の自動調整が必須)。
本稿で取り上げた以外にもまだたくさんある。ブリルシュ・ストア法は、リチャードソン補外を用いて目的の精度を達成するまで反復するという手法である。それゆえ、次数という概念は存在しない。[17]の著者はこの手法が最良であると言っているほどである。しかしながら、あまり文献などで触れられていないため利用されていないようである。
数値計算の世界のディープさを少し実感することができた。
また、ITの発展に伴い、暗黙知 → 形式知 → 集合知、そして知のコモディティ化が急速に進んでいることの恩恵を受けていることも、参考文献が簡単に手に入ることで実感することができた。
自分も微力ながら、知のコモディティ化に貢献したいと思っている。
参考文献
以下の参考文献リストの並び順は、本文での出現順あるいは重要度順ではなく、全くの順不同である。強いていうならば筆者が参考にした順である。 本文中で言及されていないものも含むため注意を要す。
- [1] ニュートン・コーツの公式 - Wikipedia [WEB]
- [2] シミュレーション概論(講義ノート)[PDF](早川尚男 著)
- [3] スペクトル法による数値計算入門 [単行本](石岡圭一 著)
- [4] 統計的データ解析のための数値計算法入門 [単行本](岩崎学 著)
- [5] 二重指数関数型変換のすすめ [PDF](森正武 著)
- [6] Runge-Kutta 法についてのノート [PDF](早川尚男 著)
- [7] 陽的Runge-Kutta法のButcher tableau [WEB](330k.info 著)
- [8] Runge-Kutta5段5次型と6段6次型の実用公式 [PDF](情報処理学会論文誌、小野令美, 戸田英雄 共著)
- [9] 分子シミュレーション―古典系から量子系手法まで [単行本](上田顕 著)
- [10] 計算物理学 [単行本](J.M.ティッセン 著、松田和典, 道廣嘉隆, 谷村吉隆, 高須昌子, 吉江友照(訳))
- [11] 数学教育学習支援研究室 [WEB]
- [12] 数値計算法の基礎 [PDF](牧野淳一郎 著)
- [13] システム数理 [WEB, PDF](牧野淳一郎 著)
- [14] 計算物理学 基礎編 [単行本](Rubin H. Landau, Manuel Jose Paez Mejia (共著)、小柳 義夫, 春日隆, 狩野覚, 善甫康成 (訳))
- [15] 計算物理学特論 分子動力学シミュレーション、数値積分法 [PDF](能勢修一 著)
- [16] 分子動力学法入門 [PDF](能勢修一 著)
- [17] ニューメリカルレシピ・イン・シー 日本語版―C言語による数値計算のレシピ [単行本](William H. Press, William T. Vetterling, Saul A. Teukolsky, Brian P. Flannery (共著)、 丹慶勝市, 佐藤俊郎, 奥村晴彦, 小林誠(訳)
- [18] 分子動力学法入門 [PDF](能勢修一 著)
- [19] 「計算物理入門」~ 分子シミュレーションを中心に ~ [単行本](上田顕 著)
- [20] 計算数理特論 [PDF](三井斌友 著)Title chapter0 chapter1 chapter2 chapter3
- [21] 2段数陰的Runge-Kutta法について [PDF](情報処理学会論文誌、田中正次, 山下忠志, 山下茂 共著)
- [22] List of Runge?Kutta methods [WEB](Wikipedia)
- [23] Numerical Computation as Software [PDF](幸谷智紀 著)
- [24] 計算物理のためのC/C++言語入門 [WEB](渡辺尚貴 著)
- [25] GNU Scientific Library Guide in Japanese [WEB](幸谷智紀 著)
- [26] GSL reference manual Japanese translation [PDF](富永大介 著)
- [27] ガウス・ルジャンドル法の係数(4倍精度)[WEB](永井貴博 氏)
































