「HTML5による物理シミュレーション【拡散・波動編】」出版決定(発売日:2013年5月25日)

HTML5による物理シミュレーション【拡散・波動編】
JavaScriptライブラリとCanvas 2D Context/Web Workersを使う
著者 遠藤 理平
出版社 株式会社カットシステム
発売日 2013年5月25日
判型 B5変型判、456頁
税込価格 4,410円(本体4,200円)
ISBN 978-4-87783-312-1
最新のthree.jsで利用するために必要な変更点をまとめました:three.js仕様変更による変更点(PDF)
フジテレビ月9ドラマ【ガリレオ】HTML5による物理シミュレーション&動画の提供決定!
はじめに
本書は、HTML5を利用しウェブブラウザのみで完結した物理シミュレーション環境(仮想物理実験室)の構築手法と物理学の基礎を実践を交えながら習得することを目的とした『HTML5による物理シミュレーション』(以下『前編』と表記)の続編です。
HTML5で作成したアプリケーションは、ウェブブラウザを介して様々な環境で実行することができる上に、当然ながら、HTMLの本領であるウェブ上での公開も容易です。本書では、アプリケーションの共通プラットフォームであるHTML5の一つの応用例として、インタラクティブな新しい科学コミュニケーションツールとしての可能性を提案します。
物理シミュレーション環境の構築には、【入力】【演算】【描画】の3要素が必要となります。これまで、【入力】は各実行環境に応じたGUI、【演算】はC言語などのプログラミング言語、【描画】は二次元グラフ描写ならgnuplot、3次元グラフィックスならOpenGLというように、それぞれ独立に環境を用意し、技術を習得する必要がありました。
これに対してHTML5では、これら3要素を統一的に扱うことができ、かつ環境を別途用意する必要もなく、ウェブブラウザのみで実行可能になったことが、本書がHTML5による物理シミュレーションを提案する最大の根拠です。各ブラウザの性能が飛躍的に向上した恩恵により、これまで敷居の高かった物理シミレーションが、簡単かつ高水準で実行可能となったのです。
さらに今回、嬉しい誤算として、これまでボトルネックと考えられていた【演算】を担うJavaScriptの計算速度が、科学計算などの高速な数値計算に利用されるC言語と比べて、わずか1割程度しか遅くないことを示すことができました(詳細は本書2.3.3項を参照)。一般的にJavaScriptは、様々な形式のオブジェクトを取り扱うツールとして利用する場合、コンパイル言語と比べて処理速度が10倍ほど遅いと言われていますが、こと数値計算に限れば、C言語にも劣らない計算速度を、現ブラウザで実現できるようになったのです。
このことは、ウェブブラウザが、これまでの単なるウェブページを閲覧するためだけのツールではなく、本格的な数値計算やシミュレーションなどを実行するプラットフォームとしての性能を十分に有していることを意味します。HTML5が新しいインタラクティブな科学コミュニケーションツールとして、世界中で活躍する日も近づいているでしょう。
また、本書は『前編』とあわせることで、物理現象を理解する上で欠かせない物理量の可視化方法を、HTML5を用いて実装できる能力を習得できるよう構成されています。物理現象の多くは、常微分方程式と偏微分方程式で記述されています。常微分方程式の代表例がニュートン運動方程式、偏微分方程式の代表例が拡散方程式と波動方程式です。これらは、古典力学・電磁気学・量子力学など物理学の様々な基礎理論分野に、頻繁に登場する方程式です。
『前編』では、古典物理学の基礎である質点の運動の時間発展を二次元グラフならびに仮想3次元空間において可視化することを行いました。そして本書では、拡散現象や波動現象に対する数値計算手法の習得、ならびに物理量の空間分布に対する二次元カラーマップや二次元正方格子を用いた表現手法の習得を行います。以上の計算方法かつ描画方法の習得により、物理学の他分野にも切り込める道具を手にすることができます。
本書を通じて、HTML5の持つポテンシャルの高さをぜひ体感いただき、また、数学や物理学についての興味を持つきっかけとなれば、筆者としてこれほどの喜びはありません。なお、筆者の勉強不足のために、プログラムや数学、物理学の説明に間違いが有るかもしれません。その際はお手数ですが、ご指摘いただければ幸いです。
最後に、『前編』に引き続き本書の執筆の機会を頂きました株式会社カットシステムの石塚勝敏さん、今回も厳しいスケジュールのなか丁寧な編集を行なって頂きました株式会社チューリングの鈴木光治さん、また、日常的に議論に付き合って頂いている特定非営利活動法人natural scienceの皆さんには、深く感謝申し上げます。
2013年5月 遠藤理平
目次
- 第1章 Canvas 2D Contextによる2次元ビットマップ画像描画入門
- 1.1 Canvas 2D Contextの基本
- 1.1.1 Canvas 2D ContextとWebGL
- 1.1.2 ベクタ形式とラスタ形式
- 1.1.3 Canvas 2D Contextの準備
- 1.2 ベクタ形式による描画
- 1.2.1 直線の描画
- 1.2.2 三角形の描画
- 1.2.3 様々な形状の描画
- 1.2.4 円と円弧の描画
- 1.3 ラスタ形式による描画
- 1.3.1 矩形の描画と消去
- 1.3.2 ビットマップデータの作成と描画
- 1.3.3 ビットマップ画像の例
- 1.3.4 ラスタ形式データの取り込みと描画
- 1.3.5 ラスタ形式データの画像処理
- 1.3.6 ラスタ形式データの出力
- 1.4 Canvas 2D Contextによるアニメーション
- 1.4.1 「requestAnimationFrame()」と無限ループ
- 1.4.2 アニメーションの実装例1:「ボール跳ね返りアニメーション
- 1.4.3 アニメーションの実装例2:「ライフゲーム」
- 1.5 Cancas 2D Context メソッドとプロパティ
- 1.5.1 コンテキストのメソッド一覧
- 1.5.2 コンテキストのプロパティ一覧
- 1.5.3 イメージデータのプロパティ一覧
- 1.5.4 Imageクラスのプロパティ一覧
- 1.1 Canvas 2D Contextの基本
- 第2章 Web Workers APIによる並列計算入門
- 2.1 Web Workersの仕組みと基本形
- 2.1.1 ホストプログラムとワーカープログラム
- 2.1.2 Web Workersの基本形
- 2.1.3 ホスト・ワーカー間のオブジェクトの送受信
- 2.2 Web Workersによる並列計算
- 2.2.1 並列計算の基本概念
- 2.2.2 「2~Nまでの素数の数え上げ」アルゴリズム(ワーカーなし)
- 2.2.3 「2~Nまでの素数の数え上げ」アルゴリズム(ワーカーあり)
- 2.2.4 複数のワーカーによる並列計算アルゴリズム
- 2.2.5 ワーカー数と計算時間との関係性
- 2.3 並列計算アルゴリズムの最適化
- 2.3.1 並列計算アルゴリズムの最適化方法
- 2.3.2 Web Workersの排他制御
- 2.3.3 「JavaScript」VS「C言語」
- 2.1 Web Workersの仕組みと基本形
- 第3章 物理シミュレーション環境の構築
- 3.1 Three.js による「波動関数」&「分布関数」の表現
- 3.2.1 「replot()」メソッドによるアニメーションの実装
- 3.2.2 複数canvas要素によるアニメーションの実装
- 3.2.3 2次元グラフのPNG出力とPNGアニメーションの実装
- 3.2 jqPlot による 2次元グラフアニメーションの実装
- 3.2.1 共通インターフェースのHTMLの構造
- 3.2.2 外部CSSファイルの構造
- 3.3 アニメーション制御
- 3.3.1 ボタンによるアニメーション制御:2次元グラフ
- 3.3.2 ボタンによるアニメーション制御:2次元正方格子と2次元カラーマップ
- 3.3.3 jQuery UIによるアニメーションの制御
- 3.3.4 WebWorkersによる2次元グラフの準備
- 3.4 アニメーションビューアの開発
- 3.4.1 2次元グラフ・アニメーションビューア
- 3.4.2 2次元正方格子・アニメーションビューア
- 3.1 Three.js による「波動関数」&「分布関数」の表現
- 第4章 フーリエ級数の入門
- 4.1 べき級数展開(テーラー展開)
- 4.1.1 べき級数展開の定義
- 4.1.2 べき級数展開の例
- 4.2 フーリエ級数展開
- 4.2.1 フーリエ級数展開の定義
- 4.2.2 三角関数の直交性
- 4.2.3 展開係数の導出
- 4.2.4 フーリエ級数の完全性(中級)
- 4.2.5 フーリエ級数展開の例
- 4.2.6 フーリエ級数ビューア(FourierTransformViewer.html)
- 4.3 数値積分計算アルゴリズムの導出
- 4.3.1 数値積分の基本的な考え方
- 4.3.2 1次精度の計算アルゴリズム「矩形公式」
- 4.3.3 2次精度の計算アルゴリズム「台形公式」
- 4.3.4 4次精度の計算アルゴリズム「シンプソンの公式」
- 4.3.5 数値積分計算機(NumericalIntegralCalculator.html)
- 4.4 様々な関数のフーリエ級数展開
- 4.4.1 展開係数の数値計算方法
- 4.4.2 展開係数計算機(FourierTransformCoefficientCalculator.html)
- 4.4.3 初等関数のフーリエ級数展開
- 4.4.4 ガウス分布によるフーリエ級数展開
- 4.1 べき級数展開(テーラー展開)
- 第5章 拡散現象と拡散方程式
- 5.1 拡散方程式の導出
- 5.1.1 「ニュートンの運動方程式」と計算の限界
- 5.1.2 多粒子系→1粒子系への近似「ランジュバン方程式」
- 5.1.3 「ランジュバン方程式」から「拡散方程式」へ
- 5.2 拡散方程式の解析解と時間発展
- 5.2.1 拡散方程式の一般解
- 5.2.2 拡散方程式の解析解ビューア
- 5.2.3 拡散方程式の解析解シミュレーション
- 5.3 拡散方程式の計算アルゴリズム
- 5.3.1 拡散方程式の差分化
- 5.3.2 計算アルゴリズムの導出
- 5.3.3 初期条件と境界条件の設定
- 5.4 拡散現象の物理シミュレーション
- 5.4.1 拡散方程式の数値シミュレータ(1次元)
- 5.4.2 数値シミュレーション結果1:境界条件の違いの確認
- 5.4.3 数値シミュレーション結果2:拡散係数の空間依存性の確認
- 5.5 熱拡散シミュレーション
- 5.5.1 熱拡散シミュレータの開発
- 5.5.2 銅板の温度変化のシミュレーション
- 5.5.3 水中に置かれた銅板の温度変化のシミュレーション
- 5.1 拡散方程式の導出
- 第6章 波動現象と波動方程式
- 6.1 波動方程式の導出
- 6.1.1 波動現象とは
- 6.1.2 微小紐片の運動方程式から波動方程式へ(横波)
- 6.1.3 バネ振動子の運動方程式から波動方程式へ(縦波)
- 6.2 波動方程式の解析解と時間発展
- 6.2.1 波動方程式の基本解:平面波
- 6.2.2 波動方程式の一般解と境界条件
- 6.2.3 展開係数の計算方法
- 6.2.4 波動方程式の解析解ビューア
- 6.2.5 波動方程式の解析解シミュレーション
- 6.2.6 固定端条件における三角波シミュレーション
- 6.3 波動方程式の数値シミュレーション
- 6.3.1 波動方程式の差分化と計算アルゴリズム
- 6.3.2 波動方程式の数値シミュレータ(1次元)
- 6.3.3 波動方程式の数値シミュレータ(2次元)
- 6.4 回折・干渉・ドップラー効果のシミュレーション
- 6.4.1 波の回折現象
- 6.4.2 波の干渉現象
- 6.4.3 ドップラー効果
- 6.5 透過と反射のシミュレーション
- 6.5.1 透過係数と反射係数
- 6.5.2 入射波・反射波・透過波の描画
- 6.5.3 ガウスパルスの透過と反射【中級】
- 6.1 波動方程式の導出
付属サンプルプログラム一覧
本書で取り扱ったすべての題材にはサンプルプログラムが用意されています。
| 章 | ファイル名 | 説明 |
| 1.1.3 | canvas.html | canvas要素の基本形 |
| 1.2.1 | canvas_lines.html | 直線の描画 |
| 1.2.2 | canvas_triangle.html | 三角形の線の描画 |
| 1.2.2 | canvas_triangle_fill.html | 三角形の塗りの描画 |
| 1.2.2 | canvas_triangle_fill_stroke.html | 三角形の線+塗りの描画 |
| 1.2.3 | canvas_hexagon_fill_stroke.html | 六角形の線+塗りの描画 |
| 1.2.3 | canvas_uzamaki_stroke.html | 渦巻き図形の描画 |
| 1.2.4 | canvas_circle_fill.html | 円形の描画 |
| 1.2.4 | canvas_circle_fill2.html | 円弧の描画 |
| 1.2.5 | canvas_rect_fill.html | 矩形の描画 |
| 1.2.5 | canvas_rect_fill_clear.html | 矩形の描画+クリアーの実行 |
| 1.3.1 | canvas_bitmap_random.html | ビットマップによるランダム色の描画 |
| 1.3.2 | canvas_bitmap_gradation_linear.html | ビットマップによる線形グラデーションの描画 |
| 1.3.2 | canvas_bitmap_gradation_circle.html | ビットマップによる円形グラデーションの描画 |
| 1.3.2 | canvas_bitmap_colorModel.html | ビットマップによるRGBカラーモデルの描画 |
| 1.3.2 | canvas_bitmap_Gaussian.html | ビットマップによるガウス分布の描画 |
| 1.3.2 | Gaussian.html | jqPlotによるガウス分布の描画 |
| 1.3.2 | canvas_bitmap_planeWave.html | ビットマップによる平面波の描画 |
| 1.3.2 | canvas_bitmap_Mandelbrot.html | ビットマップによるマンデルブロ集合の描画 |
| 1.3.2 | canvas_bitmap_Mandelbrot_step.html | ビットマップによるマンデルブロ集合(発散速度によるグラデーション)の描画 |
| 1.3.3 | canvas_img.html | ビットマップ画像の取り込み |
| 1.3.3 | canvas_img2.html | ビットマップ画像の取り込み+トリミング |
| 1.3.3 | canvas_image.html | Imageクラスによる画像の取り込み |
| 1.3.4 | canvas_image_bitmap.html | 取得した画像データの色を反転して描画 |
| 1.3.4 | canvas_image_bitmap_gray.html | 取得した画像データの色をグレースケール化して描画 |
| 1.3.4 | canvas_image_bitmap_upsideDown.html | 取得した画像データの上下を逆さまにして描画 |
| 1.3.5 | canvas_image_bitmap_png.html | canvas要素の描画内容をpng形式で出力(a要素による別ウィンドウ表示) |
| 1.3.5 | canvas_image_bitmap_png2.html | canvas要素の描画内容をpng形式で出力(a要素によるダウンロード) |
| 1.3.5 | canvas_image_bitmap_png_input.html | canvas要素の描画内容をpng形式で出力(input要素によるポップアップ表示) |
| 1.3.5 | canvas_image_bitmap_png_input2.html | canvas要素の描画内容をpng形式で出力(input要素によるoctet-stream 形式ファイルのダウンロード) |
| 1.4.2 | canvas_animation.html | ボール跳ね返りアニメーション |
| 1.4.2 | canvas_animation_PBC.html | ボール跳ね返りアニメーション+周期的境界条件 |
| 1.4.3 | canvas_animation_lifeGame.html | ライフゲームシミュレーション |
| 2.1.2 | WebWorkers_test.html | WebWorkersによる1~Nまでの和の計算 |
| 2.1.2 | worker_test.js | ワーカープログラム(1~Nまでの和の計算) |
| 2.1.3 | WebWorkers_test2.html | ホストプログラムとワーカープログラム間のオブジェクトデータ送受信 |
| 2.1.3 | worker_test2.js | ワーカープログラム(オブジェクトデータ送受信) |
| 2.2.2 | prime.html | 素数の数え上げ |
| 2.2.3 | WebWorkers_prime.html | WebWorkersによる素数の数え上げ |
| 2.2.3 | worker_prime.js | ワーカープログラム(素数の数え上げ) |
| 2.2.3 | prime.js | 外部ファイル(素数判定計算) |
| 2.2.4 | WebWorkers_prime1.html | WebWorkersによる並列計算化した素数の数え上げ |
| 2.2.4 | worker_prime1.js | ワーカープログラム(並列計算化した素数の数え上げ) |
| 2.2.5 | WebWorkers_calculateTime.html | 素数の数え上げプログラムに対する計算時間のワーカー数依存性の計算+可視化(jqPlot) |
| 2.2.5 | WebWorkers_calculateTime2.html | 素数の数え上げプログラムに対する計算時間のワーカー数依存性の計算+可視化(jqPlot)(2) |
| 2.3.1 | WebWorkers_prime2.html | WebWorkersによる並列計算化した素数の数え上げの最適化 |
| 2.3.1 | worker_prime2.js | ワーカープログラム(並列計算化した素数の数え上げの最適化) |
| 2.3.1 | WebWorkers_calculateTime_optimization.html | 最適化後の素数の数え上げプログラムに対する計算時間のワーカー数依存性の計算+可視化(jqPlot) |
| 2.3.2 | WebWorkers_test3.html | WebWorkersの自動排他処理の確認 |
| 2.3.2 | worker_test3.js | ワーカープログラム(自動排他処理の確認用) |
| 2.3.3 | openMP_test.cpp | 【C言語ソース】OpenMPを利用した並列計算による素数の数え上げ |
| 3.1.1 | Quadrangle.html | Three.jsによる四角形オブジェクトの描画 |
| 3.1.2 | 2DLattice.html | Three.jsによる2次元正方格子オブジェクトの描画 |
| 3.1.3 | 2DLattice_Gaussian.html | 2次元正方格子オブジェクトによるガウス分布の描画 |
| 3.1.3 | 2DLattice_Gaussian_vertexNormal.html | 2次元正方格子オブジェクトによるガウス分布の描画+頂点法線ベクトルの設定 |
| 3.1.4 | 2DLattice_Gaussian_animation.html | 2次元正方格子オブジェクトのアニメーション |
| 3.1.5 | 2DLattice_Gaussian_animation_pre.html | 2次元正方格子オブジェクトのアニメーション(オブジェクトの事前準備) |
| 3.1.6 | 2DColormap.html | 四角形オブジェクトのカラー表示 |
| 3.1.6 | 2DColormapLattice.html | 2次元正方格子による2次元カラーマップ表示 |
| 3.1.7 | 2DColormap_Gaussian.html | 2次元カラーマップ表示によるガウス分布の描画 |
| 3.1.7 | 2DColormap_Gaussian_animation.html | 2次元カラーマップ表示のアニメーション |
| 3.2.1 | plot2D_animation_test.html | jqPlot による2 次元グラフアニメーション(replotメソッド) |
| 3.2.2 | plot2D_animation_pre.html | jqPlot による2 次元グラフアニメーション(複数canvas要素の事前準備) |
| 3.2.3 | FunctionViewer.html | 関数ビューア+pngファイル出力 |
| 3.2.3 | plot2D_animation_pre_png.html | img要素によるアニメーション |
| 3.3.1 | animationControll_plot2D.html | ボタンによるアニメーション制御(2次元グラフ) |
| 3.3.2 | animationControll_2DLattice.html | ボタンによるアニメーション制御(2次元正方格子) |
| 3.3.2 | animationControll_2DColormap.html | ボタンによるアニメーション制御(2次元カラーマップ) |
| 3.3.3 | animationControll_plot2D_UI.html | jQuery UI によるアニメーションの制御(2次元グラフ) |
| 3.3.3 | animationControll_2DLattice_UI.html | jQuery UI によるアニメーションの制御(2次元正方格子) |
| 3.3.3 | animationControll_2DColormap_UI.html | jQuery UI によるアニメーションの制御(2次元カラーマップ) |
| 3.3.4 | progressbar.html | jQuery UI によるプログレスバー |
| 3.3.4 | animationControll_plot2D_UI_workers.html | jQuery UI によるアニメーションの制御+WebWorkers(2次元グラフ) |
| 3.3.4 | worker_sin.js | ワーカープログラム(sin関数のグラフ描画データの準備) |
| 3.3.5 | animationControll_2DLattice_UI_workers.html | jQuery UI によるアニメーションの制御+WebWorkers(2次元正方格子) |
| 3.3.5 | animationControll_2DColormap_UI_workers.html | jQuery UI によるアニメーションの制御+WebWorkers(2次元カラーマップ) |
| 3.3.5 | worker_Gaussian.js | ワーカープログラム(2次元ガウス分布データの準備) |
| 3.4.1 | animationViewer_plot2D.html | 2次元グラフ・アニメーションビューア |
| 3.4.1 | worker_animation_2Dplot.js | ワーカープログラム(2次元グラフ・アニメーションデータの準備) |
| 3.4.1 | animationViewer_plot2D_rectangle.html | 2次元グラフ・アニメーションビューア(フーリエ級数による矩形関数) |
| 3.4.2 | animationViewer_2DLattice.html | 2次元正方格子・アニメーションビューア |
| 3.4.2 | animationViewer_2DColormap.html | 2次元カラーマップ・アニメーションビューア |
| 3.4.2 | worker_animation_2DLattice.js | ワーカープログラム(2次元正方格子orカラーマップ・アニメーションデータの準備) |
| 4.1.2 | TaylorExpansion_sin.html | テーラー展開の例(sin関数) |
| 4.1.2 | TaylorExpansion_cos.html | テーラー展開の例(cos関数) |
| 4.1.2 | TaylorExpansion_e.html | テーラー展開の例(exp関数) |
| 4.1.2 | TaylorExpansion_log.html | テーラー展開の例(log関数) |
| 4.2.1 | TaylorExpansion_cos_nx.html | 三角関数の周期性(cos関数) |
| 4.2.1 | TaylorExpansion_sin_nx.html | 三角関数の周期性(sin関数) |
| 4.2.4 | deltaFunction.html | sin関数によるデルタ関数の描画 |
| 4.2.4 | deltaFunction2.html | sin関数によるデルタ関数の描画2 |
| 4.2.5 | FourierTransformViewer _x.html | フーリエ級数展開によるグラフ描画(1次関数) |
| 4.2.5 | FourierTransformViewer_x2.html | フーリエ級数展開によるグラフ描画(2次関数) |
| 4.2.5 | FourierTransformViewer_rectangular.html | フーリエ級数展開によるグラフ描画(矩形関数) |
| 4.2.5 | FourierTransformViewer_step.html | フーリエ級数展開によるグラフ描画(階段関数) |
| 4.2.6 | FourierTransformViewer.html | フーリエ級数ビューア |
| 4.3.2 | Integral_rect_x2.html | 数値積分(矩形公式)で2次関数を計算 |
| 4.3.2 | Integral_rect_sin.html | 数値積分(矩形公式)でsin関数を計算 |
| 4.3.3 | Integral_trapezoidal_x2.html | 数値積分(台形公式)で2次関数を計算 |
| 4.3.3 | Integral_trapezoidal_sin.html | 数値積分(台形公式)でsin関数を計算 |
| 4.3.4 | Integral_Simpson_x2.html | 数値積分(シンプソンの公式)で2次関数を計算 |
| 4.3.4 | Integral_Simpson_sin.html | 数値積分(シンプソンの公式)でsin関数を計算 |
| 4.3.4 | Integral_x2.html | 数値積分計算アルゴリズムの比較(2次関数) |
| 4.3.4 | Integral_sin.html | 数値積分計算アルゴリズムの比較(sin関数) |
| 4.4.1 | NumericalIntegralCalculator.html | 数値積分計算機 |
| 4.4.2 | FourierTransformCoefficientCalculator.html | フーリエ級数展開係数計算機 |
| 4.4.4 | FourierTransformCoefficientCalculator_Gaussian.html | ガウス分布によるフーリエ級数展開の計算結果 |
| 5.1.1 | interaction_G.html | 重力相互作用のグラフ |
| 5.1.1 | RJpotential.html | レナード・ジョーンズポテンシャルのグラフ |
| 5.1.1 | interaction_RJ.html | レナード・ジョーンズ相互作用のグラフ |
| 5.2.2 | DiffusionEquationAnalyticalSolutionViewer.html | 【仮想物理実験室1】拡散方程式の解析解ビューア |
| 5.2.2 | DiffusionEquationAnalyticalSolutionViewer_kai.html | 【仮想物理実験室1】拡散方程式の解析解ビューア・改(WebWorkersの利用) |
| 5.2.2 | worker_coefficient.js | ワーカープログラム(フーリエ級数展開係数の計算) |
| 5.2.2 | worker_FourierSeries.js | ワーカープログラム(フーリエ級数による各時間ステップのグラフデータの計算) |
| 5.4.1 | DiffusionEquationNumericalSymulator1D.html | 【仮想物理実験室2】拡散方程式の数値シミュレータ(1 次元) |
| 5.4.3 | fermi.htm | フェルミ分布関数のグラフ |
| 5.4.3 | fermi2.htm | フェルミ分布関数による矩形関数のグラフ |
| 5.5.1 | DiffusionEquationNumericalSymulator2D.html | 【仮想物理実験室3】熱拡散シミュレータ |
| 5.5.2 | DiffusionEquationNumericalSymulator2D_1.html | 【仮想物理実験室3】熱拡散シミュレータの例(銅板に対する点熱源シミュレーション) |
| 5.5.2 | DiffusionEquationNumericalSymulator2D_2.html | 【仮想物理実験室3】熱拡散シミュレータの例(銅板に対する線熱源シミュレーション) |
| 5.5.3 | DiffusionEquationNumericalSymulator2D_3.html | 【仮想物理実験室3】熱拡散シミュレータの例(水中に置かれた銅板1枚の温度変化のシミュレーション) |
| 5.5.3 | DiffusionEquationNumericalSymulator2D_4.html | 【仮想物理実験室3】熱拡散シミュレータの例(水中に置かれた銅板2枚の温度変化のシミュレーション) |
| 6.2.1 | planeWave.html | 平面波の空間依存性のグラフ |
| 6.2.1 | planeWave2.html | 平面波の時間依存性のグラフ |
| 6.2.1 | planeWave3.html | 平面波の振幅の違いのグラフ |
| 6.2.1 | planeWaveViewer.html | 前進波と後進波の時間発展アニメーション |
| 6.2.1 | planeWaveViewer2.html | 前進波と後進波の合成波の時間発展アニメーション |
| 6.2.1 | planeWaveViewer3.html | 前進波と後進波の合成波の時間発展アニメーション2 |
| 6.2.1 | planewave2DColormap.html | 2次元平面はビューア |
| 6.2.2 | normalVibration_periodicEnd.html | 周期端における基準振動のグラフ |
| 6.2.2 | normalVibration_openEnd.html | 自由端における基準振動のグラフ |
| 6.2.2 | normalVibration_fixedEnd.html | 固定端における基準振動のグラフ |
| 6.2.4 | WaveEquationAnalyticalSolutionViewer.html | 【仮想物理実験室4】波動方程式の解析解ビューア |
| 6.2.5 | WaveEquationAnalyticalSolutionViewer_1.html | 【仮想物理実験室4】波動方程式の解析解ビューアの例(長さ1m の弦の波動現象) |
| 6.2.6 | WaveEquationAnalyticalSolutionViewer_2.html | 【仮想物理実験室4】波動方程式の解析解ビューアの例(バイオリンの弦の振動) |
| 6.3.2 | WaveEquationNumericalSymulator1D.html | 【仮想物理実験室5】波動方程式の数値シミュレータ(1 次元) |
| 6.3.2 | WaveEquationNumericalSymulator1D_1.html | 【仮想物理実験室5】波動方程式の数値シミュレータ(1 次元)の計算精度の確認 |
| 6.3.2 | WaveEquationNumericalSymulator1D_2.html | 【仮想物理実験室5】波動方程式の数値シミュレータ(1 次元)の例(ガウスパルスの伝搬) |
| 6.3.3 | WaveEquationNumericalSymulator2D.html | 【仮想物理実験室6】波動方程式の数値シミュレータ(2 次元) |
| 6.3.3 | WaveEquationNumericalSymulator2D_1.html | 【仮想物理実験室6】波動方程式の数値シミュレータ(2 次元)点波源の与え方 |
| 6.3.3 | WaveEquationNumericalSymulator2D_2.html | 【仮想物理実験室6】波動方程式の数値シミュレータ(2 次元)線波源の与え方 |
| 6.4.1 | WaveEquationNumericalSymulator2D_diffraction.html | 【仮想物理実験室6】波動方程式の数値シミュレータ(2 次元)の例(回折現象シミュレーション) |
| 6.4.2 | WaveEquationNumericalSymulator2DColormap.html | 【仮想物理実験室6】波動方程式の数値シミュレータ(2 次元・カラーマップ)の例(点波源による干渉シミュレーション) |
| 6.4.2 | WaveEquationNumericalSymulator2DColormap_diffraction.htm | 【仮想物理実験室6】波動方程式の数値シミュレータ(2 次元・カラーマップ)の例(2重スリットによる干渉シミュレーション) |
| 6.4.3 | WaveEquationNumericalSymulator2DColormap_Doppler.html | 【仮想物理実験室6】波動方程式の数値シミュレータ(2 次元・カラーマップ)の例(ドップラー効果) |
| 6.5.2 | transparentViewer.html | 入射波・反射波・透過波アニメーション |
| 6.5.3 | transparentPulseViewer.html | ガウスパルスの透過と反射アニメーション |
サンプルプログラム実行例(画面キャプチャ)
第1章
ビットマップによるRGBカラーモデルの描画
ビットマップによるマンデルブロ集合(発散速度によるグラデーション)の描画
第2章
素数の数え上げプログラムに対する計算時間のワーカー数依存性の計算+可視化(jqPlot)
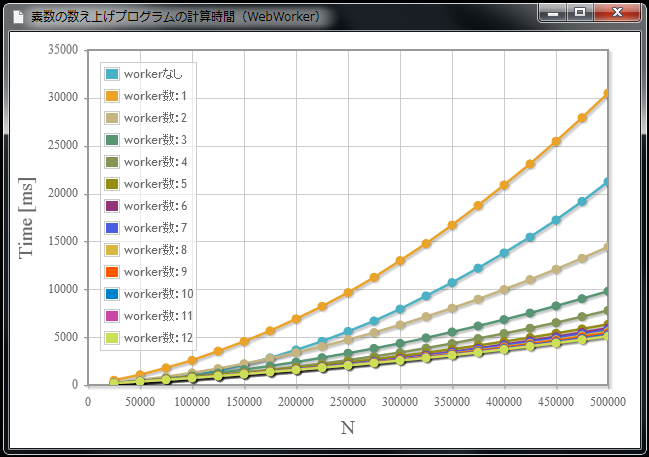
第3章
2次元正方格子による2次元カラーマップ表示
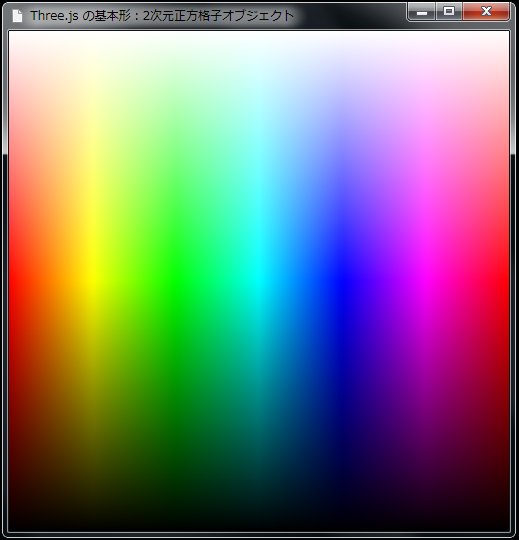
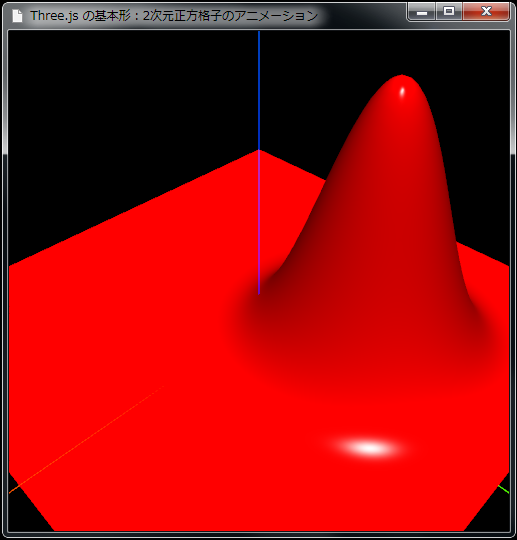
2次元正方格子・アニメーションビューア
第4章
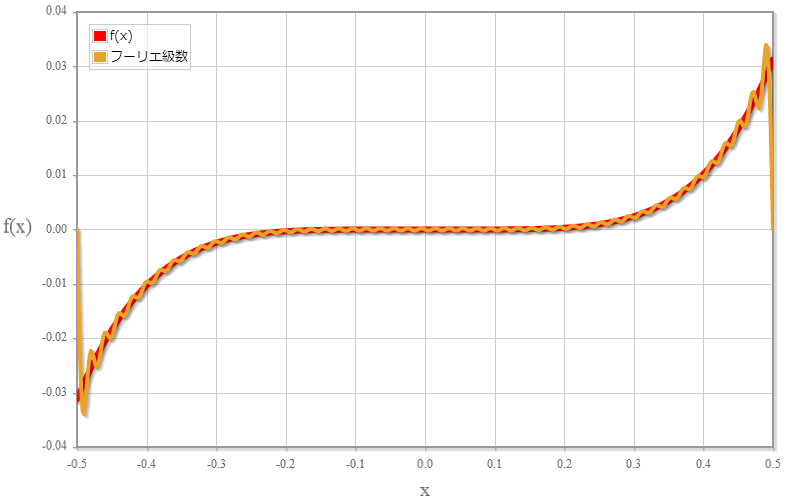
フーリエ級数ビューア
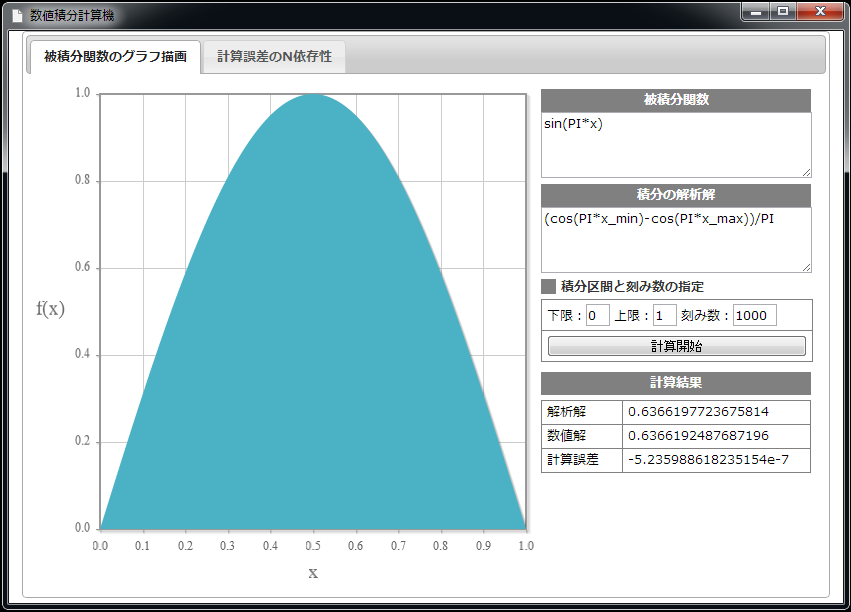
数値積分計算機
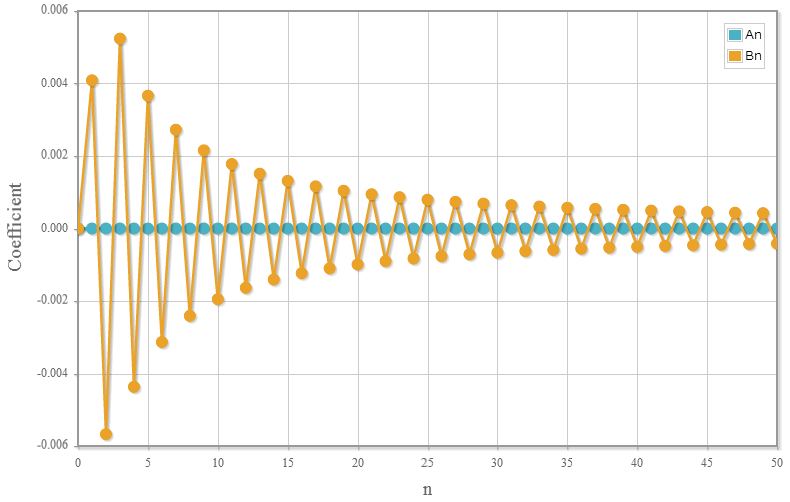
フーリエ級数展開係数計算機
第5章
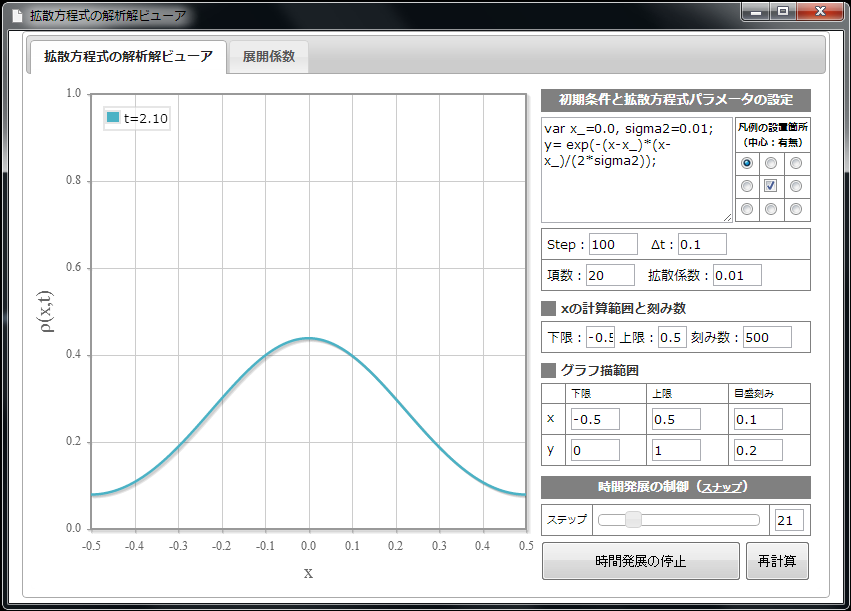
【仮想物理実験室1】拡散方程式の解析解ビューア

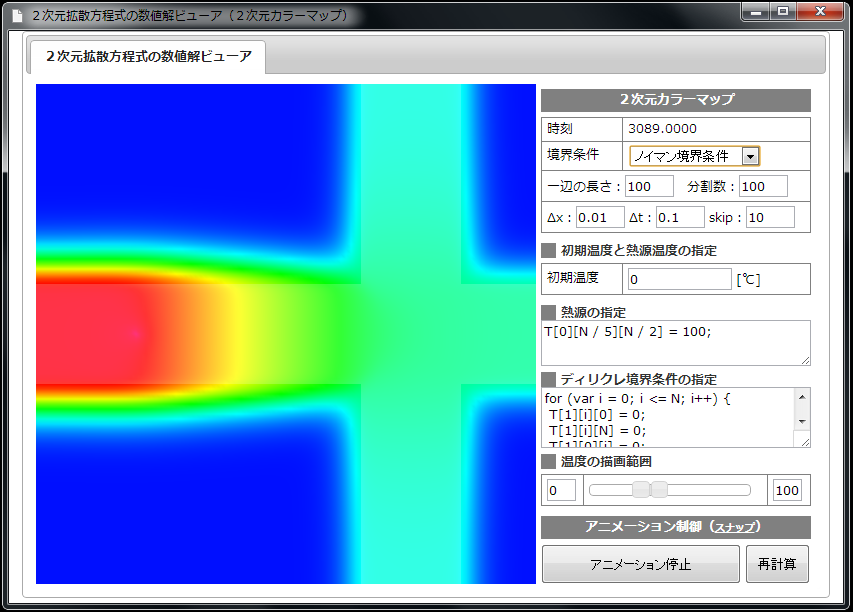
【仮想物理実験室3】熱拡散シミュレータ
第6章
【仮想物理実験室4】波動方程式の解析解ビューアの例(バイオリンの弦の振動)
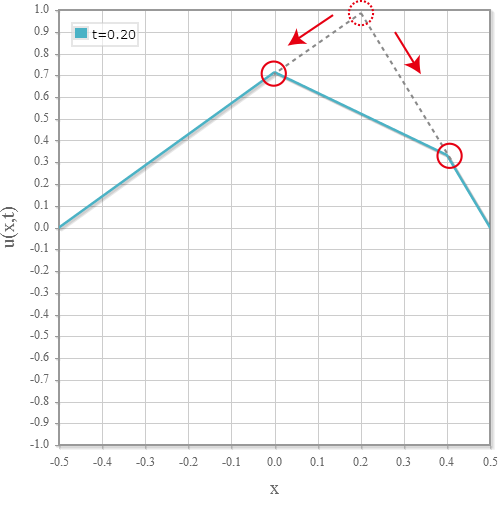
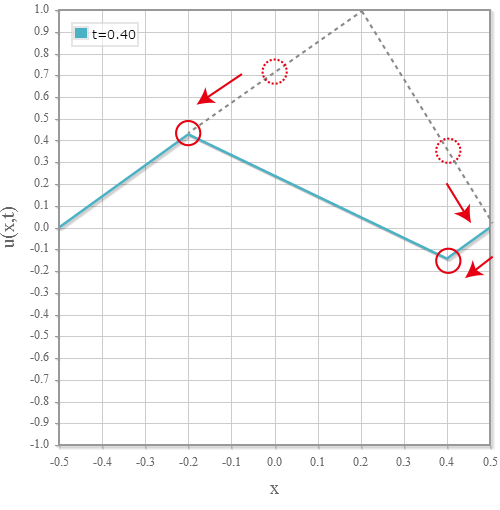
【仮想物理実験室6】波動方程式の数値シミュレータ(2 次元)
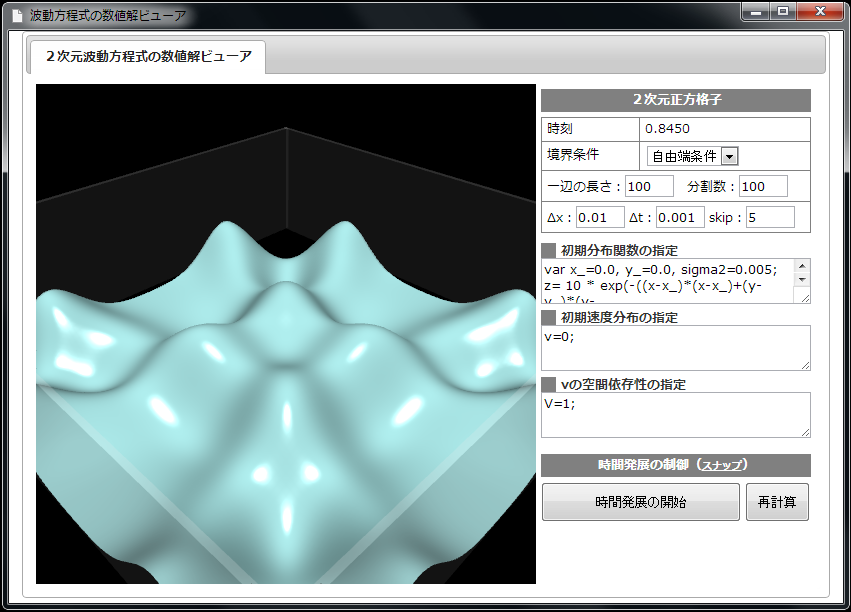
【仮想物理実験室6】波動方程式の数値シミュレータ(2 次元)の例(回折現象シミュレーション)

【仮想物理実験室6】波動方程式の数値シミュレータ(2 次元)の例(点波源による干渉シミュレーション)

【仮想物理実験室6】波動方程式の数値シミュレータ(2 次元)の例(ドップラー効果))

最後に実際に動作するデモを紹介します
WebGLに対応したウェブブラウザでご覧ください → 波動方程式による時間発展(ノイマン境界条件)