HTML5による有限要素法に基づいた2次元弾性体変形シミュレーション 第2回
第1回 メッシュのデータ構造とCanvas要素による描画
第2回 Numeric.jsによる線形代数
第3回 変形の表現と境界条件
第4回 全体剛性マトリクスの組み立てと剛性方程式の求解
第2回では有限要素法(FEM)の実装に必要となる線形代数演算の実現について解説します。 線形FEMは対象物の形状や材料特性をもとに大きな連立一次方程式を組み立てます。 連立一次方程式の解法を実装することは比較的煩雑で、 十分な知識がないと膨大な計算時間を必要とする効率の悪いものになってしまいます。 本記事ではJavascriptの線形代数ライブラリNumeric Javascript (Numeric.js) を用いることで簡単に高性能な線形代数演算を実現する方法を説明します。 線形代数演算をライブラリに任せることでFEMの実装ステップに集中することができます。
Numeric.jsの概要
Numeric.jsはjavascriptで数値計算を 行うための高性能な数値計算ライブラリです。 現在(2013/11/2)の最新バージョンは1.2.6で、線形代数、複素数、スプライン補間、微分方程式、最適化、偏微分方程式、疎行列演算に対応しています。 開発者によって行列演算を提供するほかのライブラリ(Sylvester, Google Closure's Matrix object)との比較ベンチマークが行われており、Numeric.jsがほとんどの場合で最も優れた結果を出しています。 本記事では線形代数関係のライブラリを用います。
Numeric.jsの使い方
準備
こちらのDOWNLOADSからnumeric-1.2.6.min.jsをダウンロードします。
HTMLファイルでは以下のようにnumeric.jsを読み込みます。
<script type="text/javascript" src="numeric-1.2.6.min.js"></script>
HTMLファイルの全体はたとえば以下のようになります。
<!doctype html>
<html>
<head>
<meta charset="utf-8">
<title>Numeric Javascriptの練習</title>
<!-- jquery -->
<script type="text/javascript" src="http://ajax.googleapis.com/ajax/libs/jquery/1/jquery.min.js"></script>
<!-- numeric javascript -->
<script type="text/javascript" src="numeric-1.2.6.min.js"></script>
<!-- 自分のjavascriptコード -->
<script type="text/javascript">
// HTMLを読み終わった後に実行する関数
$(document).ready(function() {
// ここにJavaScriptのコードを書く
});
</script>
</head>
<body>
</body>
</html>
DocumentとWorkshopの活用
Numeric.jsのwebサイトでは簡潔なドキュメントが用意されています。 それほど膨大なライブラリではないのでドキュメントを読めば使い方をすぐに確認できます。 また、Numeric.jsの実行結果を対話的に試すことができるWorkshopが用意されています。 式を入力すると評価結果がすぐに出力されるので使い方の確認に便利です。 これからNumeric.jsの実際の記述方法を述べますが、上のようなHTMLファイルを作成してJavascriptのコードを記述しても、 Workshopに打ち込んでも実行結果を確認することができます。
ベクトル演算
Numeric.jsではベクトルや行列をArrayクラスでのインスタンスで表現します。 ベクトルの初期化や演算は以下のような方法で行うことができます。 なお、ベクトル・行列のコピーを行うために代入演算子を使うと参照のコピーとなってしまいます。 必ず下記のようにnumeric.clone()を使うようにすべきです。
// ベクトルの初期化 Arrayクラスの初期化
var a = [0,1,2,3,4,5];
console.log("a = " + a);
// ベクトルの初期化 線形空間メソッドを使った初期化
var b = numeric.linspace(0,10,6);
console.log("b = " + b);
// ベクトルのコピー
var c = numeric.clone(a);
console.log("c = " + c);
// ベクトルの足し算
c = numeric.add(a, b);
console.log("a+b = " + c);
// ベクトルの引き算
c = numeric.sub(a, b);
console.log("a-b = " + c);
// ベクトルとスカラーの積
c = numeric.mul(2, a);
console.log("2*a = " + c);
// ベクトルの要素同士の積
c = numeric.mul(a, b);
console.log("a[i]*b[i] = " + c);
// ベクトルとスカラーの割り算
c = numeric.div(a, 2);
console.log("a/2.0 = " + c);
// ベクトルの要素同士の割り算
c = numeric.div(a, b);
console.log("a[i]/b[i] = " + c);
// ベクトルの内積
c = numeric.dot(a, b);
console.log("a*b = " + c);
// ベクトルのノルム
c = numeric.norm2(a);
console.log("|a| = " + c);
実行するとコンソールに次のような結果が得られます。
"a = 0,1,2,3,4,5" "b = 0,2,4,6,8,10" "c = 0,1,2,3,4,5" "a+b = 0,3,6,9,12,15" "a-b = 0,-1,-2,-3,-4,-5" "2*a = 0,2,4,6,8,10" "a[i]*b[i] = 0,2,8,18,32,50" "a/2.0 = 0,0.5,1,1.5,2,2.5" "a[i]/b[i] = NaN,0.5,0.5,0.5,0.5,0.5" "a*b = 110" "|a| = 7.416"
行列演算
行列の初期化は以下のように行います。
// 行列の初期化 Arrayクラスの初期化
var a = [[0,1],[2,3]];
var b = [[2,1],[3,0]];
console.log("a = " + a);
console.log("b = " + b);
// すべて同じ要素の行列作成
var c = numeric.rep([2,3],2);
console.log("rep([2,3],2) " + c);
// ランダムな要素の行列作成
c = numeric.random([2,3]);
console.log("random([2,3]) " + c);
// 対角行列を作成
c = numeric.diag([1,2,3]);
console.log("diag([1,2,3]) " + c);
実行結果は以下のようになります。 なお、サンプルコードでは2次元配列が第1行から区切りなしに1次元的に出力されます。 結果の確認はWorkshopを用いた方がわかりやすいので、そちらで実行することをお勧めします。
"a = 0,1,2,3" "b = 2,1,3,0" "rep([2,3],2) 2,2,2,2,2,2" "random([2,3]) 0.9576325253924044,0.2284188680824243,0.3651753075679791,0.47908038514161366,0.5157552174009359,0.8310511388326021" "diag([1,2,3]) 1,0,0,0,2,0,0,0,3"
次に各種演算の例を示します。
// 行列の初期化 Arrayクラスの初期化
var a = [[0,1],[2,3]];
var b = [[2,1],[3,0]];
console.log("a = " + a);
console.log("b = " + b);
// 行列のコピー
c = numeric.clone(a);
console.log("clone(a) = " + c);
// 行列の足し算
c = numeric.add(a, b);
console.log("a+b = " + c);
// 行列の引き算
c = numeric.sub(a, b);
console.log("a-b = " + c);
// 行列とスカラーの積
c = numeric.mul(2, a);
console.log("2*a = " + c);
// 行列の要素同士の積
c = numeric.mul(a, b);
console.log("a[i]*b[i] = " + c);
// 行列とスカラーの割り算
c = numeric.div(a, 2);
console.log("a/2.0 = " + c);
// 行列の要素同士の割り算
c = numeric.div(a, b);
console.log("a[i]/b[i] = " + c);
// 行列の転置
var d = numeric.transpose(b);
console.log("transpose(b) = " + d);
// 行列の積
c = numeric.dot(a, b);
console.log("a*b = " + c);
実行結果は以下の通りです。
"a = 0,1,2,3"
"b = 2,1,3,0"
"clone(a) = 0,1,2,3"
"a+b = 2,2,5,3"
"a-b = -2,0,-1,3"
"2*a = 0,2,4,6"
"a[i]*b[i] = 0,1,6,0"
"a/2.0 = 0,0.5,1,1.5"
"a[i]/b[i] = 0,1,0.6666666666666666,Infinity"
"transpose(b) = 2,3,1,0"
"a*b = 3,0,13,2"
行列式、逆行列の計算は以下の通りです。
// 行列式
var a = [[0,1],[2,3]];
console.log("a = " + a);
var det = numeric.det(a);
console.log("det = " + det);
// 逆行列
var ainv = numeric.inv(a);
console.log("ainv = " + ainv);
console.log("a*ainv = " + numeric.dot(a,ainv));
実行結果は以下のようになります。
"a = 0,1,2,3"
"det = -2"
"ainv = -1.5,0.5,1,0"
"a*ainv = 1,0,0,1"
連立一次方程式
連立方程式は行列を用いて次のように記述されます。
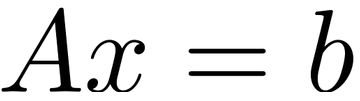
ここで, Aはn×nの行列, x, bはn次元ベクトルで、A, bは既知、xは未知です。
未知数であるxを得るためには両辺に逆行列を掛けます。
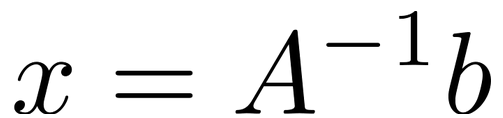
しかし逆行列の計算は非常に計算量が多いため、逆行列を何度も呼び出すような状況でなければ行うべきではありません。
Numeric.jsはLU分解に基づいた連立方程式の求解を提供しています。
x = numeric.solve(A, b);
numeric.solveの使用例を以下に示します。
var A = [[1,3],[4,7]];
var b = [5,3];
var x = numeric.solve(A, b);
var tmp = numeric.dot(A, x);
tmp = numeric.sub(tmp, b);
console.log("A = " + A);
console.log("b = " + b);
console.log("x = " + x);
console.log("A*x-b = " + tmp);
実行結果は以下の通りです。
"A = 1,3,4,7"
"b = 5,3"
"x = -5.2,3.4"
"A*x-b = -8.881784197001252e-16,0"
Numeric.jsはこのほかにも固有値、固有ベクトルの計算や特異値分解、疎行列の関数を提供しています。 今回実装するFEMでは基本的な行列計算と連立一次方程式の求解ができれば済みます。 これらの使い方はドキュメントを参照してください。
第1回 メッシュのデータ構造とCanvas要素による描画
第2回 Numeric.jsによる線形代数
第3回 変形の表現と境界条件
第4回 全体剛性マトリクスの組み立てと剛性方程式の求解























