「physics.js」による仮想物理実験室
クーロン力によるポテンシャルエネルギーの３次元表示モード～ラザフォード散乱実験シミュレーション～

はじめに

　本項物理シミュレーション環境構築用HTML5フレームワーク「physics.js」を用いて物理シミュレーションを行うための手順をチュートリアル形式で紹介する記事です。 最新版「physics.js」（リビジョン14、2017年04月05日現在）をここからダウンロードしてください。以下はチュートリアルの目次です。

• １. 仮想物理実験室のつくりかた
• ２. ３次元オブジェクトを配置しよう！
• ３. 球体を運動させてみよう！～運動の有無・位置・速度の与え方～
• ４. 球体に重力を与えよう！～一定力の与え方～
• ５. 球体を床面に衝突させよう！～衝突相互作用の与え方～
• ６. 球体を回転運動させよう！～角速度の与え方～
• ７. 球体に空気抵抗を与えよう～抵抗力の与え方～
• ８. 運動する球体同士の衝突～衝突相互作用の与え方２～
• ９. 球体を単振動運動させよう！～線形ばね相互作用の与え方～
• 10. 球体を単振子運動させよう！～２点間距離固定拘束力の与え方～
• 11. 球体を楕円軌道運動させよう！～万有引力相互作用の与え方～
• 12. 万有引力によるポテンシャルエネルギーの３次元表示モード～ポテンシャルエネルギーの可視化方法～
• 13. 万有引力相互作用で円軌道運動をさせるための初速度の与え方
• 14. クーロン力で点電荷を運動させよう！～クーロン相互作用の与え方～

小技

• ・GIFアニメーションの生成／出力の方法
• ・プレ計算モードの設定方法

３次元オブジェクト

• ・Floorクラス（床オブジェクト）
• ・Axisクラス（軸オブジェクト）
• ・Planeクラス（平面オブジェクト）
• ・Circleクラス（円オブジェクト）
• ・Boxクラス（箱オブジェクト）
• ・Cylinderクラス（円柱オブジェクト）
• ・Lineクラス（線オブジェクト）
• ・Pointクラス（点オブジェクト）
• ・Polygonクラス（ポリゴンオブジェクト）
• ・地球オブジェクト（Earthクラス）
• ・Surfaceクラス（曲面オブジェクト）

クーロン力によるポテンシャルエネルギー

「クーロン力で点電荷を運動させよう！～クーロン相互作用の与え方～」では、 クーロン力による荷電粒子の運動のシミュレーション方法を解説しました。クーロン力も万有引力と同様にポテンシャルエネルギーを定義することができ、z軸成分をポテンシャルエネルギーの大きさとして表現することができます。
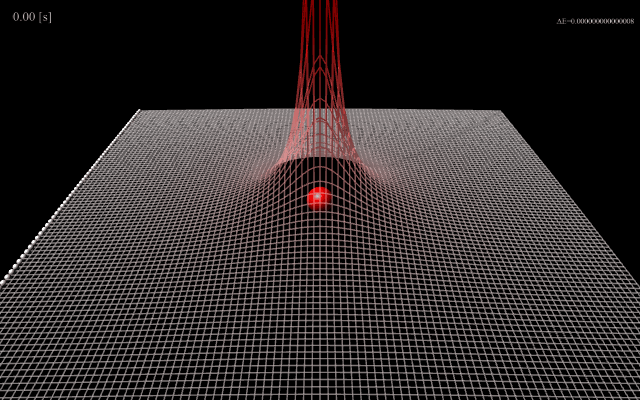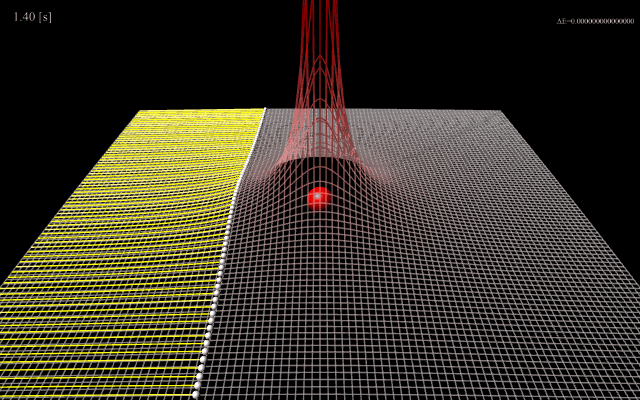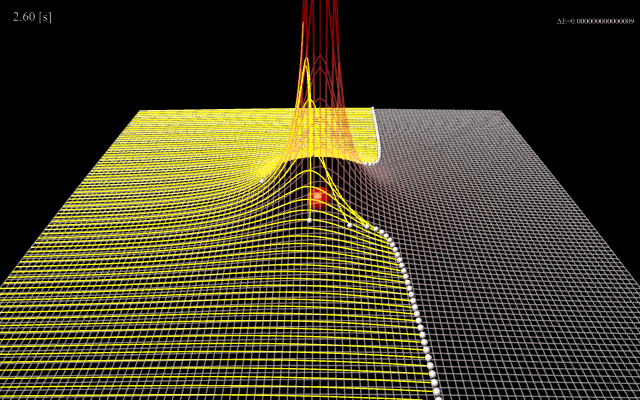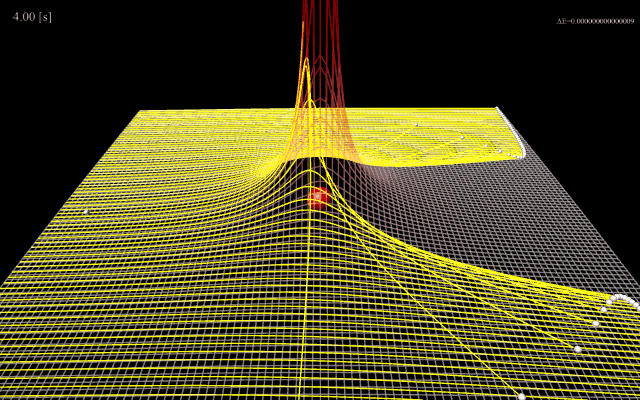
図１は中心に配置した質量の大きな正電荷の荷電粒子に向かって質量の小さな電荷粒子を照射したシミュレーション結果です。 照射する荷電粒子の電荷量、質量、初速度によって軌道の曲がり方が異なり、軌道の様子から中心電荷量を見積もることができます。 これはラザフォード散乱実験と呼ばれます。

（図１）中心の荷電粒子によるポテンシャルエネルギー（GIFアニメーション）

■実際の仮想物理実験室はこちら

ポテンシャルエネルギーの可視化

ポテンシャルエネルギーを表す格子オブジェクトはpotential3DModeプロパティの各プロパティにパラメータ与えることで生成することができます。 enabledプロパティにtrueを与えると、３次元オブジェクトのz値はポテンシャルエネルギーの値となります。 noGraphicsプロパティにtrueを与えると、可視化のためのポテンシャルエネルギーを表す格子オブジェクトは生成しません。 visibleプロパティは格子オブジェクトの表示の有無を指定します。 potentialFunctionプロパティはxy平面上におけるポテンシャルエネルギーの大きさ（z値）を与える関数を指定します。３次元オブジェクトのz値もこの値になります。 positionFunctionプロパティは格子オブジェクトの位置を与える関数を指定します。 colorFunctionプロパティは格子の頂点色を与える関数を指定します。
次のプログラムソースは、図１のラザフォード散乱実験シミュレーションを行うための１個の中心荷電粒子と８０個の照射する荷電粒子に対してpotential3DModeプロパティを与えています。

【プログラムソース１】ポテンシャルエネルギーの可視化例（RutherfordScattering.html）

//粒子数
var N = 80;
for( var i=0; i<N+1; i++  ){

	PHYSICS.physLab.balls[ i ] = new PHYSICS.Sphere({
		（省略）
		//ポテンシャルエネルギー表示モード
		potential3DMode : {
			enabled : (i!=0)? true : false,    //中心の荷電粒子のみ利用無し
			noGraphics : (i==1)? false : true, //1番目の粒子以外はグラフ表示無し
			visible : true,
			//ポテンシャルの関数形
			potentialFunction : function( x, y, parameter ){
				var max = 20;
				var core = PHYSICS.physLab.balls[ 0 ];
				var R2 = PHYSICS.Math.getLengthSq( core.position, {x:x, y:y, z:0} );
				var U = ( R2 != 0 )? 15/Math.sqrt( R2 ) : 15/Math.sqrt( 0.001 );
				return (Math.abs(U)<max)? U : max*U/Math.abs(U);
			},
			//ポテンシャル表示位置
			positionFunction : function( ){
				var core = PHYSICS.physLab.balls[ 0 ];
				return { x:core.position.x, y:core.position.y, z:core.position.z-2 };
			},
			//ポテンシャルの頂点色
			colorFunction : function( x, y, z, parameter ){
				var core = PHYSICS.physLab.balls[ 0 ];
				var R2 = PHYSICS.Math.getLengthSq( core.position, {x:x, y:y, z:0} );
				var w = +1.0/Math.sqrt(R2);
				var R = 1;
				var G = 1 - w;
				var B = 1 - w;
				return { r: R, g: G, b: B };
			},
			n : 100,    //一辺あたりの格子数
			width :0.4, //格子の一辺の長さ
			color: 0xFFFFFF,
			opacity: 0.5 //透明度
		},
	（省略）
	});
}