万華鏡について

教養学部情報科学科　３年 結城　麻衣

実験目的

万華鏡は、誰もが一度は見たことのある玩具の一つだと思います。円筒で、穴から中を見ると不思議な模様が一面に広がっていて、筒を回すと瞬く間に模様が変わっていくのを楽しむ玩具です。実に綺麗で魅了されますが、実際何故不思議な模様が広がるのでしょうか？その疑問を解く為、実験をしました。

仮説

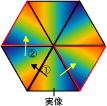万華鏡は名前のとおり、鏡で模様を無限に作り出しているのはわかります。万華鏡を覗き込むと、真正面に映し出す実物の三角形が見えます。右の図のように、その三角形を中心に、左の鏡で考えると、まず最初に実物を映し（図の①）、さらにそれを映す右の鏡も映し出し、それの繰り返すことで模様がどんどん広がっていくと思われる。

結果

万華鏡の中の構造は、3枚の長方形型の鏡板を三角柱状に組み、底面に映し出される像を鏡が反射を繰り返し映し出すことで、あの模様ができています。まず、調べるに当たって万華鏡の源である、鏡の反射ついて調べてみました。

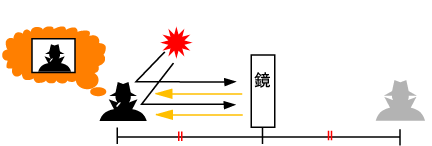
物は、光を反射することで、光が目に届き物を確認することができます。それと同様で、鏡も人が光を反射し、その光が鏡によって跳ね返ってくることで目に届き、自分の姿が見えるという仕組みになっています。映った姿は、自分と鏡の距離と同じくらい離れた場所にいるように映りますが、もちろんその先には何もありません。

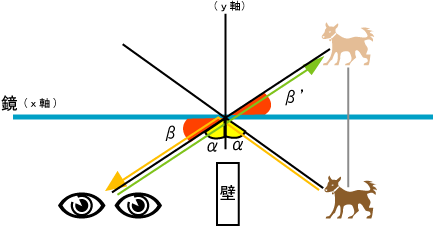
鏡を真正面から見た時、光はまっすぐ反射し自分が見えますが、実物は見えないのに、鏡の奥にいるように見えることがあります。それも反射によって見える現象ですが、反射する光の入射角と反射角は等しいという反射の法則があります。鏡に反射し、目に光が届き、目は反射した光の延長線上と、物体の鏡（ｘ軸）に対する直角な線とぶつかったところに、あたかも実物があるように見えるように感じます。∠βは対頂角なので、∠β＝∠β'になります。

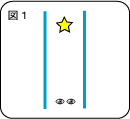では、図１のように物を合わせ鏡の間に置き、少し離れた位置から見たとき、どのように見えるでしょうか？まず、上で述べたように左右の一回反射して、目に届くので、左右に実物と鏡と同じ距離離れた先にそれぞれ見えます。次に、反射の法則は入射角が同じことが前提なので、一度右の鏡に反射して、さらに左の鏡に反射して目に光が届くということも可能です。そうなると、左右の反射角が同じであれば、問題なく反射した像が見えるので、永遠に映像が見えることになります。

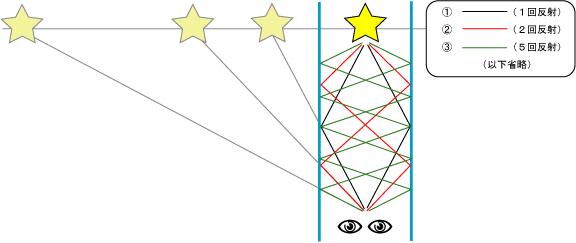
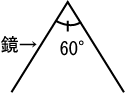万華鏡も同様の原理で成り立っています。鏡を２枚使って６０°の合せ鏡で考えて見ましょう。
反射１回は、そのまま鏡に反射して目に届きます。反射２回は、左の鏡に映ったら鋭利なほうに反射し、反対側の鏡に反射して目に届きます。このような感じに、先ほどと同様に繰り返していくと下のような図ができます。実像の真向かいに当たる像は、左右の反射がちょうどかぶり、半分ずつ映し合っている状態になっています。

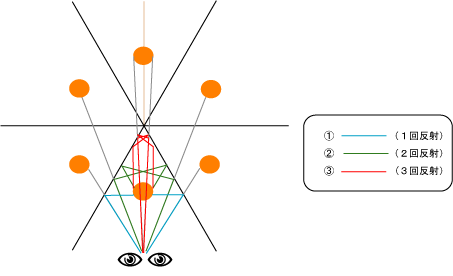
目の部分を鏡に置き換えると正三角形になり、その面にはそのまま同様の模様が映ります。 よって、反射を繰り返すことであの不思議な模様ができあたるのです。

今後の課題

・正三角形以外の三角形だとどのような模様になるのか。