人の認識---視覚追従実験---

私たちは五感で刺激をうけ、それに対して反応している。
五感のうち、視覚情報が約7割を占めているという。今回は、五感の中の視覚に注目する。
情報となる刺激は外界から得られるものだ。
それが人間の内部で統合・処理される。
そして、それをもとに外界へと何らかの反応をする。
この刺激を受けて反応するまでの過程において「認識」が重要であると私は考える。
受けた刺激に対する認識のしかたの違いによって反応が異なると考えられるからだ。
視覚刺激の知覚、つまり、何を見たのかというのは共有することができる、客観的なものである。
しかし、それをどのように見たのかという認識については共有することが難しい、いわば主観的なものである。
そして、その主観を通して出てくるのが反応であり、反応は外界に対して行われる、共有可能な客観的な ものとしてみることができる。
では、共有可能な客観的な世界から、共有が困難な主観的世界を知ることができないだろうか。
これが人の認識を考えるうえで明らかにしたいと考えるところである。

視覚追従実験

視覚追従実験とは

視覚情報において、光刺激が入力としてあり、そしてそれを基にした反応がある。 しかし、入力を受けてから、それが処理、統合され、知覚、または認識されるまでには、わずかだが時間がかかる。 その時間差を埋め、現在の外界の状況に合った反応をするために、わたしたちの脳は外界がどれだけ変化するかを脳が予測して わたしたちに知覚させているという。しかし、この予測がどのようにしてなされているのかについて不明な点は多いようだ。
この、視覚追従実験では、「等速で円運動をする物体をマウスで、できるだけ正確に追いかける」という課題に対する 人間の反応から予測メカニズムを明らかにしようとするものだ。
現時点で、リズムを生んでターゲットを追いかけることと、ターゲットに対する先行性が結果として表れているようだ。 （「リズム」、「先行性」などの定義は以下）

研究の背景・目的

最初の印象としては、リズムをもってターゲットを追いかけているというのは、円運動をするときの手の動きによってリズムが 現われているのではないかと思った。しかし、まず、リズムというのが何を示すのかということが分からない。 まずは、視覚追従実験がどのような実験で、そして結果をどのように見るのかを学んでいこうと思う。

実験方法

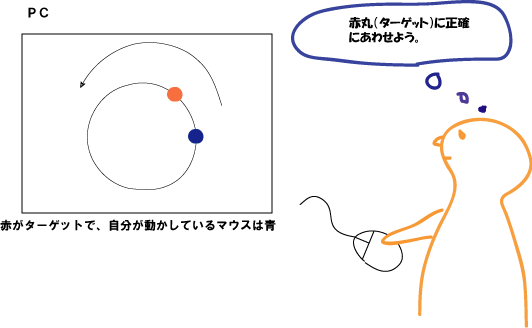
動く物体（ターゲット）を人間（マウス）が追いかける。 その際、できるだけ正確に合わせるようにしてもらう。

1.ターゲットは半径6.5cmの円の円周上を一定の速度で動く
2.ターゲットの速度は0.1Hz～0.7Hz
3.一回の実験は30秒間で、各周波数ごとに10回ずつ行う
4.赤丸がターゲットで、青丸がマウス

実験結果の解析方法―位置の差

実験結果からターゲットとマウスの位置の差を見る。まずは、位置情報をどのように処理しているのかを述べ、次にそこの何に着目したのかを言葉を与えて定義する。
0.02秒に一回、マウスの位置からターゲットの位置を引いた、位置の位相差をとっており、単位はラジアンである(図２左)。 例えば、一回目のサンプル結果が0.2、二回目が0.4、三回目が0.2、四回目が0、五回目が－0.2、六回目が－0.4だったとすると、図２の右のようになる。

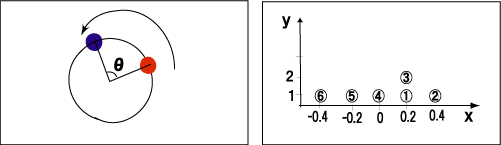
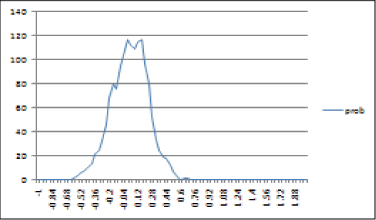
図３は実際の実験結果である。ｘ軸がマウスの位置からターゲットの位置をひいたもので、ｙ軸が回数である。サンプル回数は0.02秒に一回で、30秒間の実験なので、1500回である。

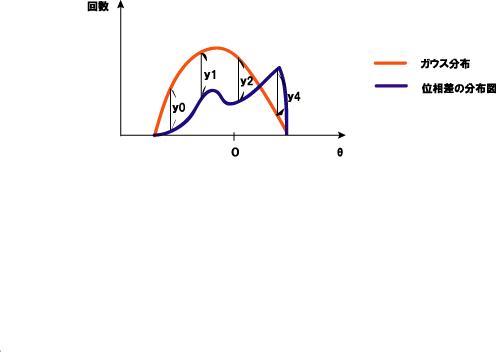
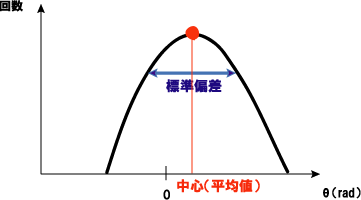
これをガウス分布にフィッティングする。ガウス分布というのは、○○○である。 そして、フィッティングというのは、元のデータを、最も近い値の状態でガウス分布にすることだ。 元の分布図と、様々な大きさのガウス分布を比べ、元のデータの値に最も近いガウス分布を見つけ出す。 ｘ座標が同じときの位相差の分布図のｙ軸の値と、ガウス分布のｙ軸の値の差分をとり、それを絶対値にする。 その絶対値の合計が最も小さくなるガウス分布にすることがフィッティングである。 簡単にだが、図で表すと、図４のようなイメージである。あるx座標における位相差の分布図と、ガウス分布の、y軸の差分$y_0$、$y_1$、$y_2$、$y_3$ があり、これらの絶対値の合計が最小となるガウス分布を探している。\\

そして、このガウス分布から、本実験で使用する言葉の定義を行う。
1. 正確さ（中心）...ガウス分布の中心のｘ軸の値（平均値）。図５
2. 標準偏差...データの62％が入る幅の大きさ。精密度ともいい、測定値のばらつきを示す。図５
3. 先行...中心が0よりも大きい場合
4. 後行...中心が0よりも小さい場合

実験結果の解析方法―速度の差

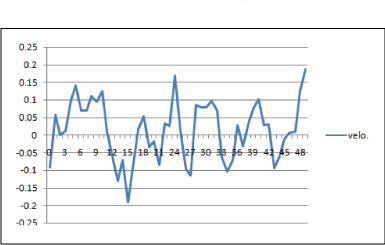
マウスはターゲットをどのように追いかけていたのかを、速度の差の実験結果から導きたい。 図6はマウスの速度とターゲットの速度の差を時間ごとにみた、速度の時系列である。 x軸はサンプルの回を示し、ｙ軸はマウスの速度からターゲットの速度を引いた差である。 実際は300回サンプルしたが、図\ref{timescale}では見やすくするため、サンプル数50回目までを表示した。

ここから、マウスがどのようにしてターゲットを追いかけているのか知りたいのだが、図６を見てわかるとおり、 なんのことやらわからない。これを、フーリエ変換する。
さて、フーリエ変換とは何か。 これは現在勉強中のため、とりあえず、周期的な成分がどれだけ含まれているかを抜き出すものと考える。
速度の時系列をフーリエ変換したものが図７である。 これをみると、ターゲットと同じ周波数（ｆ）と、その二倍の周波数（2ｆ）で強いピークが出る。 さて、これは何を意味するのだろうか。 たとえば、ｆの場合、これは、ターゲットが一周する間に、ターゲットに対して「速く動かす」→「遅く動かす」 （または、「遅」→「速」）というマウスの動かし方をしていることになる。 (2fの場合はターゲットが一周する間に「速」「遅」「速」「遅」、または、「遅」「速」「遅」「速」と動かしていることになる)。

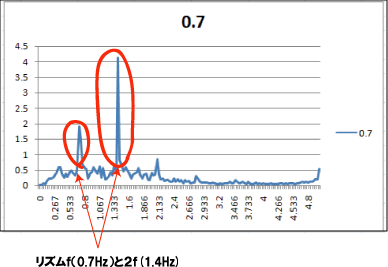
これらの動かし方が顕著である。 つまり、これはターゲットを追いかける際の大きな動きと考えることができる。これが現時点でのリズムの定義である。
リズムの実験結果としては、0.1Hz、0.2Hzの、ターゲットの速度が遅い場合はリズムは見られなかった。 0.3Hzからは、周波数が高くなるにつれて、リズムも強くなる傾向にあるという実験結果が得られた。
ターゲットを追いかける大きな動きをリズムとしたわけであるが、「ターゲットに正確に合わせる」ためには、 当然、ターゲットとマウスの位置を合わせるための細かい動きが必要である。 この動きを補正とする。では、補正はどのようにして結果から得られるだろうか。
現段階では、速度の時系列をフーリエ変換したグラフの周波数が2ｆ以上の面積を補正と呼ぶことにする。 図８の赤く塗りつぶされている部分が補正である。

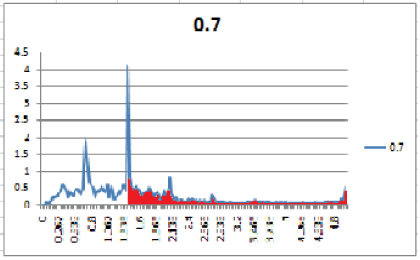
補正の結果としては、ターゲットの周波数が高くなるにつれて補正も大きくなる傾向にあった。

今後の予定

これまで、視覚追従の実験方法と、そこから得られる結果からの言葉の定義、そしてその結果を見てきた。 結果の考察はともかくとして、ここで疑問が二つある。一つ目が、リズムについてだ。 リズムは円運動をすることによってうまれているのではないかと思う。 ただ、単純に円運動をした場合、速度のフーリエ変換ではピークが出るのではないだろうか。 これが第一の疑問である。したがって、まずはただ円運動をした時にどのような結果になるのかを実験したい。
次に、予測による先行についてであるが、予測とは、現在の外界よりも先のことを言っており、 また、それは現存するものの次の状態を知るということを意味する。 では、この視覚追従でターゲットを予測した場合、人間はどのような反応を示すのだろうか。 予測したならば、ターゲットに対して先行するのかもしれない。
ただ円運動する際にリズムがどのようにでるのか、そして予測する視覚追従では先行性が見られるのか。 これらの実験の詳細については後ほど述べる。