２次のルンゲ・クッタ法
導出
微分方程式標準形
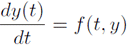(\label{fn})
で表されている場合、ある時刻$t=t_n$における$y$の値を$y(t_n)$とするとき、$y_{n+1}$と$y_{n}$との関係は、次の式で与えられる。
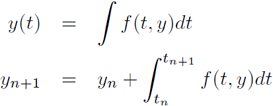(\label{yn})
式(\label{yn})は厳密に成り立っている．$y(t_n)$が既知として、$t_{n+1}$を数値的に見積もる。 $y(t)$を$t_n$の周りで、テーラー展開する。
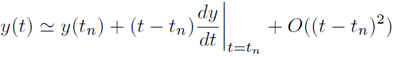
$t=t_{n+1}$とすると次の関係式を得る。
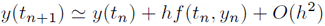(\label{run1})
但し、$h \equiv t_{n+1} - t_n$ で定義される$t$の刻み幅．この関係式は、$y(t_n)$の値が与えられれば、$y(t_{n+1})$が得られることを意味している。 すなわち$y(t_0)$の初期値が与えられれば、任意の時刻の$y(t_n)$が決まる。 但し、1ステップ当たりに$O(h^2)$の誤差が溜まってしまう（図\ref{fig:1-1-1.eps}の左）。
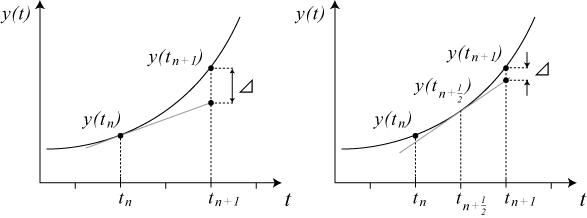
図１
上記のスキームはオイラー法と呼ばれ、$y(t_{n+1})$の値を得るために$y(t_n)$と$\dot{y}(t_n)$を利用した。 より近似精度のよいスキーム考える上で、$t_n$と$t_{n+1}$の中点における$y(t)$の値（$\dot{y}(t_{n+1/2})$）を用いて、$y_{n+1}$を見積もることを考える（図\ref{fig:20081110.eps}の右）。はじめに、$f(t,y)$を$t=t_{n+1/2},y=y_{n+1/2}$の周りでテーラー展開する。
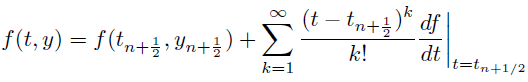(\label{fn2})
式(\ref{fn2})を式(\ref{yn})に代入することで、目標どおり、$y_{n+1}$を$y_n$と$f(t_{n+1/2},y_{n+1/2})$ との関係を導くことができる。
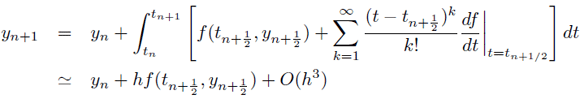
但し、$h=t_{n+1}-t_n$としている。あと、未知な値は$f(t_{n+1/2},y_{n+1/2})$中の$y_{n+1/2}$であるので、 $y_n$の周りで展開する。
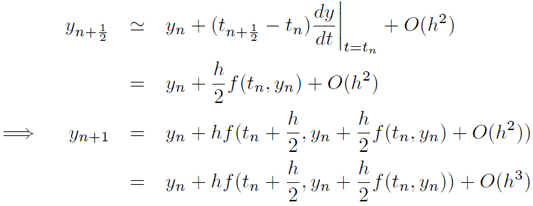(\label{run2})
この結果は２次のルンゲ・クッタ法として知られ、１ステップ当たりの誤差は$O(h^3)$となるり、オイラー法の誤差$O(h^2)$と比較すると精度が上がっていることが分かる。 微分方程式の標準形は一般的に連立方程式で表されベクトル形式
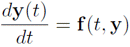
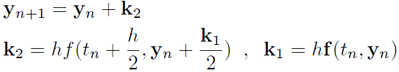
例：１次元調和振動子
２次のルンゲ・クッタ法の計算精度を確かめるために、１次元調和振動子の場合を考える。 調和振動子とは、原点方向へ原点からの距離に比例した力が働き振動す振動子のことで、簡単な例は理想的なばねにつながれた物体を表している。質量$m$、ばね定数$k$の時刻$t$のときの、質点の原点からの変位を$x(t)$とするとき、微分方程式と一般解は次のとおりとなる。
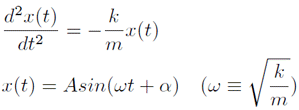
\label{20081114-1}
\label{20081114-2}
但し、$A$と$\alpha$は積分定数で、系の初期状態x(0)とv(0)が与えることで一意に決まる。 また、 $\omega$は角振動数を表している。前節で導いた２次のルンゲ・クッタ法の計算結果と式(\ref{20081114-2})の解析解を比較することで誤差を見積もることができる。
微分方程式を標準形に変換する。
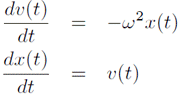
上記２式の連立方程式は式(\ref{20081114-1})と同値であるが、これは単純な数学的トリックだけではなく、古典的ハミルトニアンの正準方程式と同等の意味を持っている。２つの変数$x(t)$と$v(t)$をそれぞれ$y^{(1)}(t)$、$y^{(2)}(t)$とするベクトル形式で表す。
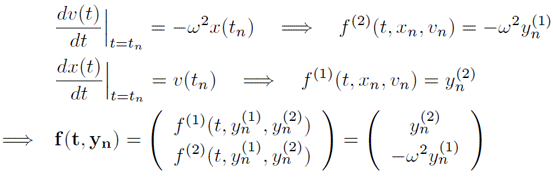
DirectXを用いた描画
運動の様子をDirectXを利用して可視化する。 （Visual C++ 2008 でDirectXを利用する方法はこちらを参照されたし） 角速度$\omega = 1$、初期状態$x(0) = L =200, v(0)=V=0$とし、また時間刻みを$h=0.1$で計算する。
#include "DxLib.h"
// 関数のプロトタイプ宣言
double F1( double t , double y1 , double y2 );
double F2( double t , double y1 , double y2 );
double omega = 1.0 ;
double dt = 0.1 ;
int WINAPI WinMain( HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow ){
ChangeWindowMode(TRUE); //: ウインドウモードで起動（「FALSE」でフルスクリーンモード）
if( DxLib_Init() == -1 ) return -1 ; //ライブラリの初期化（失敗したら終了）
int Cr= GetColor(255,255,255);
int n = 0;
double y[2], k1[2], k2[2];
y[0] = 200.0;
y[1] = 0.0;
while(ProcessMessage()==0 && CheckHitKey(KEY_INPUT_ESCAPE)==0){
ClsDrawScreen();
n++;
k1[0] = dt * F1( double(n) , y[0] , y[1]);
k1[1] = dt * F2( double(n) , y[0] , y[1]);
k2[0] = dt * F1( double(n) + 0.50 * dt , y[0] + k1[0]/2.0 , y[1] + k1[1]/2.0 );
k2[1] = dt * F2( double(n) + 0.50 * dt , y[0] + k1[0]/2.0 , y[1] + k1[1]/2.0 );
y[0] = y[0] + k2[0];
y[1] = y[1] + k2[1];
DrawCircle( int(y[0]) + 300 , 200 , 20 , Cr ,TRUE) ;
//備考：画面サイズはデフォルトで、640×480
// printfDx("(%d,%d)\n",x,v);
ScreenFlip();
}
WaitKey() ;
DxLib_End() ; // ＤＸライブラリ使用の終了処理
return 0 ; // ソフトの終了
}
double F1( double t , double y1 , double y2 ){
return y2;
}
double F2( double t , double y1 , double y2 ){
return -1.0 * omega * omega * y1;
}
図２：実行画面
上記サンプルソースでは、「1秒間に計算する回数」＝「1秒間に画面に描画する回数（リフレッシュレート）」となっている。
誤差の見積もり
次に、２次のルンゲ・クッタ法での数値計算結果と、式(\ref{20081114-2})で得られた解析解とを比較する。 $t=t_n$（$t_n=hn$）のときの解析解を$x(t_n)$、計算結果を$x_n$と表したとき、誤差を次の式で評価する。
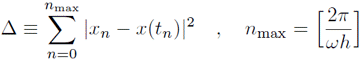
上式は、質点が１周期のする間の解析解との誤差の２乗の和を表している（但し、$[\cdots]$はガウス記号）。$h$の値を小さくすることで計算誤差が小さくなることを確かめてみる。
#include <math.h>
#include <fstream>
#include <iostream>
using namespace std;
// 関数のプロトタイプ宣言
double x( int n );
double F1( double t , double y1 , double y2 );
double F2( double t , double y1 , double y2 );
double PI = 3.14159265358979323846;
double omega = 1.0 ;
double L = 200.0;
double V =0.0 ;
double h;
//ファイル出力
ofstream ofs1( "result1.data" );
int main()
{
double y[2], k1[2], k2[2];
double delta;
for(int j=1 ; j<=14 ;j++ ){
delta = 0.0;
y[0] = L;
y[1] = V;
h = 1.0/pow( 10.0 , double(j)/2.0 );
int max_n = int(2.0* PI /(h * omega ));
for(int n=0 ; n<= max_n ; n++){
delta += (y[0] - x(n)) * (y[0] - x(n));
k1[0] = h * F1( double(n) , y[0] , y[1]);
k1[1] = h * F2( double(n) , y[0] , y[1]);
k2[0] = h * F1( double(n) + 0.50 * h , y[0] + k1[0]/2.0 , y[1] + k1[1]/2.0 );
k2[1] = h * F2( double(n) + 0.50 * h , y[0] + k1[0]/2.0 , y[1] + k1[1]/2.0 );
y[0] = y[0] + k2[0];
y[1] = y[1] + k2[1];
}
ofs1.precision(30);
ofs1 << j << " " << delta << endl;
cout << j << endl;
}
}
double x(int n){
return L0 * cos( h * n);
}
double F1( double t , double y1 , double y2 ){
return y2;
}
double F2( double t , double y1 , double y2 ){
return -1.0 * omega * omega * y1;
}
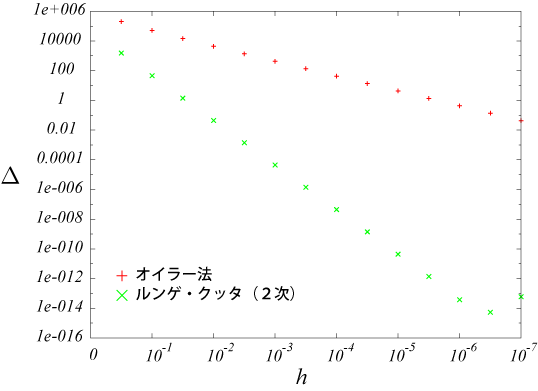
図３：計算結果
図(３)は、オイラー法と２次のルンゲ・クッタ法における計算結果での誤差と、時間刻み$h$の関係を表している。$h$を小さいほど誤差も小さくなる。１ステップごとの誤差はそれぞれ式(\ref{run1})式(\ref{run2})で与えられたとおり、$O(h^2)$と$O(h^3)$であるので、$h\sim 10^{-6}$の場合には、１ステップあたりの誤差は、２次のルンゲ・クッタの場合$\Delta \sim 10^{-18}$程度となる。本計算機環境での倍精度（double型）における有効桁数は１６桁であるため、$h\sim 10^{-6}$より小さくする必要がない。$h\sim 10^{-7}$の場合にむしろ誤差が増加している。
次回
４次のルンゲ・クッタ法の導出を行う。
