今週の授業では衝突係数を(12/05)

今週の授業にて

今週の授業では、少年に衝突係数を説明した。そのことについて。
さて、衝突係数とは何か。まず、ボールを地面に落とした時を考えてみる （ちなみに、今回、重力はなどは考えない）。 これを示したのが図1だ。

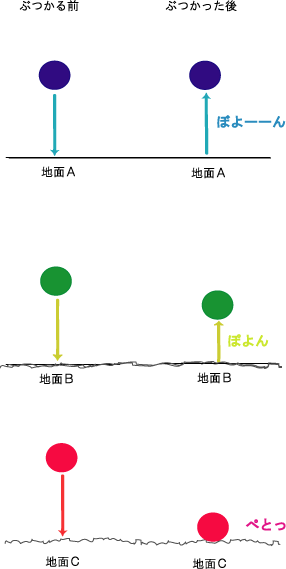
図１

それぞれの地面でぶつかる前とぶつかった後では、なにが変わっているのだろうか。ここで変化しているのは速度である。
ちなみに、速度とは、ある軸の＋、－のどちらの方向にどれくらいの速さがあるのかを示すものである。例えば地面Ａの場合、 地面にy軸の０をとり、ボールのｙ座標が５、つまり、ボールの衝突前・後の速さがどちらも5であったとする。
すると、それぞれの速度は、ぶつかる前は速度が-5、ぶつかった後は速度は5となる。 図2を見ると、速さ５で移動すると、その結果0の地点にいても、10の地点にいても、どちらも良い。
では、「速度５で移動してください」という指示であったらどうだろうか。 その場合、図2の左下の図とおなじ、10の地点にいるはずで、「速度－５で移動してください」という指示であれば、 図2の右下の図と同じ、0の地点にいるはずだ。

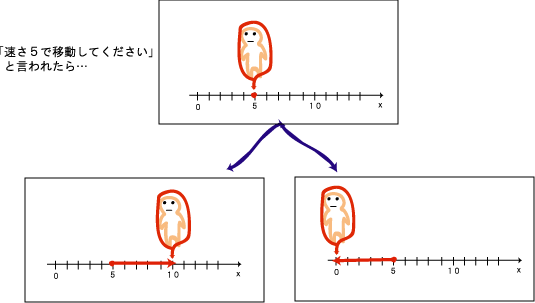
図２

さて、ボールが跳ね返るのだからボールの運動方向(＋、－)が変わるのは当たり前だが、速さが変わるのはなぜだろうか。それは、地面の固さ、柔らかさのせいである。固い地面にボールを落とすのと、スポンジのような柔らかい地面にボールを落とすのとでは跳ね返る前と跳ね返った後の速さが違うのは直感的に分かるだろう。
衝突係数とは、大きく言えば、この地面の性質を表すようなものである。
ちなみに、衝突係数は「e」と表記されるらしい。式としては、e=-V2/V1 で表され、V1はぶつかる前の速度、V2はぶつかった後の速度である。なぜマイナスが付いているかというと、 ぶつかった後（V2）とぶつかる前（V1）は、当然進む方向が違うので、符号はどちらかが＋で、どちらかが－になる。
これを割り算すると 、答えには当然マイナスがつく。式についているマイナスは、これを消すためのものである。たぶん。
極端な例を考えると、図1の地面Ａのように同じ速度で跳ね返るか、図1の地面Ｃのように跳ね返らないか、ということになる。 つまり、衝突係数eは、0≦e≦1 となり、ぶつかる相手（または自分）が柔らかいほど、0に近づき、固いほど1に近づく。たぶん。