コッホ曲線を描く

コッホ曲線とは

コッホ曲線（von Koch curve）とは、それぞれの線分を３等分し、等分した２点を頂点とする正三角形を作図することを無限に繰り返すことで得られる図のことである。 コンピュータ上では、無限回繰り返すことは不可能なので、有限回繰り返した図を作図した結果は次のとおり。

コッホ曲線

n世代目のコッホ曲線を描く

コッホ曲線の任意の線分の$n-1$世代目と$n$世代目のと関係式を導くことによって、任意の世代におけるコッホ曲線を漸化式で得る（図\ref{fig:koho-1}）。

n世代のコッホ曲線

$n$世代の$m$番目の頂点の位置ベクトルを$x^{(n)}_m$とする場合、$n-1$世代と$n$世代の関係式は次の通りとなる。

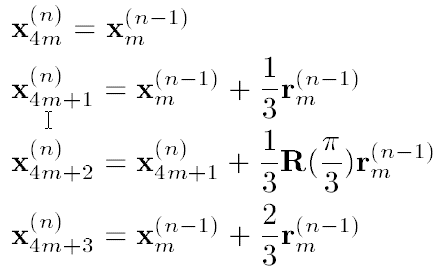
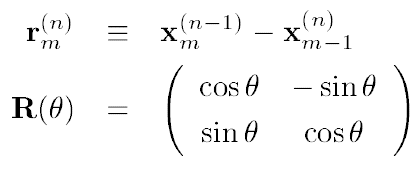
${\bf r}^{n}_m$は$n$世代目における、左から$m$番目の線分のベクトルを表し、$R(\theta)$は回転行列である。 また、0世代目の線分の長さを$L$としたときの初期値は、線分の両端の位置ベクトル$x^{0}_0 =(0 \ 0)^{T}$、$x^{0}_1 =(L \ 0)^{T}$であたえられる（$T$は転置行列の意）。

#include <math.h>
#include <fstream>
#include <iostream>
#include <string> 
using namespace std;

//ファイル出力
//ofstream ofs1( "kohho1.data" );
int main()
{
	double PI = 3.14159265358979323846;

	double x[7][4100][2];
	x[0][0][0] = 0.0;
	x[0][0][1] = 0.0;
	x[0][1][0] = 100.0;
	x[0][1][1] = 0.0;
	int max_n = 6 ;
	for(int n =1 ; n<=max_n ; n++){
		for(int m = 0; m < int(pow(4.0, n))/4 ; m++){
			x[n][4*m][0] = x[n-1][m][0];
			x[n][4*m][1] = x[n-1][m][1];
			x[n][4*m+1][0] = x[n-1][m][0] + 1.0/3.0 * (x[n-1][m+1][0] - x[n-1][m][0]) ;
			x[n][4*m+1][1] = x[n-1][m][1] + 1.0/3.0 * (x[n-1][m+1][1] - x[n-1][m][1]) ;
			x[n][4*m+2][0] = x[n][4*m+1][0] + 1.0/3.0 * ( cos(PI/3.0) * (x[n-1][m+1][0] - x[n-1][m][0]) - sin(PI/3.0) * (x[n-1][m+1][1] - x[n-1][m][1]) ) ;
			x[n][4*m+2][1] = x[n][4*m+1][1] + 1.0/3.0 * ( sin(PI/3.0) * (x[n-1][m+1][0] - x[n-1][m][0]) + cos(PI/3.0) * (x[n-1][m+1][1] - x[n-1][m][1]) ) ;
			x[n][4*m+3][0] = x[n-1][m][0] + 2.0/3.0 * (x[n-1][m+1][0] - x[n-1][m][0]) ;
			x[n][4*m+3][1] = x[n-1][m][1] + 2.0/3.0 * (x[n-1][m+1][1] - x[n-1][m][1]) ;
			x[n][4*m+4][0] = x[n-1][m+1][0];
			x[n][4*m+4][1] = x[n-1][m+1][1];
		}
		x[n][int(pow(4.0, n))][0] = x[n-1][int(pow(4.0, n-1))][0];
		x[n][int(pow(4.0, n))][1] = x[n-1][int(pow(4.0, n-1))][1];

		char sh[10];
		string kk,kk0 = "";
		sprintf(sh, "%d", n);
		kk = kk0 + "Koch" + sh + ".data";
		ofstream ofs1( kk.c_str() );
		for(int i=0; i<= int(pow(4.0, n));i++ ){
			ofs1.precision(5);
			ofs1 << x[n][i][0]  << " " << x[n][i][1] << endl;
		}
		cout << n << endl;
	}
}

今後の予定

フラクタル次元についてまとめる