multifractal（マルチフラクタル）概説

multifractal 構造

multifractal 構造をもつ集合の代表として，図\ref{Cantor}のようなCantor setを考える．

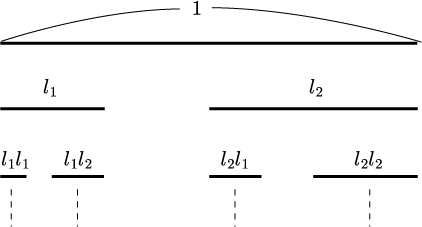
Cantor set（\label{Cantor}）

この集合は$l_1 + l_2 < 1$としたとき，$1$の長さの線分からそれに含まれる部分をくり抜いて，$l_1とl_2$の部分だけを残す場合を考える． これを$n$回繰り返して得られる集合を，第$n$世代の Cantor set と呼ぶことにする． この集合は場所によって線分の長さが違っている． さらに第n世代の Cantor set 各区間 $I_i$（$i = 1,2,\cdots N_n, \; N_n = 2^n$）に適当な規則により確率$p_i$付与する． 定義により，$\sum_ip_i = 1$となる． 極限として得られるこのような集合を特徴付けるために，局所次元 $\alpha$ と $f(\alpha)$という量を導入する． この解析方法は，1987年にT. C. Halseyらによって考案され[1]，{\bf $f(\alpha)$--spectrum}の方法として知られている． さらにM. Kohmotoによって，上記の量を熱力学関数と対応をつけて定式化された[2]．

ここでは，集合全体の特徴を定量的に表す{\bf 一般化次元$D_q$}と， 局所的な集合の特徴を表す{\bf 局所次元(singularity) $\alpha$}が$f(\alpha)$という量で関係付けられることを簡単に示す．

始めに，$l_1 = l_2 = \cdots = l_{N_n}\equiv l^{(n)}$である場合の一般化次元$D_q$を次のように定義する：

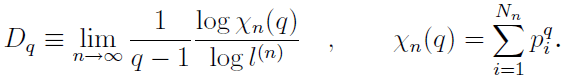
\label{C.19}

$D_q$は$q$の値によって，いろいろな種類の次元を包括している：

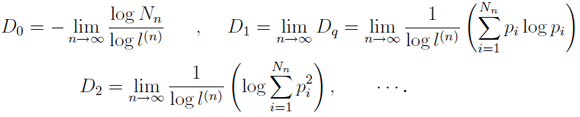
容量次元$D_0$，情報次元$D_1$，相関次元$D_2$，$\cdots$と，$D_q$はよく知られた次元を$q$という量で統一的に表すことができる．

しかし(\ref{C.19})式では図\ref{Cantor}のような線分の長さが場所によって異なった集合には，このままでは適用ができない． そこでこれを拡張するために次の量を導入する：

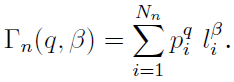
\label{C.20}

$q$を決めて両辺$n\to \infty$の極限をとったときに，右辺は $\beta$ がある値以下ではゼロに収束するが，その値を超えると発散する． その境界における $\beta$ の値を$\beta(q)$ と記し，拡張一般化次元$\tilde{D}_q$ を関係式 $\beta(q) = (1 - q)\tilde{D}_q$ により定義する． 一般に$\tilde{D}_q < D_q$を満たしている．
また，幾何学的な構造のみに着目する場合には$p_i = 1/N_n$（一定）とすればよい． 詳しい計算は参考文献\cite{6},\cite{7}にあるので，本稿では結果だけを記すことにする．

局所次元 $\alpha$ という量を確率測度$p_i$に対して定義する：

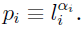
また，multifractal 解析でもっとも大事な関数に$f(\alpha)$という関数がある． この量はある集合のうち局所次元が $\alpha$ である部分集合の容量次元を表している． $\alpha$ と$q$の関係は

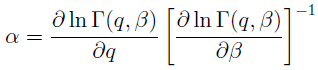
で与えられる．ただし，右辺を計算した後で，$\beta = \beta(q)$ とおくものとする． さらに，$f(\alpha)$は拡張一般化次元$\tilde{D}_q$とは次の関係式により結ばれる：

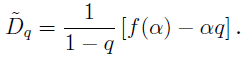
$\alpha$ と $f(\alpha)$は$q$の関数として，自己相似構造をもつ集合（１次元）の各線分$l_i \ (i = 1,2,\cdots)$が与えられたときに， $q$の値に対してそれぞれ定量的に求められる． 逆に，$\alpha$ と $f(\alpha)$に対して，対応する$\tilde{D}_q$が決まる． 図\ref{Cantor}の Cantor set で，$l_1 = \frac{1}{4}, l_2 = \frac{1}{2}$として計算した結果が図\ref{Cantor1}である．

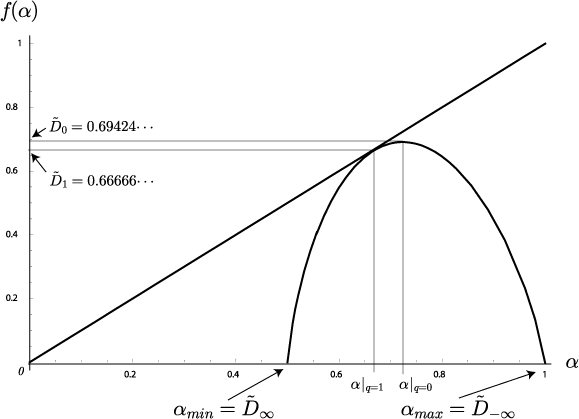
Cantor setの $f(\alpha)$--spectrum}（\label{Cantor1}）

$f(\alpha)$は$q = 0$で最大値$f(\alpha) = \tilde{D}_0$をとり，$q\to \infty$のときに $\alpha_{\rm min}$で$f(\alpha) = 0$， $q\to -\infty $のときに $\alpha_{\rm max}$で$f(\alpha) = 0$である上に凸の関数となる． 図\ref{Cantor}の Cantor set では，局所的に連続的である（$\alpha = 1$）部分から $\alpha = 0.5$で表される部分まで， 図\ref{Cantor1}のように分布していることを表している．

[1] T. C. Halsey, M. H. Jensen, L. P. Kadanoff, I. Procaccia and B. I. Shraiman Phys. Rev. A 33, (1986) 1141
[2] M. Kohmoto Phys. Rev. A 37, (1988) 1345

今後の予定

■ multifractal の導出
■ 様々な集合のmultifractalの解析を行なう