授業実施報告(11月~1月)
11月21日
応用講座では各自が研究テーマをもち、シミュレーションの構築を行っている。ここ数回の応用講座では、シュミレーション構築で共通する概念として、運動量の保存則にもとづいた物体の衝突をシミュレーションしている。
授業内容
物体に力を加えるときに起こる速度の変化を考える。物体の運動量の変化は、物体に加えられた力積によって与えられる。運動量とは、物体の質量と速度の積である。
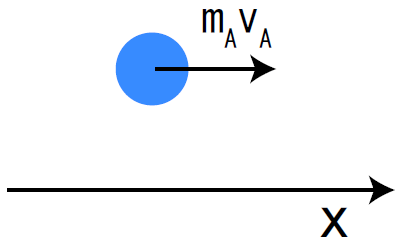
Figure : Momentum of Object A
力積とは、物体に加えられた力と、力が加えられた時間の積である。加えられた力積と運動量の変化は以下の式によって与えられる。
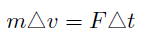
ここで、時間軸t、空間軸x、速度の軸v を導入し、物体の運動量の変化を明示的に記述すると、
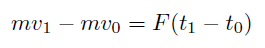
さて、ここで物体A と物体B の二つの物体の衝突を考える。衝突の際には、作用反作用の法則により、ふたつの物体が受ける力は等しい。
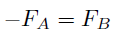
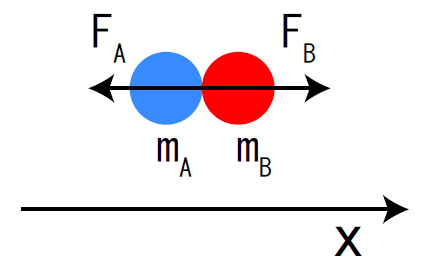
Figure : Collistion of Object A and B
ここで、FA とFB は力の大きさを表す。作用・反作用の法則において、力の向きは常に逆向きになるので、これをマイナスの符号で表す。物体A は衝突によって、物体B から力積を受け、運動量が変化する。このことを式で表すと、
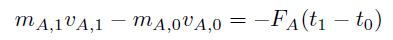
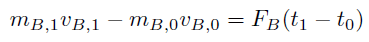
二つの式を足すと、作用・反作用の法則より、右辺がキャンセルするので、以下の式が得られる。
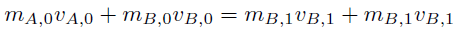
左辺は衝突前における物体A と物体B を足した運動量であり、右辺は衝突後の物体A と物体B を足した運動量になっている。つまり、衝突前と衝突後の運動量の和が保存しているという式が導かれた。次に衝突係数の計算である。
物体A が床に衝突した場合は、以下の式のように衝突係数が計算される。
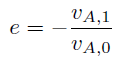
v_{A,1} はもちろん、速度である。衝突前後の速さが等しければ、衝突係数は1である。このときの衝突を完全弾性衝突といういう。衝突後に速さが0になれば、衝突係数は0である。このときの衝突を完全非弾性衝突といういう。物体A と床の材質によって、衝突係数は決まる。二つの物体が衝突する場合は、物体A からみた相対速度を考え、
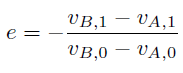
衝突前の物体の速度は既知なので、衝突後の二つの物体の速度を知りたいが、二つの未知な変数に対して、方程式が二つ存在するので、解くことができて、物体A の衝突後の速度は、
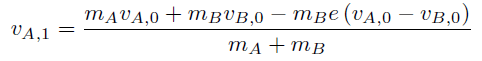
物体B の衝突後の速度は、
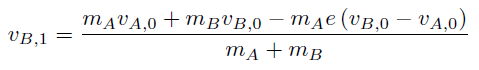
この数式を用いて、衝突する前の物体の速度から、衝突後の物体の速度を導くことができ、衝突のシミュレーションを行うことができる。今回は一直線上での衝突を考えたが、xy 平面における衝突も同様に考え、x 方向に対する運動量の保存則とy方向に対する運動量の保存則を立てて、計算を行う。
当日の様子
vA と書いた時に、この記号が物体A の速度をあらわすか、物体B の速さを表すかが、ポイントである。つまり、vA と変数を宣言したときに、単に数字ではなく、なんの物理量を表したいかである。衝突前の二つの物体の速度は知っているとしよう。いま、知りたいことは衝突後の物体の速度であるが、衝突後に速さがどの向きかは、あらかじめ知ることができない。したがって、vA は物体A の速度を表していると考えるのが便利である。速さの向きは計算が終わったあとに、自動的にでてくる。このvA という変数で何を表したいのかが、ひとつ目のポイントであった。速さが速度かで議論をした。次に衝突係数の計算において、ボールが床に衝突するときは、みんな問題なく考えられたが、二つの物体の衝突のときに相対速度を考えるところで議論した。車に乗っている時に、自分の車の速度によって、他の車の速度が違ってみえるのは、二つの車の相対速度を認識しているからである。

12月5日
応用講座では、大きく分けて、決定論と確率論によるシミュレーションの構築を行っている。決定論の方では、分子の運動論から、熱力学における法則をシミュレーションする。確率論の方では、まずランダムウォーク、ガウス分布をシミュレーションし、ランジュバン方程式などの微分方程式の数値計算も行う。
授業内容
気体の分子運動の第一歩として、2 個の物体が衝突するときのシミュレーションを行っている。物体の水平方向と鉛直方向の運動量の保存則の数式をたてて、計算する。応用講座のレベルのシミュレーションでは、まず現象をよく観察し、数式を使って定式化するところから始める。生物の行動のアルゴリズムとして、基本的な要素のひとつであるランダムウォークの構築を行っている。まずはランダムウォークから、駆動粒子の分布を導き出すことをやっている。
※【参考】今週の授業では衝突係数を(12/5)
当日の様子
基礎講座もここまでくれば、等速運動と等加速度運動をxy 平面で考えることができるようになり、直感的にシミュレーションを構築することができる。そこで、より大事になるのは、「なぜ、シミュレーションできたか?」を立ち止まって、考えることである。速度のベクトル合成を考え、ボールの位置が速度によってどのように合成されるかを考察としてまとめた。放物運動まですんなり来たので、次に地面との衝突にを考えにいれたシミュレーションもおこなった。衝突前後のボールの鉛直方向の速度変化を衝突係数を使ってあらわし、シミュレーションすることができた。

12月12日
授業内容
気体の分子運動の第一歩として、2 個の物体が衝突するときのシミュレーションを行っている。二つの物体が衝突する際に、どの方向にボールが反射するかの因果関係をつかんでシミュレーションを構築する。x 方向とy方向、それぞれの座標軸に対して、運動方程式をたてて、運動量保存の式を導く。
12月26日
授業内容
今日はプログラムの開発環境として、Borland 社のC コンパイラの使い方と、OpenGL を使った描画の基本的なプログラムの構築を行った。
当日の様子
できるだけシンプルなプログラム構成と描画のプログラムを考えた場合、OpenGL を使ったプログラム開発は、データファイルへの出力やコマンドプロンプトへの書き出しなどの扱いもしやすい。応用講座においては、この開発環境を以後、使っていく予定である。
1月9日
授業内容
データ解析の手法としてフーリエ解析の説明を行った。実験データを読み込み、フーリエ解析を行うわけだが、時系列で記述されたデータをフーリエ変換する際に、元データのx 軸の値から、フーリエ変換後の周波数のx 軸をつくる方法を説明した。例えば、元のデータで一秒間の60 回のサンプリングが行われているとすると、0 から1 の間で、1波長をもつsin 関数を用意する。データ点の間隔は元データと同じように60点とする。このsin 関数をフーリエ変換して、ピークが出てくるが、ピークの位置が丁度、1になるように新たなx 軸を用意すればよい。つまり、1秒の周期に対して、1Hz を対応されることと、離散フーリエ変換なので、サンプルレートに注意して、新たなx 軸の設定を行う。フーリエ変換の理論に入る前に、周期と周波数の単純な関係を理解することが必要だった。全体としては、OpenGL を使ったプログラムが実装された。プロンプトとファイルへの書き出しや、描画環境としてもシンプルで使いやすい。
1月16日
授業内容
斜めに立てかけてある壁に、ボールを衝突させたら、どのように跳ね返るだろうか?
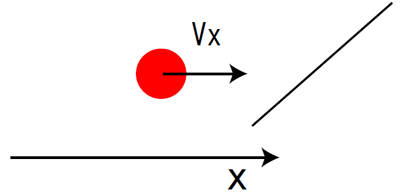
Figure : 斜面への物体の衝突
衝突後のボールの速度を求めるいくつかの方法があるだろうが、斜面の角度に従って、回転行列を使う方法が汎用性が高い。授業ではまず回転行列の求め方として、座標を回転したときに、どのようにある点Aの座標(x,y)が変換されるかを求める計算の仕方を教えた。























