モンテカルロ法を試す―円周率の評価―

確率法則を用いて問題を解くモンテカルロ法（Monte Carlo meyhod）では、質のよい乱数が必要である。 C言語で用意されている関数randと、高品質で高速に乱数を生成できるとして知られるメルセンヌ・ツイスタを利用して、円周率を評価してみる。 また、その際のアルゴリズムとして「あたりはずれ法」と「粗いモンテカルロ法」を用いて計算する。

円周率の評価

図１のような単位円の第１象限領域の面積をモンテカルロ法にて求め、 解析的に求められる面積$\pi/4$と比較することによって、円周率の評価を行うことにする。

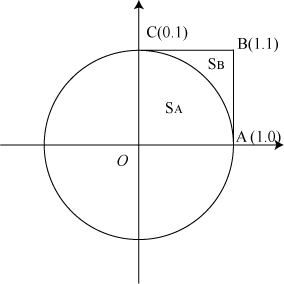
図１．単位円の第１象限領域

あたりはずれ法

あたりはずれ法とは、面積を評価したい領域$S_A$を面積が既知の領域$S$で囲み、 領域$S$上に分布が一様になるように$N$個の点を降らせる。 領域$S_A$上に落ちた点の数が$N_A$であれば、$S_A$の面積は、

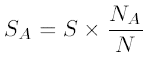
で評価することができる。
図１の第１象限領域$S_A$の面積は、既知の領域$S$を正方形OABCとすると面積が1なので都合よく$N_A/N$で求まる。
つまり、区間$[0,1]$の一様乱数のペア$(\xi,\eta)$を$N$個用意したとき、$S_A$の内部、つまり$\xi^2+\eta^2<1$を満たす個数を$N_A$とすることで、 $\pi/4=N_A/N$より$\pi$を評価することができる。

粗いモンテカルロ法

粗いモンテカルロ法は、平均値の定理

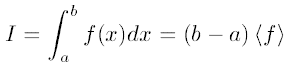
を利用する。これは「$f$の区間$[a,b]$の積分値は、$f$の区間$[a,b]$の平均値$\left\langle f \right\rangle$に幅$b-a$を掛けたものに等しい」ことを意味している。 $\left\langle f \right\rangle$を、区間$[a,b]$上に分布が一様になるように$N$個の点を降らせ、その平均を取ることで評価する。

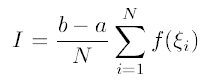
但し、$\xi$は乱数。
図１の場合、

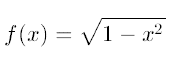
区間は$[0,1]$である。乱数の組$\{x_i\} (i=1,2,\cdots ,N)$から$\left\langle f \right\rangle$を見積もり、面積$S_A$を求め、 $\pi/4=S_A$より$\pi$を評価することができる。

Visual C++ 2008で数値計算

円周率を２つのアルゴリズム「あたりはずれ法」と「粗いモンテカルロ法」の場合において、
２つの擬似乱数生成器、「C言語の関数rand」と「メルセンヌ・ツイスタ（MT）」を利用して、それぞれの計算結果を比較してみる。

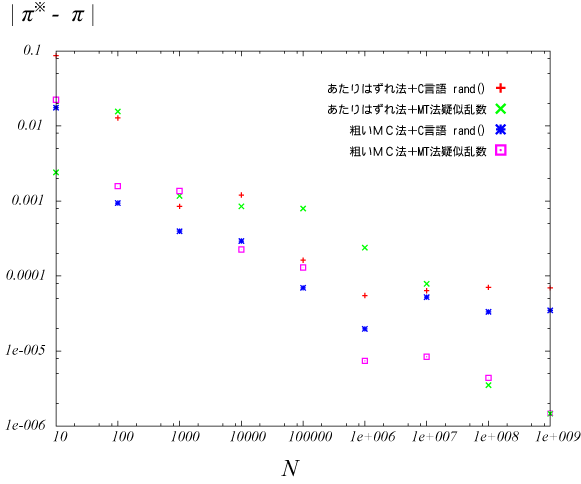
図２．計算結果

図２は、$N$の値を$10^1～10^9$まで、それぞれの$N$に対して１００回計算しその平均から見積もった円周率$\pi^{*}$と、 有効桁数９の円周率の真の値$\pi$（=3.14159265）とのずれをプロットした。 図２の結果から、C言語のrandを利用した場合、Nが$10^7$より大きな値でも精度が上がっていないことが分かる。 これは、C言語のrandで生成される乱数の列に何らかの偏りがあるためであろう。

今回は、「あたりはずれ法」とそれよりも計算精度の良い「粗いモンテカルロ法」の計算結果を比較すると、 $N$の小さなところでは後者のほうが一桁精度がよいが、$N$の大きなところでは、ほとんど差がない結果となった。

プログラム

今回の数値計算で使用したメルセンヌ・ツイスタは、
http://www.math.sci.hiroshima-u.ac.jp/~m-mat/MT/MT2002/mt19937ar.html
にある「mt19937ar.c」のメイン関数を削除したファイルを「mt19937ar.h」とし、利用させていただいた。

あたりはずれ法による円周率の計算

/*
当たり外れ法による円周率の計算
*/
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <iostream>
#include <string> 
#include "mt19937ar.h"  //メルセンヌ・ツイスタ
using namespace std;

double PI = 3.14159265358979323846;

// 関数のプロトタイプ宣言
double f( double x);
//ファイル出力
ofstream ofs1( "a_MT.data" );   //メルセンヌ・ツイスタ利用の場合
ofstream ofs2( "a_rand.data" ); //c言語rand利用の場合

int main(){
	srand((unsigned)time(NULL));
	init_genrand((unsigned)time(NULL));

	int N_max = 1000000000;
	int ave = 100;
	int N_A = 0;
	int N_A2 = 0;
	int step = 1;
	double N_sum[10] = {0.0};
	double N_sum2[10] = {0.0};

	for(int j=1; j<=ave; j++){
		step = 1;
		N_A = 0;
		N_A2 = 0;
		for(int i=1; i<=N_max; i++){
			double zi = genrand_real1();
			double eta = genrand_real1();
			if(f(zi) > eta ) N_A++;

			zi = (double)rand()/(double)RAND_MAX;
			eta = (double)rand()/(double)RAND_MAX;
			if(f(zi) > eta ) N_A2++;

			if(i==10 || i==100 || i==1000 || i==10000 || i==100000 || i==1000000 || i==10000000 || i==100000000 || i==1000000000){
				N_sum[step] += double(N_A)/double(i) *4.0;
				N_sum2[step] += double(N_A2)/double(i) *4.0;
				step++;
			}
		}
		cout << j <<endl;
	}

	for(int j=1; j<=9; j++){
		ofs1 << pow(10.0,j) << " " << N_sum[j]/double(ave) << " " << fabs( N_sum[j]/double(ave) - PI) << endl;
		ofs2 << pow(10.0,j) << " " << N_sum2[j]/double(ave) << " " <<  fabs( N_sum2[j]/double(ave) - PI) << endl;
	}


}
double f(double x){
	return  sqrt( 1.0 - pow(x ,2));
}

粗いモンテカルロ法による円周率の計算

/*
粗いモンテカルロ法を用いた求積
*/
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <iostream>
#include <string> 
#include "mt19937ar.h"
using namespace std;

double PI = 3.14159265358979323846;

// 関数のプロトタイプ宣言
double f( double x);
//ファイル出力
ofstream ofs1( "result.data" );
ofstream ofs2( "result2.data" );

int main(){
	srand((unsigned)time(NULL));
	init_genrand((unsigned)time(NULL));

	int N_max = 1000000000;
	int ave = 100;
	int N_A = 0;
	int N_A2 = 0;
	int step = 1;
	double N_sum[10] = {0.0};
	double N_sum2[10] = {0.0};
	double F_sum = 0.0;
	double F_sum2 = 0.0;

	for(int j=1; j<=ave; j++){
		step = 1;
		N_A = 0;
		N_A2 = 0;
		F_sum = 0.0;
		F_sum2 = 0.0;

		for(int i=1; i<=N_max; i++){
			F_sum += f(genrand_real1());
			F_sum2 += f((double)rand()/(double)RAND_MAX);

			if(i==10 || i==100 || i==1000 || i==10000 || i==100000 || i==1000000 || i==10000000 || i==100000000 || i==1000000000){
				N_sum[step] += F_sum/double(i) *4.0;
				N_sum2[step] += F_sum2/double(i) *4.0;
				step++;
			}
		}
		cout << j <<endl;
	}

	for(int j=1; j<=9; j++){
		ofs1 << pow(10.0,j) << " " << N_sum[j]/double(ave) << " " << fabs( N_sum[j]/double(ave) - PI) << endl;
		ofs2 << pow(10.0,j) << " " << N_sum2[j]/double(ave) << " " <<  fabs( N_sum2[j]/double(ave) - PI) << endl;
	}


}
double f(double x){
	return  sqrt( 1.0 - pow(x ,2));
}

今後の予定

モンテカルロ法を用いて、熱力学量を計算してみる