カントール集合のマルチフラクタル(multi-fractal)解析

l_1 = 1/4 , l_2 = 1/2 のカントール集合についてのマルチフラクタル(multi-fractal)解析を行う。
（※マルチフラクタル(multi-fractal)解析についてはこちらをご覧ください）

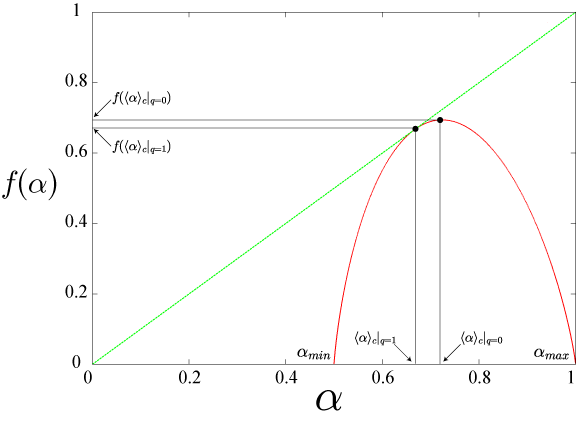
マルチフラクタル(multi-fractal)解析

厳密解

■ハウスドルフ(Hausdorff)次元：D_H = f(<\alpha>_c|_{q=0}) = log(1+\sqrt(5))/log2 = 0.69424・・・
■局所次元 <\alpha>_c|_{q=0} = 2/(5-\sqrt(5)) = 0.723606・・・
※１．集合全体のハウスドルフ次元は、局所次元 \alpha = <\alpha>_c|_{q=0}）となる部分集合の容量次元と一致する。
※２．ハウスドルフ次元（D_H）と一般化容量次元（\tilde D_0)は一致する。

■一般化情報次元 \tilde D_0 = <\alpha>_c|_{q=1} = f(<\alpha>_c|_{q=1}) = 2/3 = 0.66666・・・
※局所次元 \alpha = <\alpha>_c|_{q=1}）と、 局所次元 \alpha = <\alpha>_c|_{q=1}）となる部分集合の容量次元（f(<\alpha>_c|_{q=1})）が一致し、かつ、一般化情報次元と一致する。

■局所次元の最小値：\alpha_{min} = <\alpha>_c|_{q->\infty} = 1/2=0.5
■局所次元の最大値：\alpha_{max} = <\alpha>_c|_{q->-\infty} = 1

VisualC++ ソース

(世代)n=10 のカントール集合における、マルチフラクタル解析のソース。

/*
カントール集合のmaruti-fractal解析
*/
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <iostream>
#include <string>

#include <cstdio>
#include <iomanip>
#include <stdio.h>

using namespace std;

double PI = 3.1415926535897932384;
double e  = 2.7182818284590452354;

//関数のプロトタイプ宣言
int factorial( int n );

ofstream ofs1( "result1.data" );

int main(){
	int N , n=10, a=2, r;
	double R[1024] = {0.0};
	double l_1 = 1.0/4.0 , l_2 = 1.0/2.0;
	double Z,F,Q;
	double alpha_c, beta_c, epsilon_c,f_alpha,q;

	
	N = int(pow(double(a),n));
	r=0;
	for(int j=0; j<=n; j++){
		int g = factorial(n)/(factorial(n-j)*factorial(j));
		for(int k=1; k<=g ;k++){
			R[r] = pow(l_1,j) * pow(l_2,n-j);
			r++;
		}
	}

	for(int i=0; i<2000;i++){
		Z=0;
		beta_c = double(i)/50.0-20.0;
		for(int j=1;j<=N;j++){
			Z+= pow(R[j-1],beta_c);
		}
		F= log(Z)/double(n);
		double sum=0.0;
		for(int j=1;j<=N;j++){
			sum+= log(R[j-1])*pow(R[j-1],beta_c);
		}
		epsilon_c = -1.0/double(n)*sum/Z;
		alpha_c = log(double(a))/epsilon_c;
		Q = F + epsilon_c* beta_c;
		f_alpha = Q/epsilon_c;

		cout << i << endl;
		ofs1.precision(30);
		ofs1 << alpha_c  << " " << f_alpha << endl;

	}
}
int factorial( int n ){
	if ( n > 1 ){
		return n * factorial ( n-1 );
	}else if ( n == 1 || n == 0){
		return 1;
	}
}

次回の予定

マルチフラクタル解析の詳細をまとめる。