レナード・ジョーンズ（ＬＪ）ポテンシャルにおける動径分布（３次元）

モンテカルロシミュレーション（メトロポリスの方法）で、レナード・ジョーンズ（ＬＪ）ポテンシャルにおけるカノニカル集合の動径分布について計算した結果を掲載する。
１．粒子密度（体積）一定で、無次元温度を変化させたときの動径分布を表示
２．無次元温度一定で、粒子密度（体積）を変化させたときの動径分布を表示

※モンテカルロシミュレーション（メトロポリスの方法）の詳細についてはこちらをご覧ください。

注意1:周期的境界条件を課した場合、有効な動径分布の範囲は、0<r^*<L/2 となる。

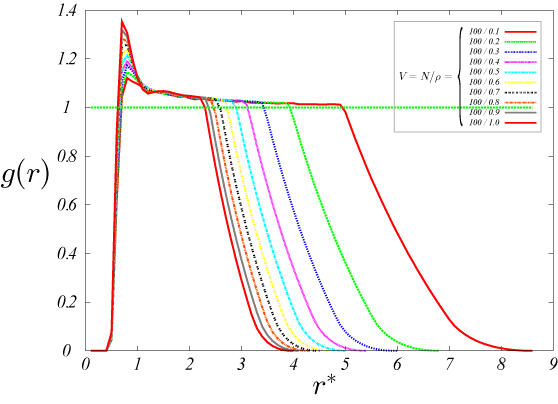
粒子密度（体積）一定の場合

以下の結果から、密度に関わらず、温度が低い時に動径分布 g(r)のr=1.3 付近に鋭いピークがたち、密度が低いほど高い。 1つ目のピークは、ある粒子からみて一つ目粒子の分布を表している。
また、r=2 付近のピークは、2つ目の粒子の分布を表している。

図１．\rho=0.1

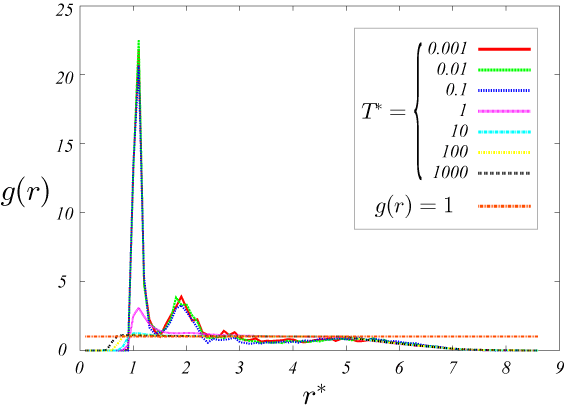
図２．\rho=0.2

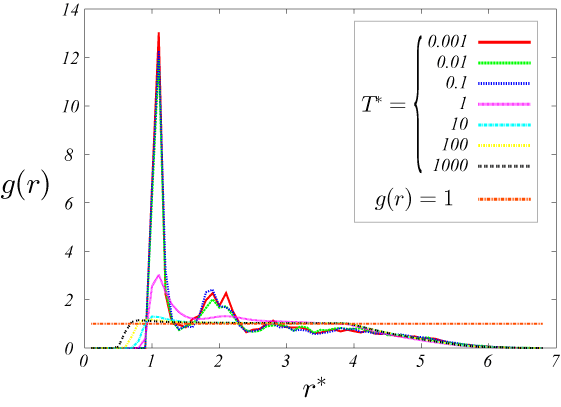
図３．\rho=0.3

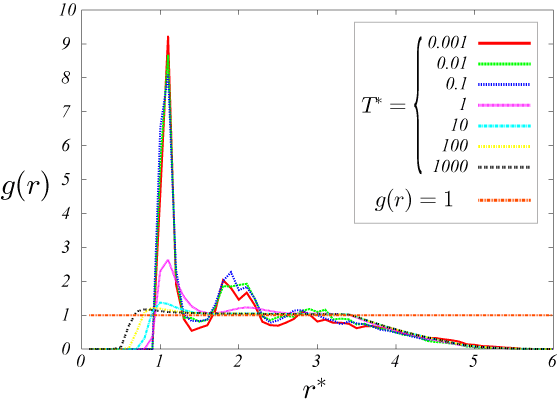
図４．\rho=0.4

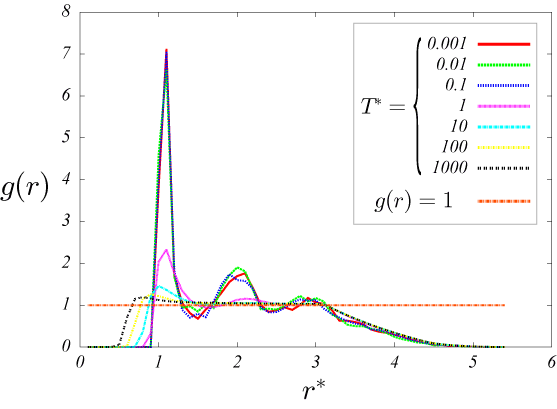
図５．\rho=0.5

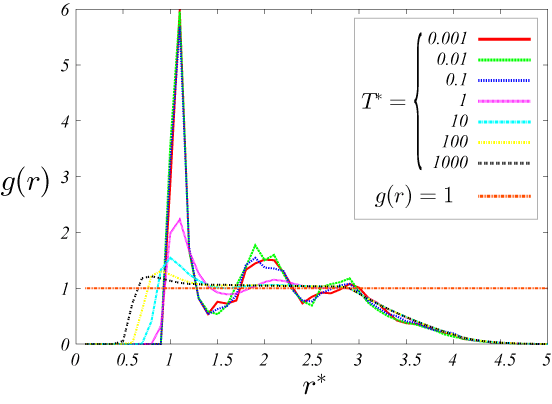
図６．\rho=0.6

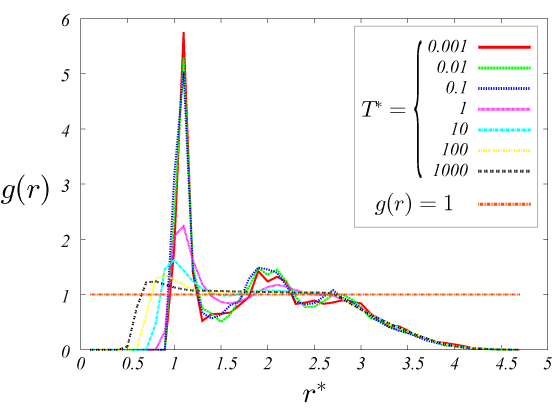
図７．\rho=0.7

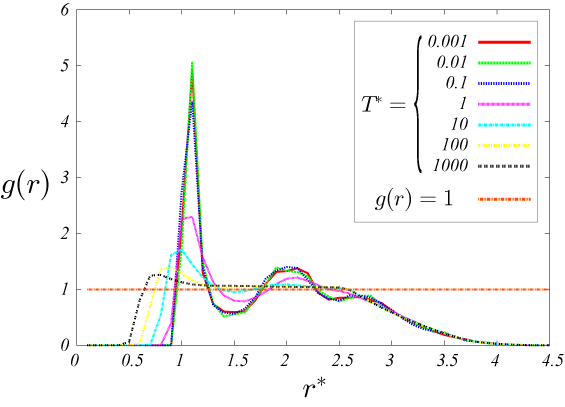
図８．\rho=0.8

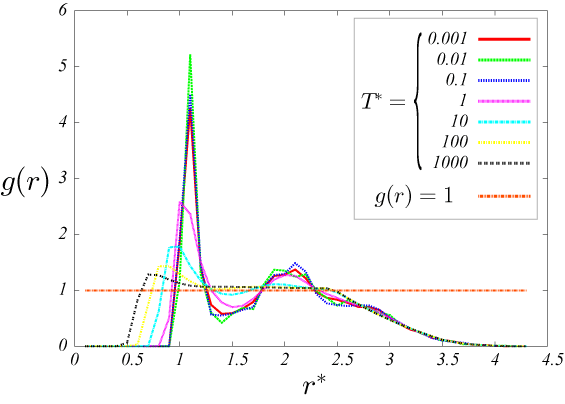
図９．\rho=0.9

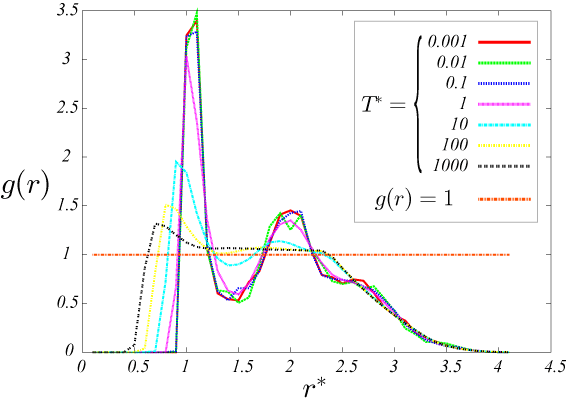
図１０．\rho=1.0

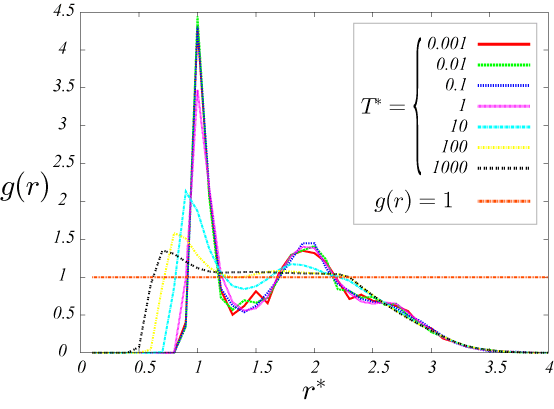
無次元温度一定の場合

温度が高くなるにつれ、動径分布が1に近づいていることが分かる。

図１１．T^*=0.001

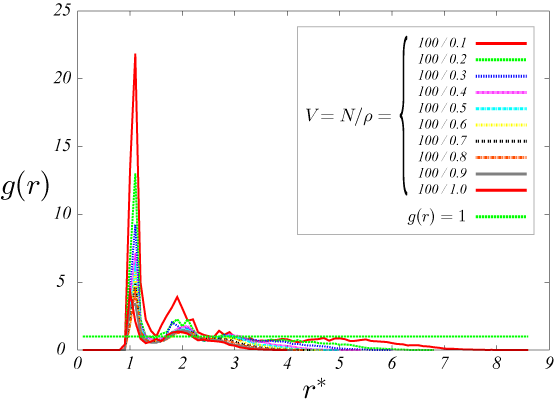
図１２．T^*=0.01

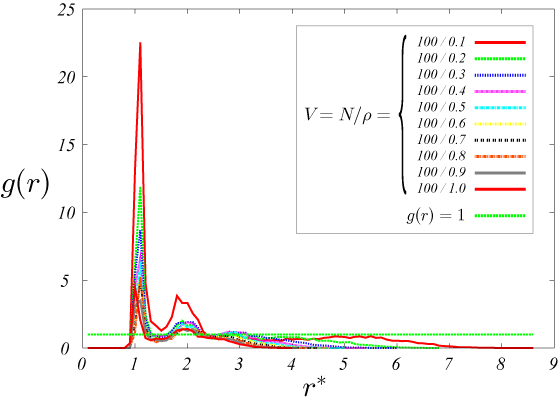
図１３．T^*=0.1

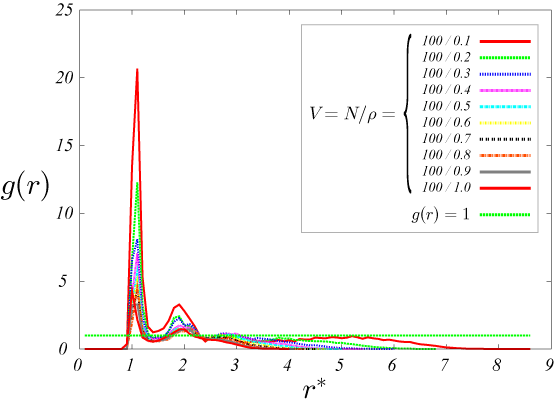
図１４．T^*=1.0

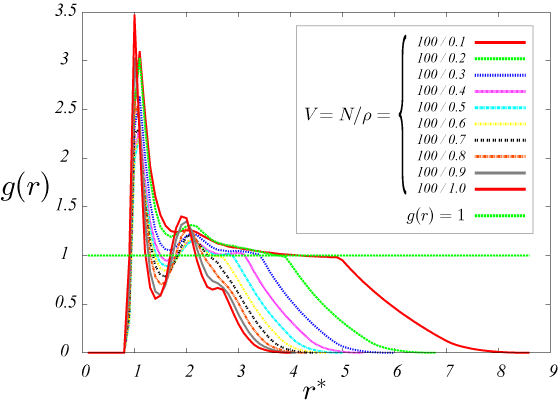
図１５．T^*=10

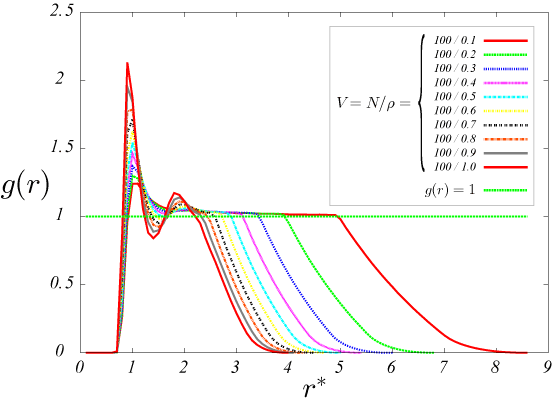
図１６．T^*=100

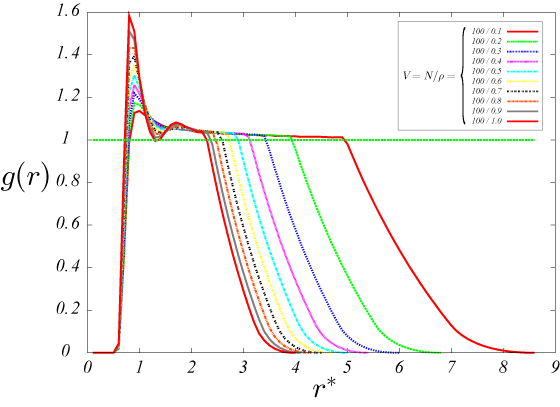
図１７．T^*=1000

計算精度について

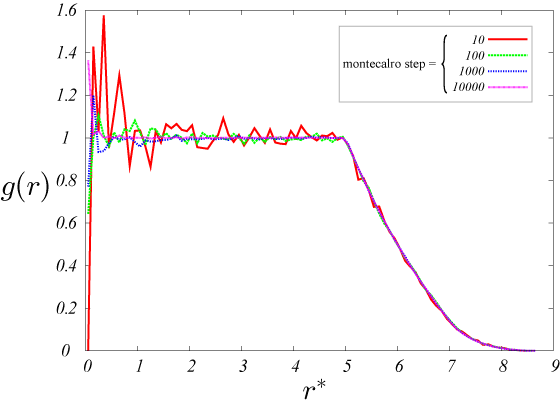
モンテカルロシミュレーションで妥当な計算結果を得るためのステップ数（モンテカルロステップ）について考察する。 下の計算結果は、理想気体の場合の動径分布をモンテカルロステップ(ms)＝10,100,1000,10000 の場合について計算した。
理想気体の場合、動径分布関数は r に依らず g(r)=1 となるはずである。 msが大きくなるにつれ、r=0 付近以外で g(r)=1 に近づいていることが分かる。
ms = 10000 のでは、g(r)=1 からのずれは1%程度となっている。r の小さな領域で誤差が大きな理由は、g(r)を求めるときに 小さな r での割り算があるためであることが考えられる。 但し、レナード・ジョーンズポテンシャルの場合には元々、r の小さな領域では g(r)=0 であるために、割算による誤差が生まれない。

図１８．理想気体の場合

今後の予定

・圧縮因子 Z の計算を行う
・静的分布関数を計算を行う