DLAシミュレーション１（VisualC++ ＋ DirectX で描画）

DLAとは

拡散律則凝集と和訳される DLA（diffusion-limited aggregation）とは、

１．システムの中央に結晶の核がある
２．粒子が遠方からブラウン運動をしながら、近づいてくる
３．中央にある結晶の核に隣接すると、粒子は結晶化する
４．以後は同様に、ブラウン粒子が結晶化された粒子に隣接すると結晶化する
５．１度に１つのブラウン粒子が運動をする

というモデルである。 今回、DirectX でリアルタイムの描画を行なうのであるが、 結晶成長に時間がかかるので、上記の５を無視して、粒子数を10000としてシミュレーションを行った。

２次元の例

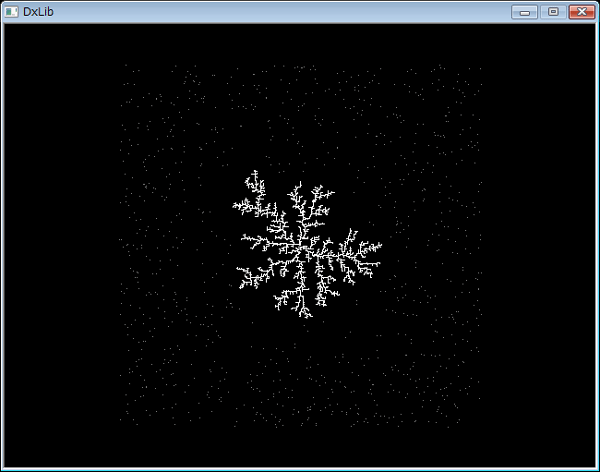
スナップショット

結晶化した粒子にブラウン粒子が隣接した際の結晶化する率を今回は「1」で計算している。

VisualC++ ＋ DirectX のソース

※DirectXの利用の仕方はこちらをご覧ください。
注意：以下のソースには、無駄なインクルードがあります。

#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include "mt19937ar.h"

#include <cstdio>
#include <iomanip>
#include <stdio.h>
#include <direct.h>
#include "DxLib.h"
using namespace std;

double PI = 3.14159265358979323846;
double e = 2.7182818284590452354;
int width = 640;
int height = 480;
//備考：画面サイズはデフォルトで、640×480

int dimension = 2;
int core_number = 0; // 固まった数
int N_max = 100000;
bool go = true;
bool core[20001][20001] = {false}; 
int core_[10000][2] = {0}; 
int x_0 = 10000;
int y_0 = 10000;
double R = 100.0;
double r = 1.0;

//核の座標
class Perticle{
public:
	int D[10];//10次元までの座標
	Perticle(){
		for(int j=0; j<dimension; j++ ){
			D[j] = 0;
		}
		double theta=2.0*PI*genrand_real1();
		D[0]= int(R*cos(theta));
		D[1]= int(R*sin(theta));
	}
    void Step(){
		int nn = int(dimension * genrand_real1());
		if(genrand_real1()>0.50) D[nn]++;
		else D[nn]--;
		if(D[0]<0 - int(R)) D[0] += 2*int(R);
		if(D[0]>0 + int(R)) D[0] -= 2*int(R);
		if(D[1]<0 - int(R)) D[1] += 2*int(R);
		if(D[1]>0 + int(R)) D[1] -= 2*int(R);
	}
    void Restart(){
		double theta=2.0*PI*genrand_real1();
		D[0]= int(R*cos(theta));
		D[1]= int(R*sin(theta));
	}
};

// プログラムは WinMain から始まります
int WINAPI WinMain( HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow )
{
	init_genrand((unsigned)time(NULL));
	Perticle p[1000];

	core[10000][10000]= true;
	core_[0][0] = 0;
	core_[0][1] = 1;

	//メインループ
	ChangeWindowMode(TRUE);
	if( DxLib_Init() == -1 ) return -1 ;  // ＤＸライブラリ初期化処理
	while(ProcessMessage()==0 && CheckHitKey(KEY_INPUT_ESCAPE)==0){
		ClsDrawScreen();

		//核の描画
		for(int i=0; i<=core_number; i++){
			DrawPixel( core_[i][0] + width/2 , core_[i][1] + height/2 ,GetColor(255,255,255) ) ;
		}
		for(int i=0; i<1000; i++){
			p[i].Step();
			DrawPixel( p[i].D[0]  + width/2 , p[i].D[1] + height/2 , GetColor(122,122,122) ) ;

			if(core[x_0+p[i].D[0]+1][y_0+p[i].D[1]] == true || core[x_0+p[i].D[0]-1][y_0+p[i].D[1]] == true || core[x_0+p[i].D[0]][y_0+p[i].D[1]+1] == true || core[x_0+p[i].D[0]][y_0+p[i].D[1]-1] == true ){
				core_number++;
				core[x_0+p[i].D[0]][y_0+p[i].D[1]] = true;
				core_[core_number][0] = p[i].D[0];
				core_[core_number][1] = p[i].D[1];
				if(pow(double(p[i].D[0]),2)+pow(double(p[i].D[1]),2) > pow(r,2)){
					r = sqrt(pow(double(p[i].D[0]),2)+pow(double(p[i].D[1]),2));
					R = r + 100.0;
				}
				p[i].Restart();
			}

		}
		ScreenFlip();
	}

	DxLib_End() ;  // ＤＸライブラリ使用の終了処理

	return 0 ;  // ソフトの終了 
}

今後の予定

・結晶化率を変化させたときの、変化を調べる
・N次元DLAにおけるフラクタル次元の計算を行う。