DLAシミュレーション２

ブラウン運動している粒子（ブラウン粒子）が、結晶化している粒子の隣に来たときに結晶化する率（吸着率）を変化させて、 結晶成長の吸着率依存性についてシミュレーションしてみる。
（※DLAについてはこちら）

計算結果

粒子数＝100,000
吸着率＝1, 0.1
以上の計算結果を以下に掲載する

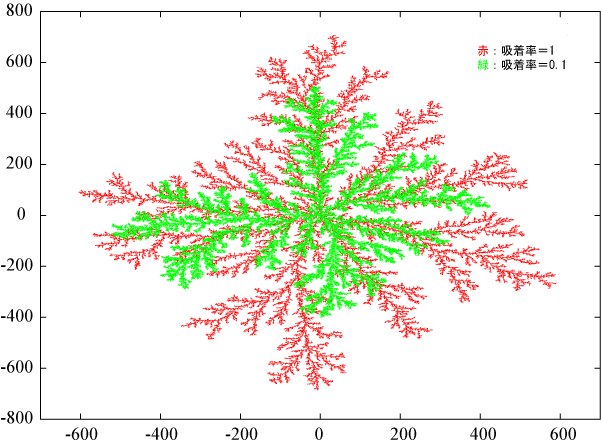
吸着率が0.1のほうが、ブラウン粒子は中心部までたどりつきやすいので、全体的に太ったようになる。

VisualC++ ＋ DirectX のソース

注意：以下のソースには、無駄なインクルードがあります。

#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include "mt19937ar.h" //メルセンヌ・ツイスタ
#include <cstdio>
#include <iomanip>
#include <stdio.h>
#include <direct.h>
using namespace std;

double PI = 3.14159265358979323846;
double e = 2.7182818284590452354;
//備考：画面サイズはデフォルトで、640×480

int dimension = 2;
int core_number = 0; // 固まった数
int N_max = 100000;
bool core[20001][20001] = {false}; //中心座標(0.0)＝配列中心[10000][10000]
int x_0 = 10000;
int y_0 = 10000;
double R = 200.0;
double r = 1.0;

//核の座標
class Perticle{
public:
  int D[10];//10次元までの座標
  Perticle(){
    for(int j=0; j<dimension; j++ ){
      D[j] = 0;
    }
    double theta=2.0*PI*genrand_real1();
    D[0]= int(R*cos(theta));
    D[1]= int(R*sin(theta));
  }
    void Step(){
    int nn = int(dimension * genrand_real1());
    double pp= genrand_real1();
    if(pp>0.50) D[nn]++;
    else D[nn]--;
    if(core[x_0+D[0]][y_0+D[1]]==true){//排除体積効果
      if(pp>0.50) D[nn]--;
      else D[nn]++;
    }
    if(D[0]<0 - int(R)) D[0] += 2*int(R);
    if(D[0]>0 + int(R)) D[0] -= 2*int(R);
    if(D[1]<0 - int(R)) D[1] += 2*int(R);
    if(D[1]>0 + int(R)) D[1] -= 2*int(R);
  }
    void Restart(){
    double theta=2.0*PI*genrand_real1();
    D[0]= int(R*cos(theta));
    D[1]= int(R*sin(theta));
  }
};

int main(){
  init_genrand((unsigned)time(NULL));
  string current_s,folder_s;
  current_s = "D:/DLA/result/D2/";//計算結果フォルダの場所
  _mkdir(current_s.c_str());

  for(int n=1; n>0;n--){
    core_number = 0;
    r=1.0;
    R=200;
    // コアの初期化
    for(int i =0; i<=20000;i++){
      for(int j=0; j<=20000;j++){
        core[i][j] = false; 
      }
    }
    double probability = 0.1* double(n);//接触時の吸着確率
    ostringstream foldername;
    foldername <<  "DLA-" << n << ".data";
    folder_s = foldername.str();
    folder_s = current_s + folder_s;
    ofstream fout_position;
    fout_position.open(folder_s.c_str());

    Perticle p[1];

    core[10000][10000]= true;
    cout << core_number <<" "<< 0 << " " << 0 <<" r=" << r << endl;
    fout_position  << 0 << " " << 0  << endl;

    while(core_number<=N_max){
      for(int i=0; i<1; i++){
        p[i].Step();
        if(core[x_0+p[i].D[0]+1][y_0+p[i].D[1]] == true || core[x_0+p[i].D[0]-1][y_0+p[i].D[1]] == true || core[x_0+p[i].D[0]][y_0+p[i].D[1]+1] == true || core[x_0+p[i].D[0]][y_0+p[i].D[1]-1] == true ){
          if(probability>genrand_real1()){
            core_number++;
            core[x_0+p[i].D[0]][y_0+p[i].D[1]] = true;
            if(pow(double(p[i].D[0]),2)+pow(double(p[i].D[1]),2) > pow(r,2)){
              r = sqrt(pow(double(p[i].D[0]),2)+pow(double(p[i].D[1]),2));
              R = (r+200.0)*2.0;
            }
            fout_position << p[i].D[0] << " " <<  p[i].D[1] << endl;
            cout << "n=" << n << " " << core_number << " " << p[i].D[0] << " " << p[i].D[1] << " r=" << r << endl;
            p[i].Restart();
          }
        }

      }
    }
    fout_position.close();
  }
}

今後の予定

・吸着率に対するフラクタル次元を計算する