金属の凝固を知る
鋳造工学における基礎知識についてまとめる
溶融金属の流れ制御
液体金属の流れを理解する目的は以下の通りである。
- ・鋳造中に液体金属内に空気を入れないようにする
- ・介在物を混合しないようにする
- ・鋳型の隅々まで湯を流す
流体の理解
流体の運動を理解する上で欠かせない物理量としては以下が挙げられる
- ・粘性(粘性係数 )
- ・慣性(代表として密度ρ)
上記から動粘性係数ιを以下のように定義する。
![]()
流体の運動はレイノルズ数で議論する。レイノルズ数とは慣性力と粘性力との比で定義される無次元数である。流体力学において流れの性質を調べるために利用される重要な値である。 モデル実験をする場合は相似形でかつレイノルズ数をそろえて行う。 また重力を考慮する際にはフルード数、表面張力を考慮する場合はウェーバー数もそろえる。
理想流体
粘性がゼロ、つまり流れるうちにエネルギー損失のない流体を理想流体として考える。理想流体では
運動エネルギー+位置エネルギー+圧力=一定
である。例えば低いところを流れれば位置エネルギーが減った分だけ運動エネルギーが増える。狭いところを通過すれば運動エネルギーが増えると圧力が減る。砂型のように通気性のある鋳型の中の湯道などで流速が速くなりすぎると圧力が大気圧より低くなり溶融金属中に空気が吸い込まれる可能性がある。
このような関係を定量的に書いたものがベルヌイの定理である。
![]()
E0が単位体積の初期エネルギーの値でそれがどこまでも保存されることを示している。 また、水槽の上面では速度が0に近いので
![]()
下の出口では高さがゼロだが速度と圧力の項があるので
![]()
式(1),(2)のEが等しいことから流速vが求まる。
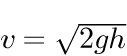
これがトムチェリの定理である。これによると流速vは流体の密度、経路によらない。したがって流量は出口面積Aに比例してAvとなることが予想できる。このようにトムチェリの定理は大まかな見積もりに役立つ式である。
流れ抵抗
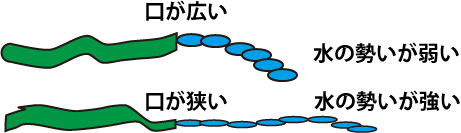
トムチェリの式で説明できない場合が存在する。例えばホースの口を閉じると水が勢いよく水が出てくる。これは流速vが長さや断面積によらないというトムチェリの式に矛盾する。これは流路の抵抗のためエネルギー損失が起こりその損失量が流速が大きいほど大きい。 理想流体では起こらない損失項を加えて補正したベルヌイの式で計算すると良い。
流動性と薄肉鋳造
転写性,流動性
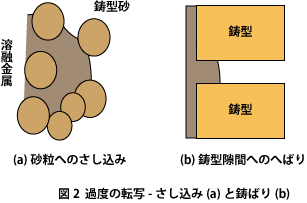
転写性とは鋳型孔に液体金属を充填しそこで凝固させて孔の形状をそっくり写しとった形状を作ることである。用湯が流れている途中で凝固せず、かつ参加しないようにする必要がある。 よって、流動性が良い条件は鋳込み温度が高い、流速が速い、鋳型の熱吸収能力が低い、純金属または共晶点を選ぶとよい。
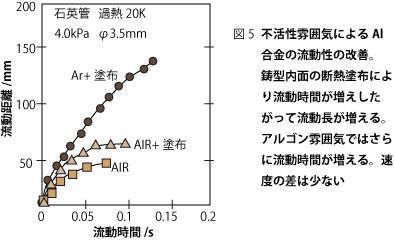
薄肉鋳造
鋳物をできるだけ薄肉にし軽量化することは鋳物業界の大切な課題の一つである。 薄肉化に伴う技術問題の一つに流動性が上げられる。流動性を良くするための条件は先ほどの通り。 しかし、アルミホイールなどの低圧鋳造の鋳型内の空気をアルゴンで置換することによって酸化物が減るだけでなく流動性も良くなるという実験事実がある(日立金属大西グループ)。 不活性雰囲気によって鋳型流布剤が燃焼しにくくなり断熱効果が長持ちするためだろうという結論は出たがわからない点も多くある。このように今後も基礎研究を進める余地は多分にある。 薄肉鋳造では凝固速度が支配的で表面張力や粘性は余り問題にならないことがわかっている。