HOME > natural science Laboratory > ロボティクス講座 > LabVIEW TIPS集

ロジスティック写像の点列の存在確率

文責：佐瀬 一弥 （2009年7月12日） カテゴリ：LabVIEW TIPS集(47)

ロジスティック写像x_{n+1}=ax_n(1-x_n)の分岐図には網目が重なるように 濃淡がみられる。 濃い部分はx_nの存在確率が高いと言える。 分岐図を何度かいても、この濃淡は 同じになることから、aの値がわかっているとき、 x_nの値がいくつであるかを存在確率でこたえることができる。
aを一定にし、10万個のx_nを作ったときのx_nの確率分布を 生成するプログラムをLabVIEWで作ってみた。
プログラムはこちら。
probability_distribution.vi


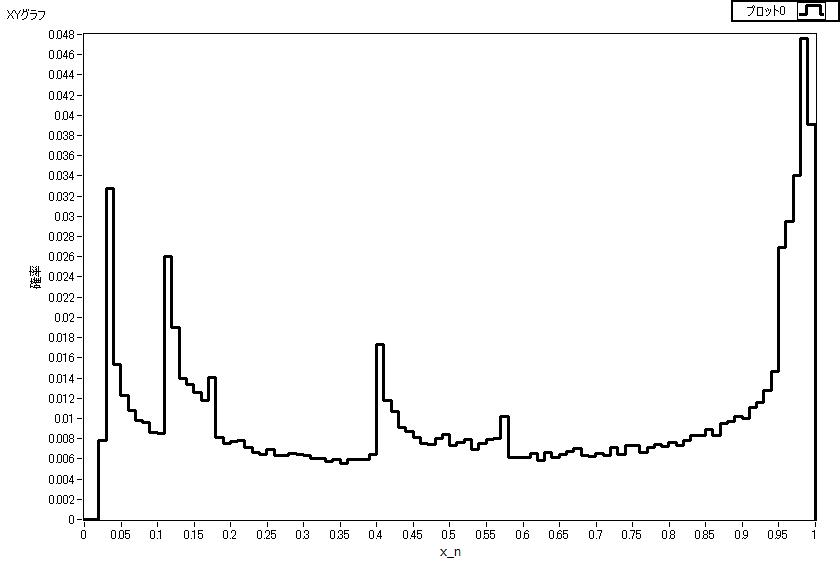
a=3.97のときの点x_nの存在確率


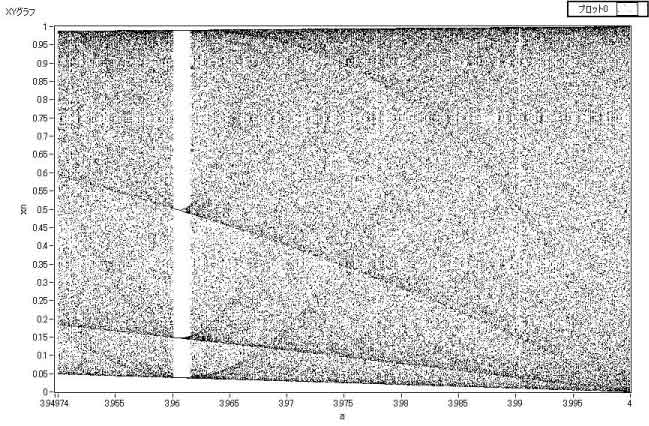
分岐図の拡大図 a=3.97に 注目すると、網目が重なっっているところと上の図の存在確率が高いところが 一致していることが分かる。



▲このページのトップ ｜ NPO法人 natural science トップ

▲このページのトップ ｜ NPO法人 natural science トップ




Warning: mysqli_connect(): (28000/1045): Access denied for user 'xsvx1015071_ri'@'sv102.xserver.jp' (using password: YES) in /home/xsvx1015071/include/natural-science/include_counter-d.php on line 8
MySQL DBとの接続に失敗しました