台形公式とシンプソンの公式を使っての積分誤差を確かめる（C言語）

数値積分で計算誤差を確かめてみるために、台形公式とシンプソンの公式を使って、sin の積分の誤差を刻み幅を変えて計算してみた。

計算結果

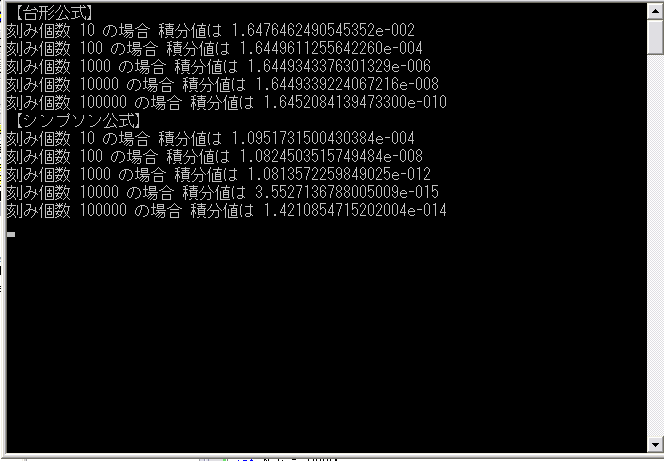
ソース（台形公式・シンプソンの公式）

/*
積分の計算(台形公式とシンプソン法)
　積分区間[0,PI]
　被積分関数 f(x) =sin(x)
　理論値 2
*/
#include <math.h>
#include <stdio.h>

double PI = acos(-1.0);
double f(double);
double Trapezium(double ,double ,int);
double Simpson(double ,double,int);

int main (void){

	printf("【台形公式】\n");
	for(int n=1; n<=5 ; n++){
		int kizami = int(pow(10.0,n));
		double gosa = abs(Trapezium(0.0,PI,kizami) - 2.0);
		printf("刻み個数 %d の場合 積分値は %.16e\n",kizami, gosa );
	}
	printf("【シンプソン公式】\n");
	for(int n=1; n<=5 ; n++){
		int kizami = int(pow(10.0,n));
		double gosa = abs(Simpson(0.0,PI,kizami) - 2.0);
		printf("刻み個数 %d の場合 積分値は %.16e\n",kizami, gosa );
	}

return 0;
}
double f(double a)
{
	return sin(a);
}
double Trapezium(double a ,double b ,int N)
{
	double c =0.0;
	for(int i=1; i<=N-1; i++){
		double x = a + (b-a)/double(N) *double(i);
		c += f(x);
	}
	return (b-a)/double(N) * ( (f(a)+f(b))/2.0 + c );
}
double Simpson(double a ,double b ,int N)
{
	double ss1 =0.0;
	for(int i=1; i<=N/2-1; i++){
		double x = a + (b-a)/double(N) * double(2*i);
		ss1 += f(x);
	}
	double ss2 =0.0;
	for(int i=1; i<=N/2; i++){
		double x = a + (b-a)/double(N) * double(2*i-1);
		ss2 += f(x);
	}
	return  (b-a)/(3.0*double(N)) * ( f(a)+f(b) + 2.0 * ss1 + 4.0 * ss2 );
}