積分区間に変数が入る２重積分の数値計算（シンプソン法 C++）

積分区間が矩形であれば、先日の等間隔シンプソン法が非常に精度が高いが、
次のような、積分区間に変数となる２重積分の数値計算はできない。
１次元のシンプソン法を改良するしかないのだろうか。

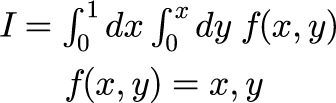
C++ソース

/*
１次元シンプソン法
例：f(x,y) = xy  x[0:1], y[0:x]
*/
#include <math.h>
#include <stdio.h>

double F(double x, double y);
double Simpson1_2(double x0, double x1, double y0, double y1 ,int N);

int main(void){

  double exa = 1.0/8.0;
  int kizami = 10000;
  double s = Simpson1_2(0, 1.0, 0, 1.0 , kizami) ;

  //結果の書き出し
  printf("  刻み数 : %d\n", kizami);
  printf("  積分値 : %22.15e\n", s);
  printf("  誤　差 : %22.15e\n", s - exa);

  return 0;
}
double F(double x, double y) //被積分関数
{
  return x*y;
}

double Simpson1_2(double x0, double x1, double y0, double y1 ,int N)
{
  int i, j;
  double x,y, c=0.0;
  double ss1 , ss2;
  
  for(i=0; i<=N; i++){
    x = x0 + (x1-x0)/double(N) * double(i);
    y1 = x;
    ss1 =0.0;
    for(j=1; j<=N/2-1; j++){
      y = y0 + (y1-y0)/double(N) * double(2*j);
      ss1 += F(x,y);
    }
    ss2 =0.0;
    for(j=1; j<=N/2; j++){
      y = y0 + (y1-y0)/double(N) * double(2*j-1);
      ss2 += F(x,y);
    }
    c += (y1-y0)/(3.0*double(N)) * ( F(x,y0)+F(x,y1) + 2.0 * ss1 + 4.0 * ss2 );
  }
  return  c * (x1-x0)/double(N);
}

実行結果