VisualC++ と OpenGL を利用した仮想物理実験室
【1-1-2】等速度直線運動のアルゴリズムの導出

文責：遠藤理平（2009年12月28日）カテゴリ：コンピュータ・シミュレーション講座授業日誌(81)｜仮想物理実験室(325)

「【1-1-1】物理量について」では、客観的かつ普遍的な量として物理量の概念を導入し、「時刻 t[s]」「位置 r[m]」を定義しました。次は、この２つの物理量を組み合わせて得られる物理量を定義します。

時刻 t_0 で位置 x_0 の球が、時刻 t_1 で位置 x_1 に運動している場合を想定します（下図）。

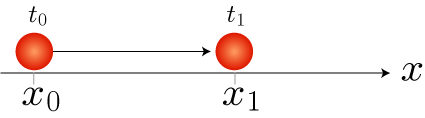
もし球が、t_0 から t_1 まで、等速度（同じ速度）で運動しているとすると、次の関係式が成り立ちます。

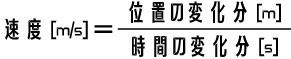
左辺の「速度」は、「時刻」と「位置」の２つの物理量を組み合わせて定義される新しい物理量です。

物理量２「速度」（1次元）

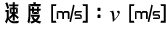
上記では等速度と仮定していますが、等速度でない場合は、平均の速度という物理量になります。次の図は、「時刻 t[s]」と「位置 x[m]」の関係をt-xグラフ（横軸t、縦軸x）で表したものです。

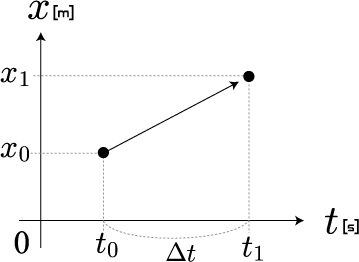
t-xグラフで表すと「速度」は傾きで表されます。つまり速度 v は次の関係式で表すことができます。

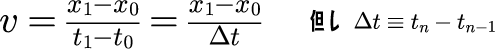
この関係式は、「時刻 t_0 のときの位置 x_0 と時刻 t_1 のときの位置 x_1 が与えられれば、速度 v[m/s] が得られる」ことを意味しています。Δt は、時刻 t_0 と t_1 との時間間隔（時間の変化分）を表しています。また、関係式を移項することで、次の関係式が得られます。

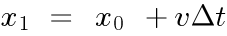
この関係式は「時刻 t_0 のときの位置 x_0 と速度 v が与えられていれば、Δt 秒後の位置 x_1 が得られる」を意味し、式変形により物理的な意味が変わります。物理学では、「右辺に原因（因）→左辺に結果（果）」として表現します。また、コンピュータ・プログラミングの世界でも同様の表現します。コンピュータ・シミュレーションでは、この因果関係を明示的に意識することが非常に重要になります。

上式は、位置 x_0 と x_1 との関係式ですが、一般的な位置 x_n と x_{n-1} との関係でも成り立ちます。

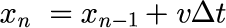
つまり「時刻 t_{n-1} のときの位置x_{n-1} と速度 v が与えられていれば、Δt 秒後の位置 x_n が得られる」ことを意味します。更にこれを発展させて、速度 v[m/s] が一定値のまま（等速度）であるならば、任意の時刻 t_n での位置 x_n は、x_0 からスタートして、x_1, x_2 ... x_nと逐次計算することで求めることができます。

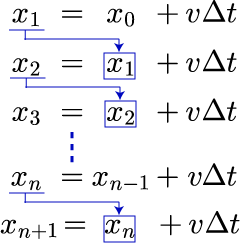
３次元の場合も同様に、速度 v[m/s] は速度ベクトルという物理量で定義することができます。

物理量２「速度」（3次元）：速度ベクトル

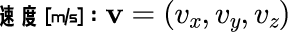
３次元の場合は、x 成分の他にy成分とz成分がそれぞれ同様に成り立ちます。

等速直線運動を逐次計算するアルゴリズム（オイラー法）

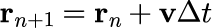
「r」は【１日目】物理量についてで登場した位置ベクトルです。