水の加熱のモデル構築
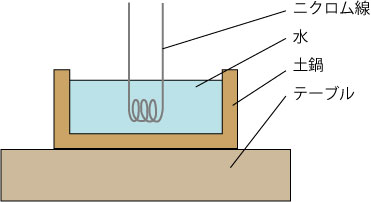
図1 実験装置の概略図
温泉たまご自動調理機の製作のために行った、ヒーターによる加熱と水の温度の変化
の実験の考察を行う。
実験装置の概略図を図1に示す。
土鍋に入った水をニクロム線で加熱し、温度センサICで水の温度を測定しPCに記録する。
(LabVIEWとデータ集録デバイスNI USB-6009を使用)
実験条件と結果
実験条件は以下の通り。
水の体積 400ml
消費電力 300W
室温 20℃
図2に結果を示す。(ロボティクス講座で測定)
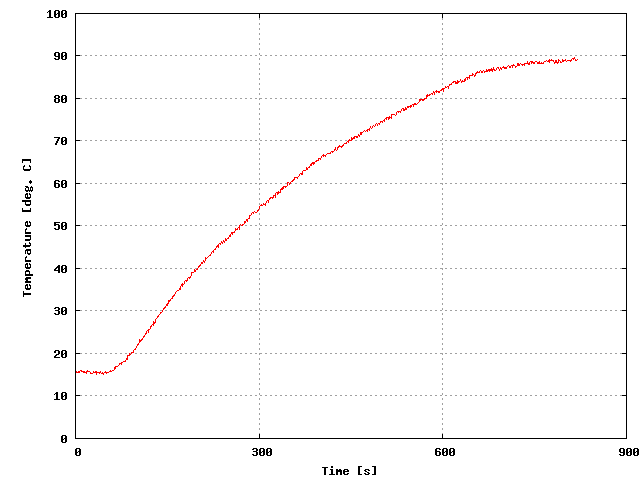
図2 水の温度変化(供給電力300W)
モデルと測定値の比較
以降では次の記号を用いる。
\dot{Q}_{in}:水に流入する単位時間当たりの熱量[J/s]
\dot{Q}_{out}:水から流出する単位時間当たりの熱量[J/s]
P:消費電力[W/s]
T_{water}:水の温度
T_{water0}:t=0のときの水の温度[℃]
C:熱容量[J/℃]
h:系の熱伝達率
モデル1
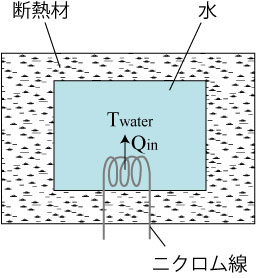
図3 モデル1
ニクロム線による熱がすべて水の温度上昇に寄与し、
水から熱が出ていかないモデルを考える。(図3)
ニクロム線から水に与えられる単位時間当たりの熱量[J/s]は、次式で与えられる。
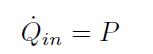
熱は外へ出ていかないので、水の温度変化は次式となる。
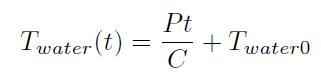
モデル2
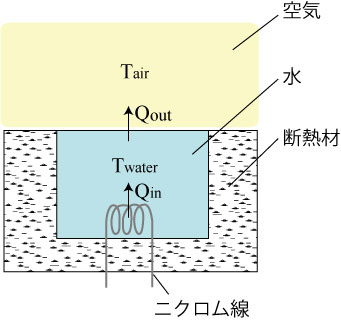
図4 モデル2
ニクロム線から熱を与えられ、水と空気が熱のやり取りをするモデル
を考える(図5)。以下の仮定のもと式を導出する。
・水は空気とニクロム線とのみ熱をやり取りする
・ニクロム線における消費電力はすべて水の温度上昇に寄与する熱になる。
・水の温度分布は常に均一である。
・水から空気へ移動する熱は空気の温度と水の温度の差に比例する。
ただし、空気の温度は、水の表面から十分に離れた位置の温度(室温)とし、
室温は変化しない。
ニクロム線から水に流入する単位時間当たりの熱量[J/s]は次式で与えられる。
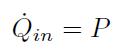
水から空気へ流出する単位時間当たりの熱量[J/s]は次式で与えられる。
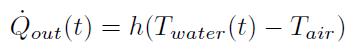
水の温度変化は次式で表わされる。
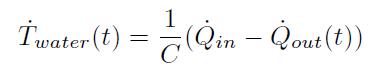
上の3式を連立して整理すると、次の微分方程式を得る。
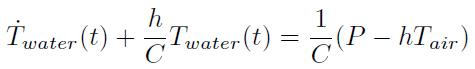
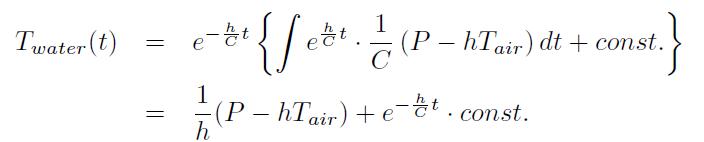
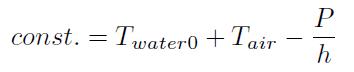
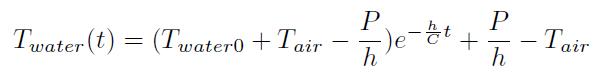
モデルと測定値の比較
上記の実験条件における、それぞれのモデルと測定値の比較を図5に示す。 ただし、モデル2のhは未知であり、図はh=1とした場合である。実験開始から100sほどでは、測定値は温度がほとんど上昇していない。これは水がニクロム線の付近から温度が上昇するが、測定位置で測定されるまで遅れが生じることが原因と思われる。 モデルでは水の温度がいたるところで一定と仮定したので、測定の遅れは表わせていない。
モデル1の傾きは測定値の100s付近の傾きとほとんど一致しており、 温度が室温に近い時のおおまかな挙動を表わせそうである。
モデル2は温度が上がるにつれて温度の傾きが小さくなっていく様を表わせているが、温度が大きくなるにつれて、測定値との差が開いていく。
高温でも適用可能なモデルの構築のために、沸騰による熱の流出も考慮が必要と思われる。
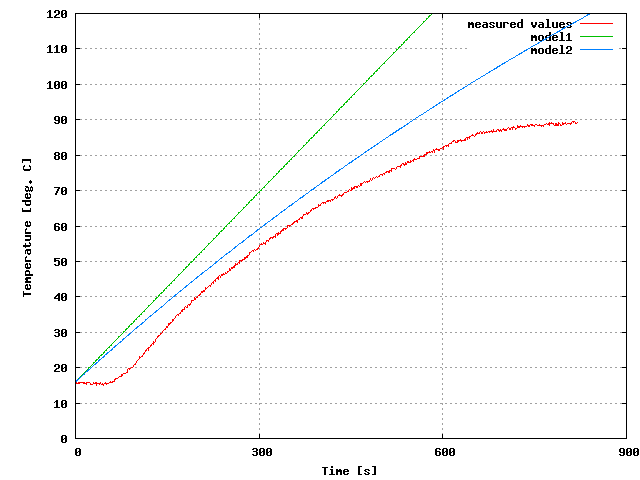
図5温度の時間変化の測定値とモデルの比較