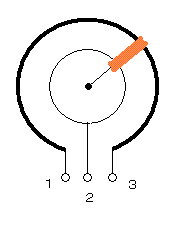【2010.07.29】
可変抵抗のブラックボックスを開いてみた。

可変抵抗のプリントに関連して。
可変抵抗とは、つまみを回すことで、抵抗の持つ抵抗値を変化させることのできるものである。
仕組みについて非常に気になったので、簡単に調べてみた。
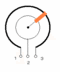
手元にある可変抵抗は、下図写真に示したものだけであった。
これを題材にして可変抵抗の仕組みを知りたい。


まずは、この可変抵抗の足について。
可変抵抗は基本的に、写真上の１番と２番、または１番と３番を回路に繋いでいくことになる。
１番と２番、３番と２番のように、２番が必ず回路に接続されることから、この可変抵抗は、１番と３番の中点と２番を通る直線に対して対称であることが容易に予想される。つまり、この対称性から１番２番をつなぐ場合のみを考察すればよい。
次に、どうして１番と３番では抵抗値が変わらないのかという疑問から解決する。

◎測ってみた。
（i）つまみの矢印が一番左を指すとき[0度]
１番３番　＊　4.64 kΩ　
１番２番　＊　0.00 kΩ
（ii）つまみの矢印が真ん中を指すとき[120度]
１番３番　＊　4.63 kΩ
１番２番　＊　2.23 kΩ
(iii)つまみの矢印が一番右側を指すとき[240度]
１番３番　＊　4.65 kΩ
１番２番　＊　4.65 kΩ

このことからわかるのは、おそらく、つまみの回転角に比例して、１番２番の抵抗値が変化する仕組みだということがわかる。また、１番３番が回転角に依存しないことから、つながっているものと考えられる。

おっと。



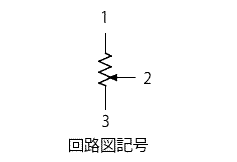
ここで、ふと気がついたのだが、回路図記号と比較すると、１番３番がつながっていて、２番を動かして抵抗値を変えていることは一目瞭然であった。ここまでの考察は無駄だったか？

では、２番を動かす仕組みは？
回路図記号とを見つめるに、２番を動かすというより、２番と１－３間をつなぐ矢印を動かしているようである。ここで閃いた。
「時計か・・・。」時計のようにくるくる矢印が回る仕組みである。
そういえば、去年の防衛医科大の入試問題に似た問題があったことを思い出した。そうか。去年のあの問題は、可変抵抗が題材だったのか。
大学入試問題はやっぱりよく練られた問題が出ていると改めて思う。


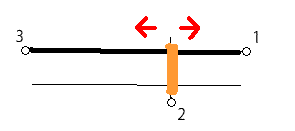
図にすると、こんな感じ（上図）だろうか。
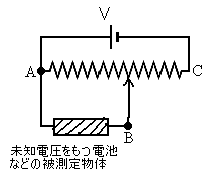
おそらく、直線型のスライドスイッチのような可変抵抗も存在すると考えられる。高校の勉強で出現し、よく入試問題にも採用される「メートルブリッジ」（下図）にも現れている。

手元にある、この青い可変抵抗は、配置する場所のスペースを考えて小さく設計されたものでありそうだ。
したがって、直線型の可変抵抗（二つ上の図）をくるっと丸めればよい。

先程測ってみた可変抵抗の抵抗値について、無駄にはしたくないので、ここで考察に利用する。
上図において、確かに１番と３番はつながっていて、つまみの回転角に依存しない。また、１番と２番において、確かに回転角に比例することがわかる。
ほんとはもう少し、書き足したかったが、時間もなくなってきたのでここでおしまい。
つぎは調べるとしたらトランジスタかな？
ありがとうございました。