VisualC++ と OpenGL を利用した仮想物理実験室
ラグランジュ運動方程式２：極座標を用いた球面振子

拘束条件を取り扱う場合，一般化座標を導入したラグランジュ運動方程式を解くことで取り扱うことができます。 前回は、ラグランジュ運動方程式のの一つ目の例として単振子のシミュレーションを行いました。 二つ目の例として極座標を用いた球面振子のシミュレーションを行います。

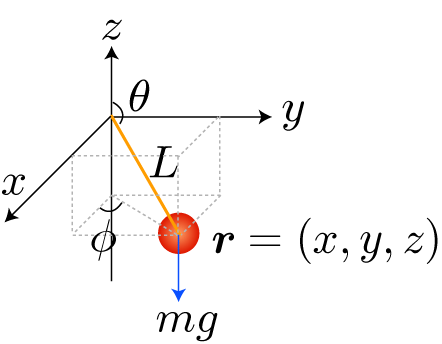
単振子の場合には一般化座標はθ一つでしたが、 球面振子の場合は、球面の上の1点を指定するのに自由度が2つあるので、 一般化座標はθとφが必要になります。

位置rを時刻 t で微分するとことで、速度位置vが得られます。

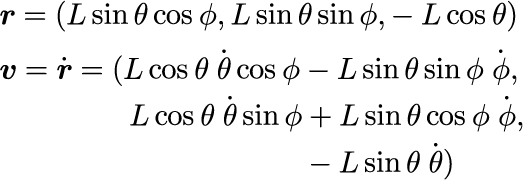
運動エネルギー T とポテンシャルエネルギーV 、ラグラジアンはそれぞれ次のように得られます。

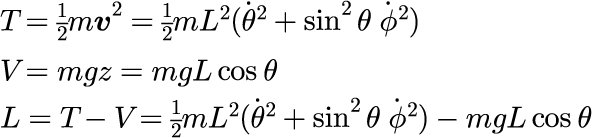
これにより，ラグランジュ運動方程式

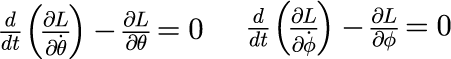
から，一般化座標θの満たすべき方程式が導かれます。

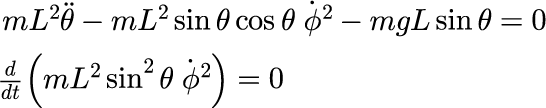
シミュレーションを行うため，数値計算法としてルンゲクッタ法を利用します。 ルンゲクッタ法を用いるために，次のように変形します．

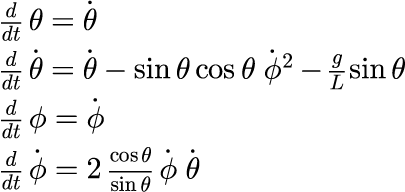
極座標を用いた単振子＋ルンゲクッタ法のアニメーション

極座標を用いた単振子＋ルンゲクッタ法のプログラム

【0-2-3】仮想物理実験室の構築 （ver1.2）を参照ください

構造体の定義

// ボールの定義
double ball_r = 4.0;//ボールの半径
struct BALL {
  double theta , theta_d;
  double phi , phi_d;
  double x, y, z;
  double l;
};
const int N = 3;

BALL ball[N];
void SetUp(void){
  for(int i=0; i<N; i++ ){
    ball[i].l       = L/double(N) * double(N-i);
    ball[i].theta   = 30.0/180.0 * PI * (i+3);    //
    ball[i].theta_d = 0,0;
    ball[i].phi     = 0.0;   
    ball[i].phi_d   = PI/20.0 *double(N-i);
  }
}

ルンゲクッタ法を利用した数値計算

/////////////////////////////////////////////
// ルンゲクッタ
double f1(double t,double theta,double theta_d, double phi,double phi_d, double l){
  return theta_d;
}
double f2(double t,double theta,double theta_d, double phi,double phi_d, double l){
	return sin(theta)*cos(theta)*pow(phi_d,2) + g/l * sin(theta);
}
double f3(double t,double theta,double theta_d, double phi,double phi_d, double l){
  return phi_d;
}
double f4(double t,double theta,double theta_d, double phi,double phi_d, double l){
  return - 2.0 * cos(theta) /sin(theta) * theta_d * phi_d;
}
void RungeKutta4(BALL *ball){
  double k1[4],k2[4],k3[4],k4[4];
  double theta   = ball -> theta;
  double theta_d = ball -> theta_d;
  double phi     = ball -> phi;
  double phi_d   = ball -> phi_d;
  double l       = ball -> l;
  k1[0]=dt*f1(t,theta,theta_d,phi,phi_d, l);
  k1[1]=dt*f2(t,theta,theta_d,phi,phi_d, l);
  k1[2]=dt*f3(t,theta,theta_d,phi,phi_d, l);
  k1[3]=dt*f4(t,theta,theta_d,phi,phi_d, l);
  k2[0]=dt*f1(t+dt/2.0,theta+k1[0]/2.0,theta_d+k1[1]/2.0,phi+k1[2]/2.0,phi_d+k1[3]/2.0, l);
  k2[1]=dt*f2(t+dt/2.0,theta+k1[0]/2.0,theta_d+k1[1]/2.0,phi+k1[2]/2.0,phi_d+k1[3]/2.0, l);
  k2[2]=dt*f3(t+dt/2.0,theta+k1[0]/2.0,theta_d+k1[1]/2.0,phi+k1[2]/2.0,phi_d+k1[3]/2.0, l);
  k2[3]=dt*f4(t+dt/2.0,theta+k1[0]/2.0,theta_d+k1[1]/2.0,phi+k1[2]/2.0,phi_d+k1[3]/2.0, l);
  k3[0]=dt*f1(t+dt/2.0,theta+k2[0]/2.0,theta_d+k2[1]/2.0,phi+k2[2]/2.0,phi_d+k2[3]/2.0, l);
  k3[1]=dt*f2(t+dt/2.0,theta+k2[0]/2.0,theta_d+k2[1]/2.0,phi+k2[2]/2.0,phi_d+k2[3]/2.0, l);
  k3[2]=dt*f3(t+dt/2.0,theta+k2[0]/2.0,theta_d+k2[1]/2.0,phi+k2[2]/2.0,phi_d+k2[3]/2.0, l);
  k3[3]=dt*f4(t+dt/2.0,theta+k2[0]/2.0,theta_d+k2[1]/2.0,phi+k2[2]/2.0,phi_d+k2[3]/2.0, l);
  k4[0]=dt*f1(t+dt/2.0,theta+k3[0],theta_d+k3[1],phi+k3[2],phi_d+k3[3], l);
  k4[1]=dt*f2(t+dt/2.0,theta+k3[0],theta_d+k3[1],phi+k3[2],phi_d+k3[3], l);
  k4[2]=dt*f3(t+dt/2.0,theta+k3[0],theta_d+k3[1],phi+k3[2],phi_d+k3[3], l);
  k4[3]=dt*f4(t+dt/2.0,theta+k3[0],theta_d+k3[1],phi+k3[2],phi_d+k3[3], l);
	ball->theta   = ball->theta   + (k1[0]+2.0*k2[0]+2.0*k3[0]+k4[0])/6.0;
	ball->theta_d = ball->theta_d + (k1[1]+2.0*k2[1]+2.0*k3[1]+k4[1])/6.0;
	ball->phi     = ball->phi     + (k1[2]+2.0*k2[2]+2.0*k3[2]+k4[2])/6.0;
	ball->phi_d   = ball->phi_d   + (k1[3]+2.0*k2[3]+2.0*k3[3]+k4[3])/6.0;
}