【波動論1】
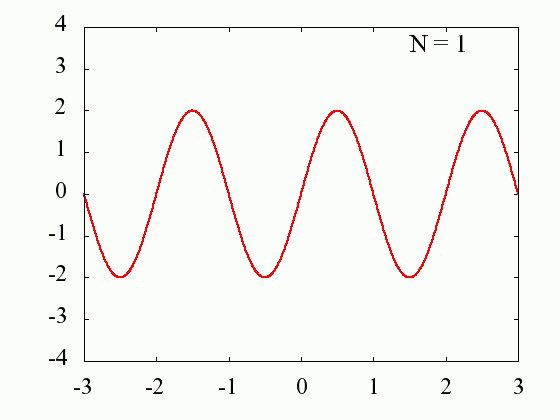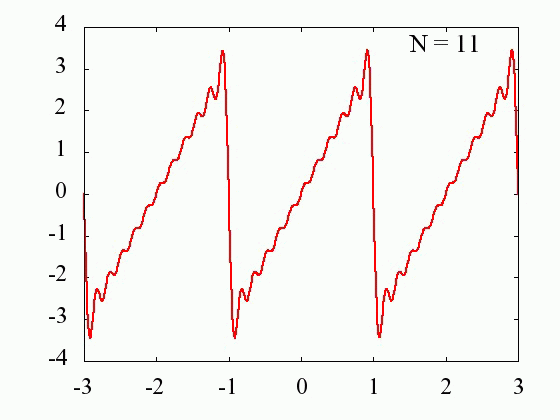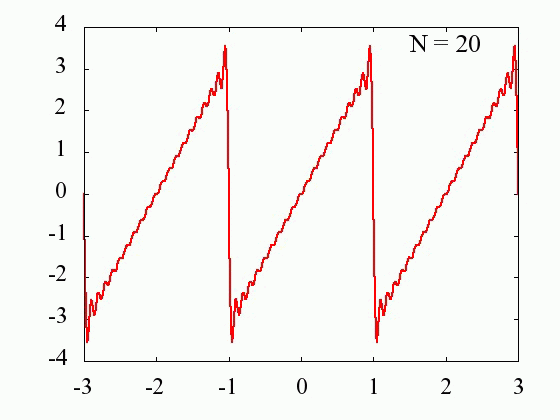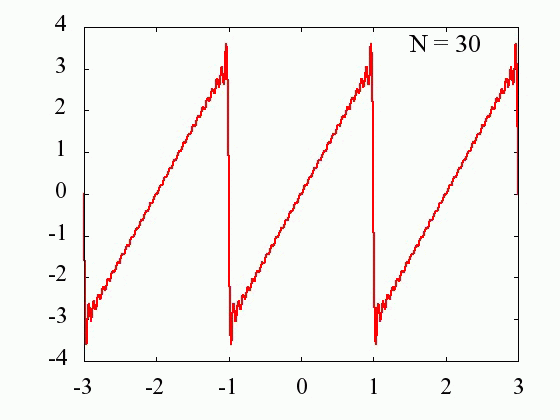
フーリエ級数１：f=x

物理現象を理解するうえで、非常に有効な道具にフーリエ級数展開があります。 フーリエ級数展開の有用性を理解するための準備として、解析的に求めた級数を用いて、元の関数を表現します。

元の関数　

区間[-π,π]で周期的な関数と定義します。

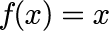
フーリエ級数展開

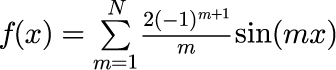
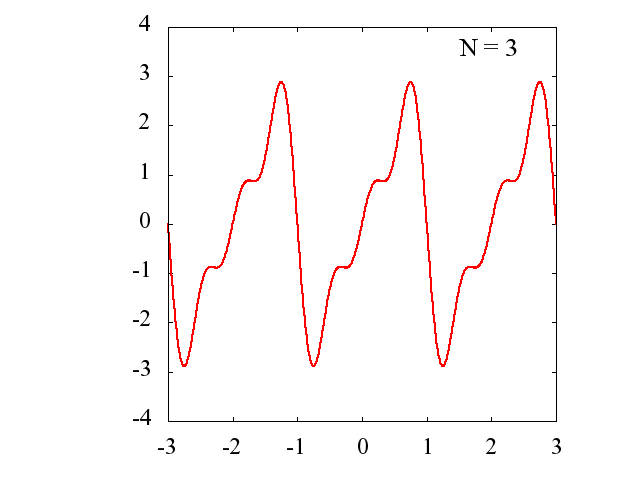
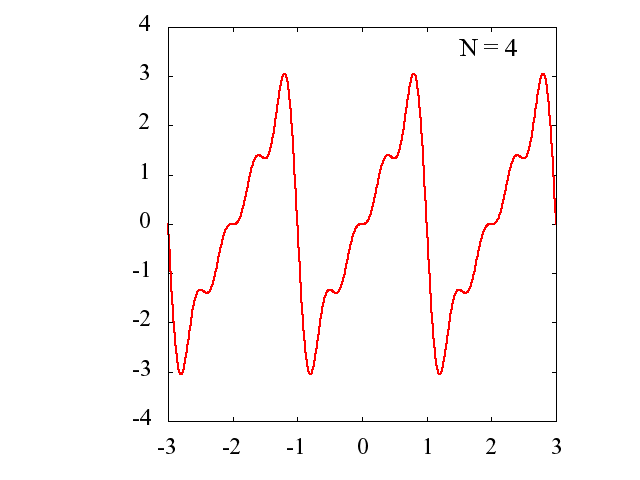
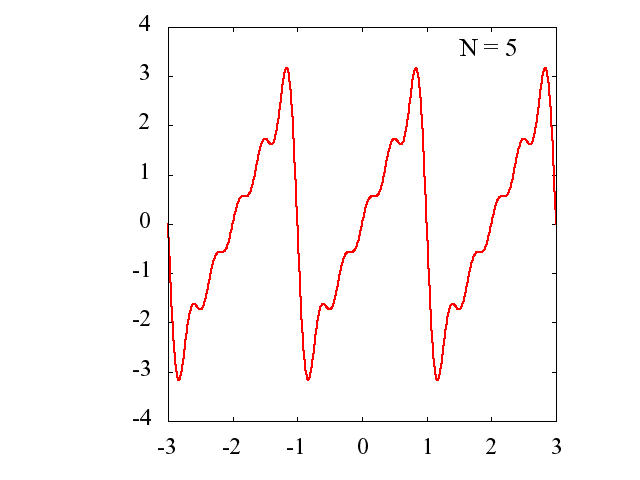
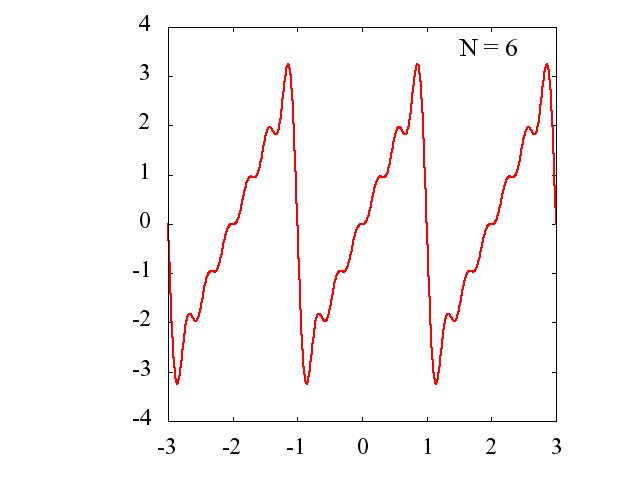
Nの値を多くするに従って、元の関数にどの様に近づいていくのかを見てみます。

横軸：x/π
縦軸：f(x)

C++ソース

Nごとに区間[-3π,3π]を描画します。

/*
フーリエ級数
f(x)=x [-PI,PI]
*/
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include <cstdio>
#include <iomanip>
#include <stdio.h>
#include <complex>
#include <direct.h>
using namespace std;

double PI = acos(-1.0);
double e = 2.7182818284590452354;
complex<double> I = complex<double>(0.0,1.0);
int xN =1000;
int N = 10;
int T = 3;
string folder = "1", ff="", fg="";  //保存フォルダ名
ostringstream fname;
double phi(double x, int n);

int main(){
 _mkdir(folder.c_str());
  for( N=1; N<=1000; N++){
    ostringstream fname_Psi;
    fname_Psi <<  folder   + "/" << N << ".data";//出力ファイル名
    string f_Psi = fname_Psi.str();
    ofstream fout_Psi;
    fout_Psi.open(f_Psi.c_str());

    for(int j=0; j<=xN; j++){
      double x = (- PI + 2.0 * PI * double(j)/double(xN))*T;
      double F=0.0;
      for(int i=1; i<=N; i++){
        F += phi(x, i);
      }
      fout_Psi << x/PI << " " << F << endl;
    }
  }
  return 0;
}

double phi(double x, int n){
  return pow(-1.0,n+1) * 2.0 * sin(double(n)*x) /double(n);
}

gnuplot テンプレート

データからjpgファイルを出力します

set terminal jpeg  enhanced font "Times" 20 size 560, 420
set tics font 'Times,18'
set rmargin 3
set lmargin 6
set nokey
set yr[-4:4]

if (exist("n")==0 || n<0) n=1 #変数の初期化

file0(n) = sprintf("1/%d.data",n) #入力ファイル名
outfile(n) = sprintf("1-/%d.jpg",n+10000)  #出力ファイル名
title(n) = sprintf("N = %d",n)  #タイトル名

unset label 
set label title(n)  font 'Times,20'  at 1.5 , 3.5 

set output outfile(n)
plot file0(n) u 1:2 w l lw 2 

if (n<1000)  n=n+1; reread

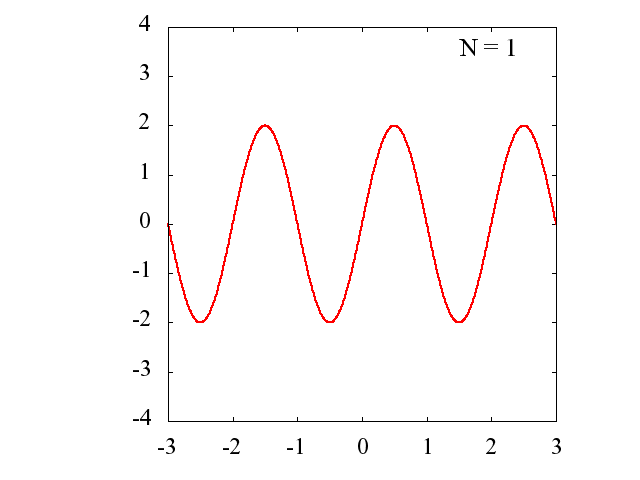
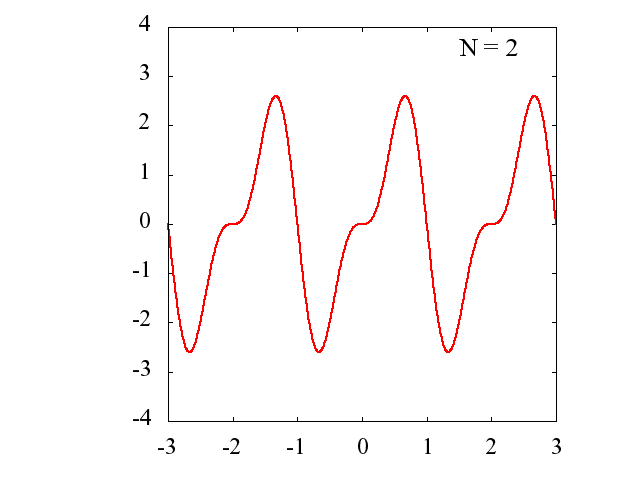
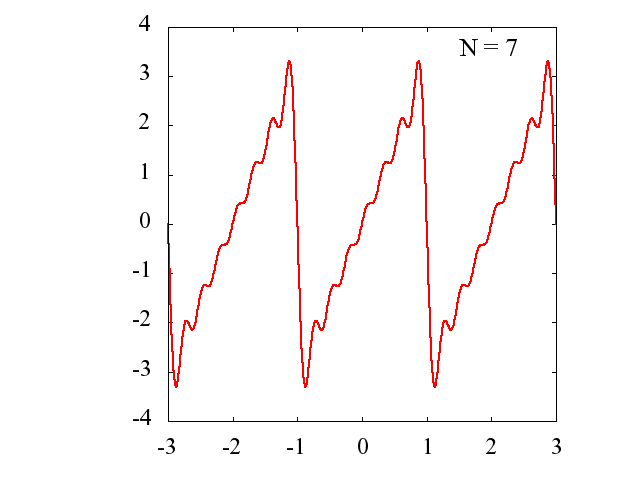
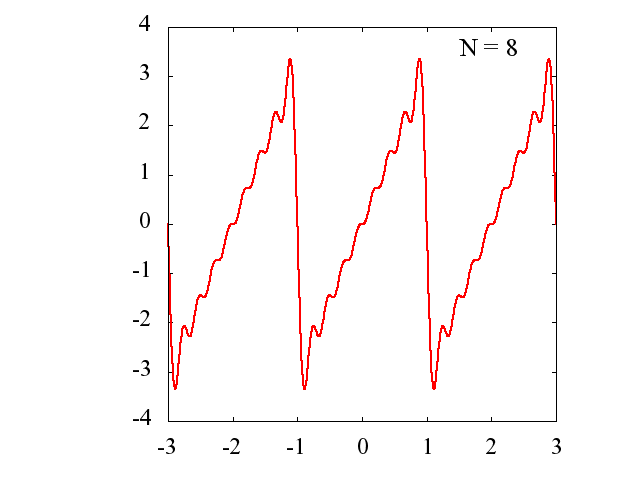
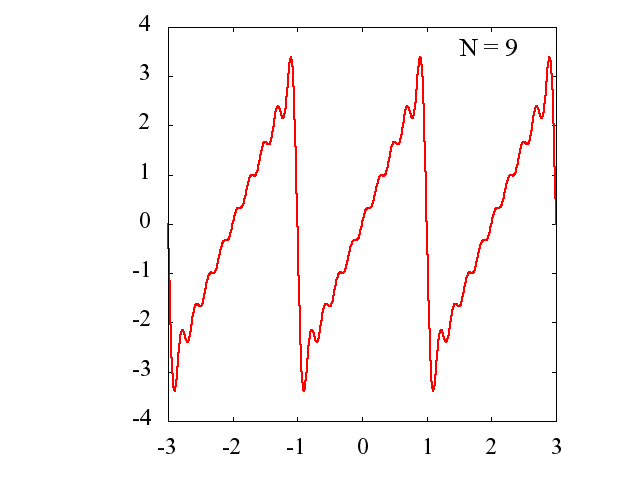
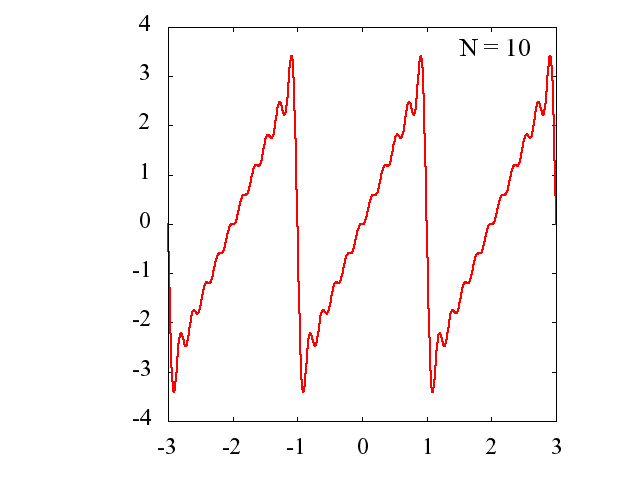
gif アニメーション