シュレディンガー方程式に従う粒子の時間発展
無限に深い２次元井戸型ポテンシャル２
文責：遠藤 理平 （2010年10月13日）
カテゴリ：仮想物理実験室(325)
シュレディンガー方程式に従う粒子の時間発展３：無限に深い２次元井戸型ポテンシャルの時間発展では、 波数空間におけるガウス分布の中心(k_0)が０の場合の時間発展を行いました。 本節では、k_0 が有限の場合のシミュレーションを行います。これまでと同様一辺が L=10[nm] の２次元井戸型ポテンシャルを想定します。
(k_0x, k_0y) = (10,0) の場合の波数空間におけるガウス分布
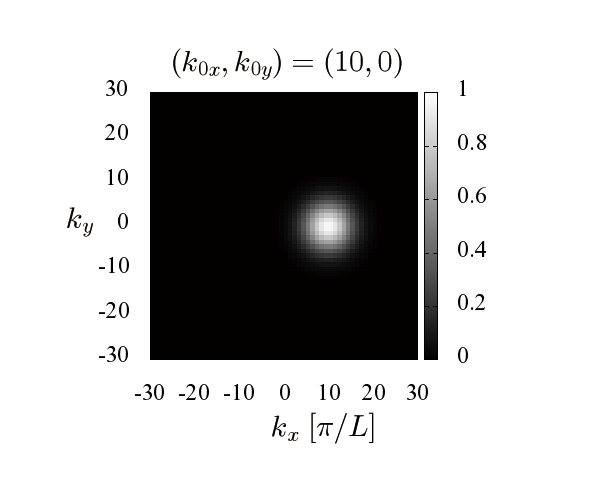
>(k_0x, k_0y) = (10,0) の場合の時間発展
縦軸：実空間 x 0と10[nm]がポテンシャル障壁
横軸: 実空間 y 0と10[nm]がポテンシャル障壁
色：黒色→存在確率0
パルスの中心座標：r_0 = (L/2,L/2)
時間間隔： 10^{-15}[s]
考察
考察については、また後日あらためて行ないます。
VisualC++ ＋ gnuplotによるアニメーション
後日あらためて公開します。
