【波動論３】
ステップ関数のフーリエ級数展開

ステップ関数は次のような関数で定義されます。

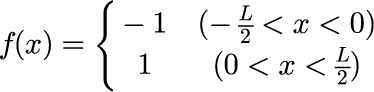
上記のステップ関数をフーリエ級数で表すと次のようになります。

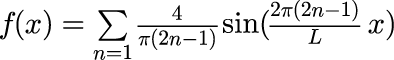
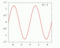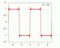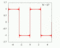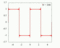
L=5 の場合のステップ関数

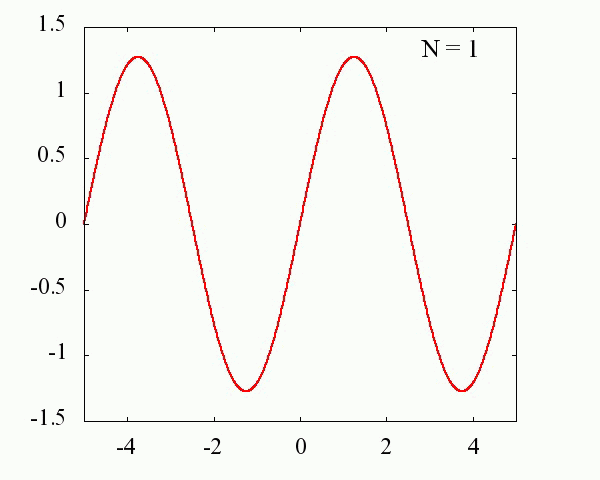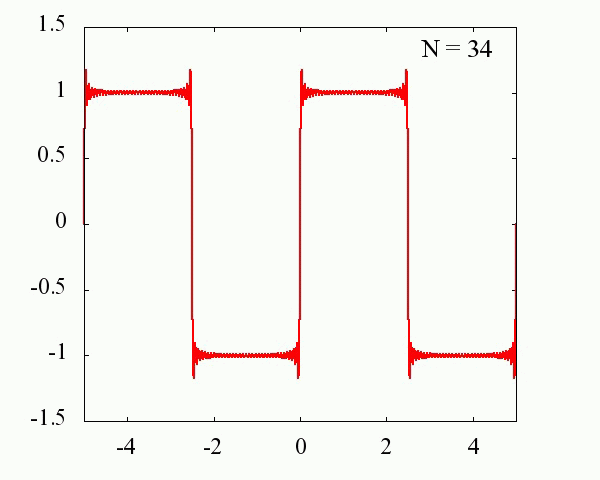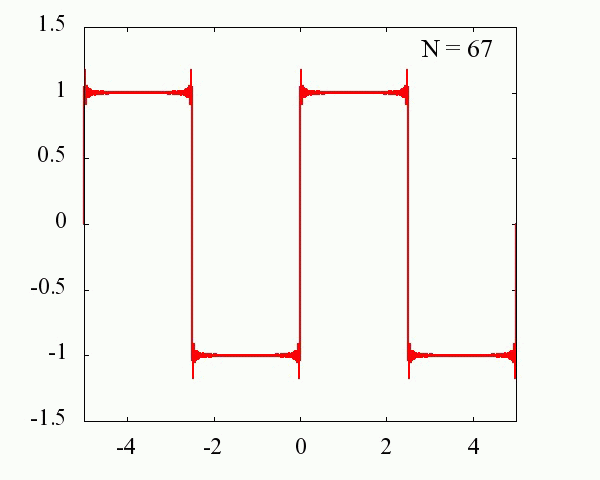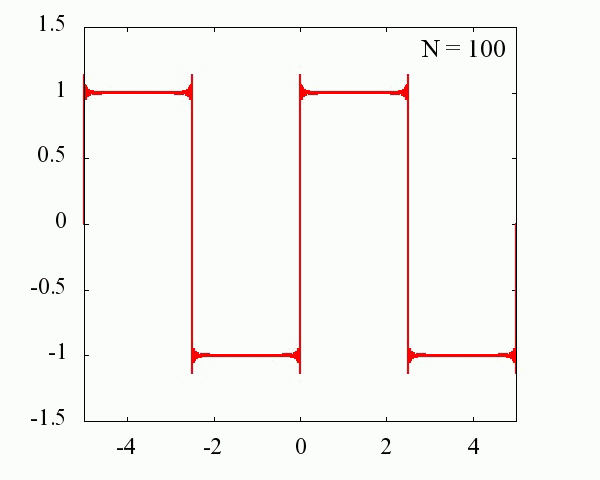
Nが大きくなるにつれ、元の関数に近づいていくことが分かります。

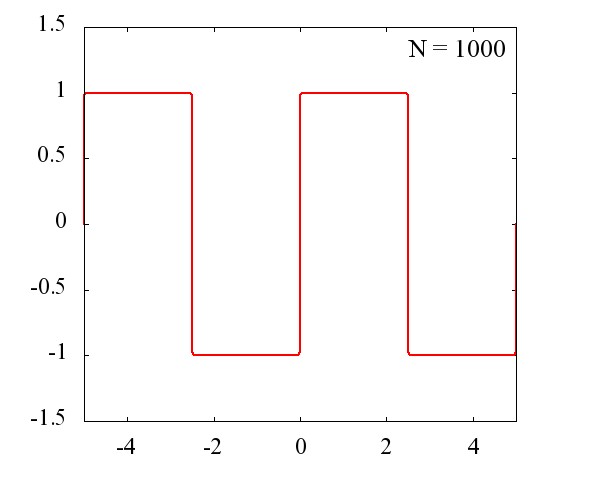
N=1000 ではほとんど再現出来ているように見えます。

C++ プログラム

各Nごとに、xの区間[-L,L]の値を書き出すプログラムです。
1.data ～ 1000.data までのファイルがフォルダ名「1」の中に書き出されます。

/*
フーリエ級数
ステップ関数 [-L/2,L/2]
*/
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include <cstdio>
#include <iomanip>
#include <stdio.h>
#include <complex>
#include <direct.h>
using namespace std;

double PI = acos(-1.0);
double e = 2.7182818284590452354;
complex<double> I = complex<double>(0.0,1.0);
double L = 5.0;
int xN =1000;
int N = 1000;
int T = 2;
string folder = "1", ff="", fg="";  //保存フォルダ名
ostringstream fname;
double phi(double x, int n);

int main(){
 _mkdir(folder.c_str());
  for(int i=1; i<=N; i++){
    cout << i << endl;
    char str[100];
    sprintf_s( str ,"%d.data",i);
    string st = folder + "/" + string(str);
    ofstream fout_f;
    fout_f.open(st.c_str());
    for(int j=0; j<=xN; j++){
      double F=0.0;
      double x = (- L/2.0 + L * double(j)/double(xN))*T;
      for(int k=1; k<=i; k++){
        F += phi(x, k);
      }
      fout_f << x << " " << F << endl;
    }
    fout_f.close();
  }
  return 0;
}

double phi(double x, int n){
  return  4.0/(double(2*n-1)*PI) * sin(2.0*PI*double(2*n-1)/L*x);
}

gnuplot テンプレート

1.data ～ 1000.data までのファイルをgnuplot を利用して、それぞれ jpg ファイルに書き出し連番ファイルを生成します。 図はフォルダ名「1-」の中に書き出されます。予めフォルダ名「-1」のフォルダを用意しておきます。

set terminal jpeg  enhanced font "Times" 20 size 600, 480
set tics font 'Times,18'
set rmargin 3
set lmargin 3
set nokey
set xr[-5:5]
set yr[-1.5:1.5]

if (exist("n")==0 || n<0) n=1 #変数の初期化

file0(n) = sprintf("1/%d.data",n) #入力ファイル名
outfile(n) = sprintf("1-/%d.jpg",n+10000)  #出力ファイル名
title(n) = sprintf("N = %d",n)  #タイトル名

unset label 
set label title(n)  font 'Times,20'  at 2.8 , 1.3 

set output outfile(n)
plot file0(n) u 1:2 w l lw 2 

if (n<1000)  n=n+1; reread

書き出された連番jpgファイルから、動画を作成します。