波動論
太鼓の振動の固有振動（第１種ベッセル関数）

ベッセル関数を用いて、太鼓の振動（円形膜の振動）の固有状態を描画します。

膜振動の微分方程式と固有解

面密度ρ
張力T
変位 u(x,y)
とした場合、微小膜片の運動方程式から、微分方程式が得られます。

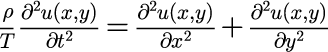
太鼓の場合に適応する場合、上記運動方程式を２次元極座標であらわし、変数分離で解くことができます。

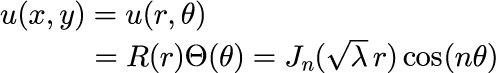
J_n(x) は第一種ベッセル関数と呼ばれるよく知られた特殊関数の一つです。 λ は変数分離時に現れるの定数で、太鼓のふちで変位が 0 となる条件から、決めることができます。

太鼓の振動の固有振動

境界条件 J_n(x) = 0 を満たす x の値は無限にあります。
xの小さいほうから順番に m=0,1,2... とします。

n=0 の場合

太鼓の中心を叩いた場合は、角度依存がないので n=0 だけで記述することができます。

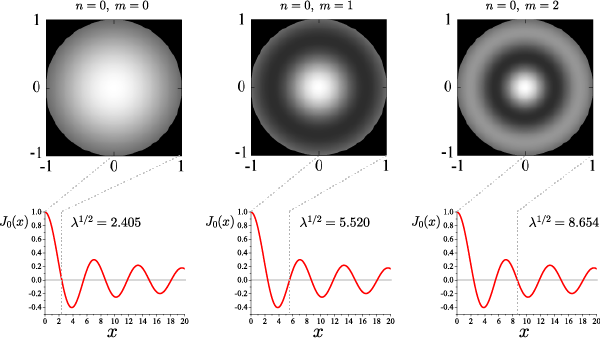
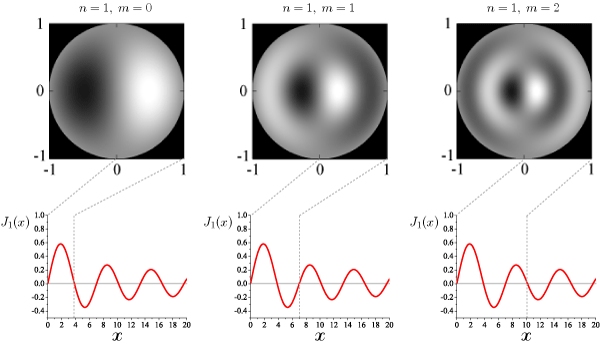
n=1の場合

中心以外を叩いた場合、n=0 以外の固有振動も励起されます。

gnuplot テンプレート

set pm3d
set pm3d map
set ticslevel 0
set size square
set nokey
set rmargin 4
set tics font 'Times,18'

#set term postscript eps enhanced color 'Times-Roman' 24
set terminal jpeg  enhanced font "Times" 20 size 600, 480

set xr[-1:1]
set yr[-1:1]
set parametric
set urange [0:1]
set vrange [0:2*pi]
set isosample 1000,1000

fx(u,v)=u*cos(v)
fy(u,v)=u*sin(v)
J0(u,v)=besj0(u)
J1(u,v)=besj1(u)*cos(v)

set cbrange[-0.7:1.0]
set palette defined ( -0.7 "black" , 1.0 "white")
lamda=2.405
set output 'J0_0.jpg'
splot fx(u,v), fy(u,v), J0(lamda*u,v) with pm3d
lamda=5.520
set output 'J0_1.jpg'
splot fx(u,v), fy(u,v), J0(lamda*u,v) with pm3d
lamda=8.654
set output 'J0_2.jpg'
splot fx(u,v), fy(u,v), J0(lamda*u,v) with pm3d

set cbrange[-0.7:0.55]
set palette defined ( -0.7 "black" , 0.55 "white")
lamda=3.832
set output 'J1_0.jpg'
splot fx(u,v), fy(u,v), J1(lamda*u,v) with pm3d
lamda=7.016
set output 'J1_1.jpg'
splot fx(u,v), fy(u,v), J1(lamda*u,v) with pm3d
lamda=10.174
set output 'J1_2.jpg'
splot fx(u,v), fy(u,v), J1(lamda*u,v) with pm3d

exit