【OpenGL入門】
直方体を回転させよう！

コンピュータシミュレーション講座では、 コンピュータ上での物理シミュレーションが目的ですが、 その手前としてOpenGLを用いた描画の練習を沢山行います。 本稿では、直方体を自由に描画するための練習を行ないます。

直方体を回転させよう！

直方体を描画する際の自由度は、

各辺の長さ（３つ）、
重心の位置（３つ）、 回転軸ベクトル（３つ）、
回転角度（１つ）

です。OpenGLで描画する際にはそれに色を指定します。
座標軸は上がz座標, 右がx座標、奥がy座標の右手系です。

回転軸ベクトル＝(0,0,1)

回転軸ベクトル＝(1,0,0)

回転軸ベクトル＝(0,1,0)

回転軸ベクトル＝(1,0,1)

回転軸ベクトル＝(1,1,0)

回転軸ベクトル＝(0,1,1)

回転軸ベクトル＝(1,1,1)

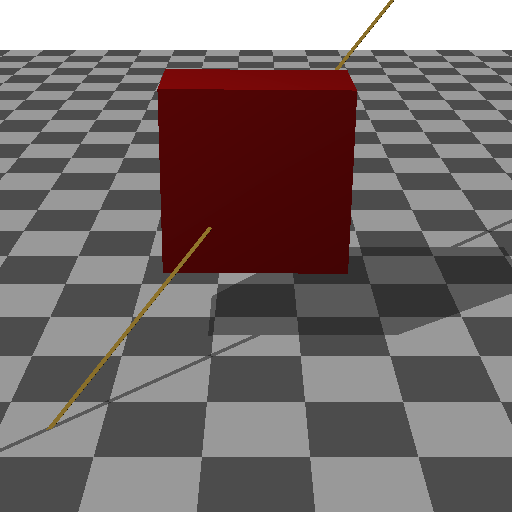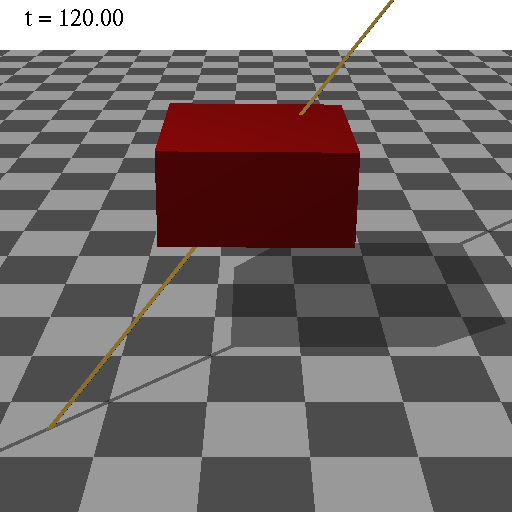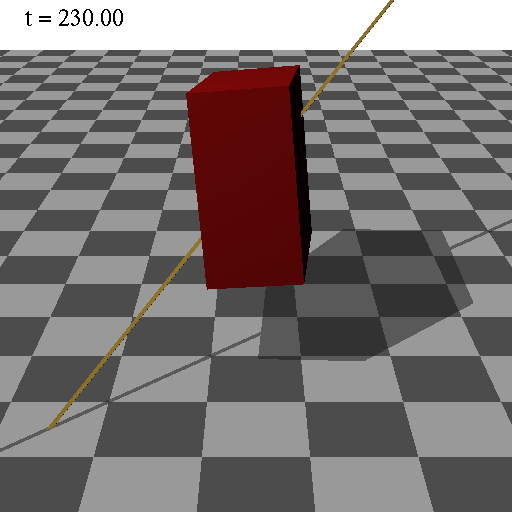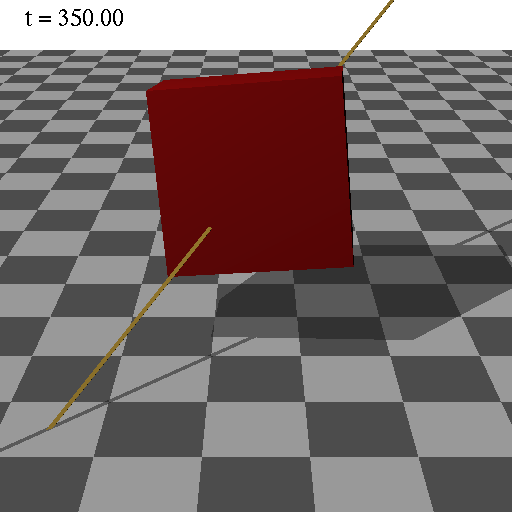
OpenGLのプログラム

直方体描画関数のプロトタイプ

直方体を描画する際に、回転なしと回転ありとの２つの関数をオーバーロードで表現しています。

 
drowCuboid(double a, double b, double c,     // x軸方向の幅, y軸方向の幅, z軸方向の幅,
           double x, double y, double z,     // 中心のx座標, 中心のy座標, 中心のz座標, 
           MaterialStruct color);            // 色
drowCuboid(double a, double b, double c,     // x軸方向の幅, y軸方向の幅, z軸方向の幅,
           double x, double y, double z,     // 中心のx座標, 中心のy座標, 中心のz座標, 
           MaterialStruct color,             // 色,
           double theta,                     // 回転角度, 
           double nx, double ny, double nz); // 回転軸x座標, 回転軸y座標, 回転軸z標

直方体描画関数

 
/////////////////////////////////////////////
// 直方体の描画
void drowCuboid(double a, double b, double c, 
                double x, double y, double z, 
                MaterialStruct color){
  GLdouble vertex[][3] = {
      { -a/2.0, -b/2.0, -c/2.0 },
      {  a/2.0, -b/2.0, -c/2.0 },
      {  a/2.0,  b/2.0, -c/2.0 },
      { -a/2.0,  b/2.0, -c/2.0 },
      { -a/2.0, -b/2.0,  c/2.0 },
      {  a/2.0, -b/2.0,  c/2.0 },
      {  a/2.0,  b/2.0,  c/2.0 },
      { -a/2.0,  b/2.0,  c/2.0 }
    };
  int face[][4] = {//面の定義
      { 3, 2, 1, 0 },
      { 1, 2, 6, 5 },
      { 4, 5, 6, 7 },
      { 0, 4, 7, 3 },
      { 0, 1, 5, 4 },
      { 2, 3, 7, 6 }
    };
  GLdouble normal[][3] = {//面の法線ベクトル
    { 0.0, 0.0, -1.0 },
    { 1.0, 0.0, 0.0 },
    { 0.0, 0.0, 1.0 },
    {-1.0, 0.0, 0.0 },
    { 0.0,-1.0, 0.0 },
    { 0.0, 1.0, 0.0 }
  };
    glPushMatrix();
      glMaterialfv(GL_FRONT, GL_AMBIENT, color.ambient);
      glMaterialfv(GL_FRONT, GL_DIFFUSE, color.diffuse);
      glMaterialfv(GL_FRONT, GL_SPECULAR, color.specular);
      glMaterialfv(GL_FRONT, GL_SHININESS, &color.shininess);
      glTranslated( x, y, z);//平行移動値の設定
      glBegin(GL_QUADS);
      for (int j = 0; j < 6; ++j) {
        glNormal3dv(normal[j]); //法線ベクトルの指定
        for (int i = 0; i < 4; ++i) {
          glVertex3dv(vertex[face[j][i]]);
        }
      }
      glEnd();
    glPopMatrix();
}
//回転を考慮した立方体の描画
void drowCuboid(double a, double b, double c, 
                double x, double y, double z, 
                MaterialStruct color, 
                double theta, 
                double nx, double ny, double nz){
  double nn =sqrt(pow(nx,2)+pow(ny,2)+pow(nz,2));
  if(nn>0.0){
    nx = nx/nn;
    ny = ny/nn;
    nz = nz/nn;
  }
  glPushMatrix();
    glTranslated( x, y, z);//平行移動値の設定
    glPushMatrix();
      if(theta!=0 && nn>0.0) glRotated( theta , nx , ny, nz);
      drowCuboid(a, b, c, 0, 0, 0, color);
    glPopMatrix();
  glPopMatrix();
}

上記プログラムの例

 
  th++; //角度を描画ごとに１づつ増加させる
  drowCuboid(20.0, 10.0, 20.0, //x軸方向の幅, y軸方向の幅, z軸方向の幅,
             0.0, 0.0, 20.0,   //中心のx座標, 中心のy座標, 中心のz座標,
             ms_ruby,          //色,
             th,               //回転角度,
             0.0, 0.0, 1.0);   //回転軸x座標, 回転軸y座標, 回転軸z標
}