擬似乱数生成器：メルセンヌ・ツイスタの使い方

擬似乱数生成器とは？

コンピュータを用いて、確率過程が入るシミュレーションを行う場合、決められた範囲の数がランダムに出現する乱数が必須となります。 しかしながら、コンピュータをもちいて乱数を発生させる場合、決定論的な計算から一見ランダムなものを擬似的に生成することしかできません。つまり、乱数の良さがシミュレーションの結果を左右することになります。

コンピュータなどを用いて生成する乱数は擬似乱数と呼ばれます。 また、擬似乱数を生成する器械は擬似乱数生成器、それに用いられているアルゴリズムは擬似乱数生成法と呼ばれます。 よい擬似乱数を得るためには、当然よい擬似乱数生成法が必要となります。 コンピュータを用いて擬似乱数を生成する場合、よい乱数の条件は「周期が長い」ことがあげられます。 コンピュータ特有の有限桁精度のため、生成する擬似乱数に周期性が存在します。 もし、擬似乱数を用いる回数がその周期よりも長ければ、シミュレーション結果に重大な影響を与える場合があります。

擬似乱数生成器：メルセンヌ・ツイスタ

周期が 2^19937-1 である擬似乱数生成器「メルセンヌ・ツイスタ」があります。 この生成器は松本眞氏と西村拓士氏によって開発され、よく利用されています。 2^19937-1は素数のひとつで「メルセンヌ数」と呼ばれ、この生成器の語源となっています。

メルセンヌ・ツイスタは、BSDライセンスで公開されているので、ほんの少し改造してこちらで紹介いたします。

C言語ソース：メルセンヌ・ツイスタ（mt19937ar.h）

 
namespace mt{
/* 
   A C-program for MT19937, with initialization improved 2002/1/26.
   Coded by Takuji Nishimura and Makoto Matsumoto.

   Before using, initialize the state by using init_genrand(seed)  
   or init_by_array(init_key, key_length).

   Copyright (C) 1997 - 2002, Makoto Matsumoto and Takuji Nishimura,
   All rights reserved.
   Copyright (C) 2005, Mutsuo Saito
   All rights reserved.

   Redistribution and use in source and binary forms, with or without
   modification, are permitted provided that the following conditions
   are met:

     1. Redistributions of source code must retain the above copyright
        notice, this list of conditions and the following disclaimer.

     2. Redistributions in binary form must reproduce the above copyright
        notice, this list of conditions and the following disclaimer in the
        documentation and/or other materials provided with the distribution.

     3. The names of its contributors may not be used to endorse or promote 
        products derived from this software without specific prior written 
        permission.

   THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS
   "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT
   LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR
   A PARTICULAR PURPOSE ARE DISCLAIMED.  IN NO EVENT SHALL THE COPYRIGHT OWNER OR
   CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL,
   EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO,
   PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR
   PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF
   LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING
   NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS
   SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.


   Any feedback is very welcome.
   http://www.math.sci.hiroshima-u.ac.jp/~m-mat/MT/emt.html
   email: m-mat @ math.sci.hiroshima-u.ac.jp (remove space)
*/

/* initializes mt[N] with a seed */
void init_genrand(unsigned long s);

/* initialize by an array with array-length */
/* init_key is the array for initializing keys */
/* key_length is its length */
/* slight change for C++, 2004/2/26 */
void init_by_array(unsigned long init_key[], int key_length);

/* generates a random number on [0,0xffffffff]-interval */
unsigned long genrand_int32(void);

/* generates a random number on [0,0x7fffffff]-interval */
long genrand_int31(void);

/* These real versions are due to Isaku Wada, 2002/01/09 added */
/* generates a random number on [0,1]-real-interval */
double genrand_real1(void);

/* generates a random number on [0,1)-real-interval */
double genrand_real2(void);

/* generates a random number on (0,1)-real-interval */
double genrand_real3(void);

/* generates a random number on [0,1) with 53-bit resolution*/
double genrand_res53(void);


#include <stdio.h>

/* Period parameters */  
const int N=624;
const int M=397;
#define MATRIX_A 0x9908b0dfUL   /* constant vector a */
#define UPPER_MASK 0x80000000UL /* most significant w-r bits */
#define LOWER_MASK 0x7fffffffUL /* least significant r bits */

static unsigned long mt[N]; /* the array for the state vector  */
static int mti=N+1; /* mti==N+1 means mt[N] is not initialized */

/* initializes mt[N] with a seed */
void init_genrand(unsigned long s)
{
    mt[0]= s & 0xffffffffUL;
    for (mti=1; mti<N; mti++) {
        mt[mti] = 
	    (1812433253UL * (mt[mti-1] ^ (mt[mti-1] >> 30)) + mti); 
        /* See Knuth TAOCP Vol2. 3rd Ed. P.106 for multiplier. */
        /* In the previous versions, MSBs of the seed affect   */
        /* only MSBs of the array mt[].                        */
        /* 2002/01/09 modified by Makoto Matsumoto             */
        mt[mti] &= 0xffffffffUL;
        /* for >32 bit machines */
    }
}

/* initialize by an array with array-length */
/* init_key is the array for initializing keys */
/* key_length is its length */
/* slight change for C++, 2004/2/26 */
void init_by_array(unsigned long init_key[], int key_length)
{
    int i, j, k;
    init_genrand(19650218UL);
    i=1; j=0;
    k = (N>key_length ? N : key_length);
    for (; k; k--) {
        mt[i] = (mt[i] ^ ((mt[i-1] ^ (mt[i-1] >> 30)) * 1664525UL))
          + init_key[j] + j; /* non linear */
        mt[i] &= 0xffffffffUL; /* for WORDSIZE > 32 machines */
        i++; j++;
        if (i>=N) { mt[0] = mt[N-1]; i=1; }
        if (j>=key_length) j=0;
    }
    for (k=N-1; k; k--) {
        mt[i] = (mt[i] ^ ((mt[i-1] ^ (mt[i-1] >> 30)) * 1566083941UL))
          - i; /* non linear */
        mt[i] &= 0xffffffffUL; /* for WORDSIZE > 32 machines */
        i++;
        if (i>=N) { mt[0] = mt[N-1]; i=1; }
    }

    mt[0] = 0x80000000UL; /* MSB is 1; assuring non-zero initial array */ 
}

/* generates a random number on [0,0xffffffff]-interval */
unsigned long genrand_int32(void)
{
    unsigned long y;
    static unsigned long mag01[2]={0x0UL, MATRIX_A};
    /* mag01[x] = x * MATRIX_A  for x=0,1 */

    if (mti >= N) { /* generate N words at one time */
        int kk;

        if (mti == N+1)   /* if init_genrand() has not been called, */
            init_genrand(5489UL); /* a default initial seed is used */

        for (kk=0;kk<N-M;kk++) {
            y = (mt[kk]&UPPER_MASK)|(mt[kk+1]&LOWER_MASK);
            mt[kk] = mt[kk+M] ^ (y >> 1) ^ mag01[y & 0x1UL];
        }
        for (;kk<N-1;kk++) {
            y = (mt[kk]&UPPER_MASK)|(mt[kk+1]&LOWER_MASK);
            mt[kk] = mt[kk+(M-N)] ^ (y >> 1) ^ mag01[y & 0x1UL];
        }
        y = (mt[N-1]&UPPER_MASK)|(mt[0]&LOWER_MASK);
        mt[N-1] = mt[M-1] ^ (y >> 1) ^ mag01[y & 0x1UL];

        mti = 0;
    }
  
    y = mt[mti++];

    /* Tempering */
    y ^= (y >> 11);
    y ^= (y << 7) & 0x9d2c5680UL;
    y ^= (y << 15) & 0xefc60000UL;
    y ^= (y >> 18);

    return y;
}

/* generates a random number on [0,0x7fffffff]-interval */
long genrand_int31(void)
{
    return (long)(genrand_int32()>>1);
}

/* generates a random number on [0,1]-real-interval */
double genrand_real1(void)
{
    return genrand_int32()*(1.0/4294967295.0); 
    /* divided by 2^32-1 */ 
}

/* generates a random number on [0,1)-real-interval */
double genrand_real2(void)
{
    return genrand_int32()*(1.0/4294967296.0); 
    /* divided by 2^32 */
}

/* generates a random number on (0,1)-real-interval */
double genrand_real3(void)
{
    return (((double)genrand_int32()) + 0.5)*(1.0/4294967296.0); 
    /* divided by 2^32 */
}

/* generates a random number on [0,1) with 53-bit resolution*/
double genrand_res53(void) 
{ 
    unsigned long a=genrand_int32()>>5, b=genrand_int32()>>6; 
    return(a*67108864.0+b)*(1.0/9007199254740992.0); 
} 
/* These real versions are due to Isaku Wada, 2002/01/09 added */
}

【改造点】

１．名前衝突を避けるために namespace 「mt」を設定
２．#define で定義されている変数を const に変更変数

具体的には、

 
#define N 624;
#define M 397;

を

 
const int N=624;
const int M=397;

としました。

メルセンヌ・ツイスタの使いかた

擬似乱数をもちいて、さいころの「１」が出る確率計算するプログラム

 
//////////////////////////////////////////////////////////////////////////
// メルセンヌ・ツイスタの使いかた
//////////////////////////////////////////////////////////////////////////
#include <math.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <time.h>
#include <mt19937ar.h> //メルセンヌ・ツイスタ
using namespace std;
ofstream file1( "mt.data" );
const int N = 1000000; //回数

//////////////////////////////////////////////////////////////////////////////////
// メイン関数
//////////////////////////////////////////////////////////////////////////////////
int main(){
  mt::init_genrand((unsigned)time(NULL));
  int c = 0;
  for(int i=1; i<=N; i++){
    //mt::genrand_real1() は [0,1] でランダム
    if(mt::genrand_real1()*6.0 < 1.0) c++;
    if(i%10==0) file1 << i << " " << double(c)/double(i)  << endl;
  }
  return 0;
}

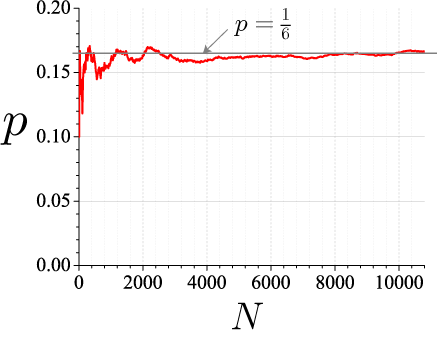
計算結果

横軸：試行回数
縦軸：１の目が出た確率（１の目が出た回数／試行回数）

課題メモ

１．C言語の rand 関数との性能の比較を行う

目次

第１章　序章

• １－１．Duffing振子のカオス的運動のシミュレーション
• １－２．Duffing振子の位相空間上でのカオス的運動のアニメーション
• １－３．Duffing振子の位相空間上のストレンジ・アトラクタに対するフラクタル次元
• ２－１．DLAによる樹木状クラスタのシミュレーション
• ２－２．DLAによる樹木状クラスタのフラクタル次元

第２章　対称ポテンシャルによる量子散乱

ゴール：水素原子のクリプトン原子による散乱に対する散乱断面積の計算

• ・ヌメロフ法による常微分方程式の解法
• ・球ベッセル関数
• ・ルジャンドル多項式
• ・位相シフト→断面積を計算するアルゴリズム

その他

• ・擬似乱数生成器：メルセンヌ・ツイスタの使い方
• ・ランダムウォークによる擬似乱数の比較：C言語rand関数とメルセンヌ・ツイスタ(mt19937ar)