ランダムウォークによる擬似乱数の比較 ：C言語rand関数とメルセンヌ・ツイスタ(mt19937ar)

ランダムウォークとは、各時間ステップごとに与えられた空間内を与えられた確率で各方向に移動する運動のことで、 日本語では酔歩などと呼ばれます。 「与えられた確率で移動する」とは、各時間ステップによる移動はこれまでの過去の履歴に依存せず、独立であることを意味します。 「各時間ステップ（離散時間ステップ）」による移動が「独立」である過程はベルヌーイ過程と呼ばれます。 ランダムウォークは単純なモデルですが、巨視的には確率過程とみなせる場合に非常に有用で様々な分野で積極的に利用されています。

擬似乱数を用いてランダムウォークを行います。 擬似乱数には、良し悪しがあることが知られています。 C言語で乱数を発生させる場合、最も簡単なのが組込み関数 rand() を利用することです。 しかしながら、rand() 関数による乱数の質は高くないことが知られています。

本稿では１次元ランダムウォークに対して、

１．rand()を利用
２．メルセンヌ・ツイスタを利用（【参考】擬似乱数生成器：メルセンヌ・ツイスタの使い方）
３．理論値

の場合について比較することで、擬似乱数の良し悪しを確認します。

１次元ランダムウォークのモデル

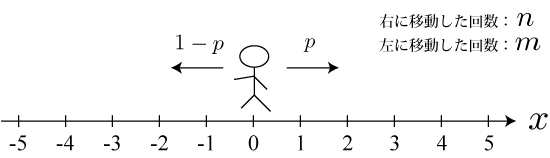
１次元直線上を移動するランダムウォークを考えます。
運動を終了する時間ステップを N 、
運動を終了したとき（Nステップ後）の位置 x 、
右に移動した回数を n 、左に移動した回数を m 、
各時間ステップで右に移動する確率を p とすると、左に移動する確率波は 1-p となります。

右に移動した回数が n となる確率は二項分布に従うので、次のように書くことができます。

(1)

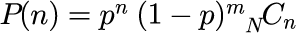
「C」は組み合わせ数を計算するコンビネーションです。
変数 n と m と x, N は独立ではありません。

(2)

の関係性があるので、n と m は x と N を用いて次のように表すことができます。

(3)

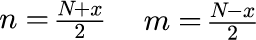
式(3)を式(1)に代入することで、N 時間ステップ後の位置が x となる確率が計算できました。

(4)

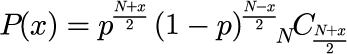
数値計算：１次元ランダムウォーク

右と左に移動する確率（p=1/2）が同じ場合を考えることにします。
C言語の組込み関数 rand() とメルセンヌ・ツイスタの関数 genrand_real1() を用いての結果をファイル名「distribution.data」に書き出します。

プログラムソース：確率分布P(x)の計算

 
//////////////////////////////////////////////////////////////////////////
// メルセンヌ・ツイスタとrand関数の比較（ランダムウォーク）.cpp
// 乱数生成器の比較（cのrand関数とmt）
//////////////////////////////////////////////////////////////////////////
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include <cstdio>
#include <iomanip>
#include <stdio.h>
#include "mt19937ar.h" //メルセンヌ・ツイスタ
using namespace std;

const int dimension = 1; //次元
const int N     = 1000000; //ランダム・ウォーカーの人数
const int s_end = 1000000; //ステップ数
const int center = s_end/20;
int distribution_cr[2*center+1] = {0}; //原点を distribution_cr[center]とする
int distribution_mt[2*center+1] = {0}; //原点を distribution_mt[center]とする

ofstream file1( "distribution.data" );

int main(){
  mt::init_genrand((unsigned)time(NULL));
  srand((unsigned)time(NULL));

  for(int i=0; i<N; i++){
    int p_cr[N] ={0};
    int p_mt[N] ={0};

    for(int s=1; s<=s_end; s++){
      if(double(rand())/double(RAND_MAX)<0.5) p_cr[i]++;
      else p_cr[i]--;
      if(mt::genrand_real1()<0.5) p_mt[i]++;
      else p_mt[i]--;
    }
    distribution_cr[center+p_cr[i]]++;
    distribution_mt[center+p_mt[i]]++;
    if(i%1000==0) cout << i << " " ;
  }
  for(int i=0; i<=2*center-2; i=i+2){
    file1 << i-center << " " << double(distribution_cr[i])/double(N) << " " << double(distribution_mt[i])/double(N) << endl;
  }
}

上記プログラムを実行すると計算結果が「distribution.data」に書き出されます。

【注意】乱数の範囲
■rand()：[0:RAND_MAX] （0からRAND_MAX の間）
■genrand_real1()：[0:1]

プログラムソース：確率分布P(x)の理論値の計算

 
//////////////////////////////////////////////////////////////////////////
// ランダムウォークの厳密解
//////////////////////////////////////////////////////////////////////////
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include <cstdio>
#include <iomanip>
#include <stdio.h>
using namespace std;

const int dimension = 1; //次元
const int s_end = 1000000; //ステップ数
const int center = s_end/20;
int distribution_cr[2*center+1] = {0};
ofstream file1( "distribution_exact.data" );

double distribution(int x, int N); // nCm の計算

int main(){
  for(int s=-5000; s<=5000; s+=10){
    long int nf;
    file1 << s << " " << distribution(s,s_end) <<endl;
    cout << s << " " << distribution(s,s_end) <<endl;
  }
  //cin.get();
}
double distribution(int x, int N){
  int m;
  if(x>=0) m = (N-x)/2;
  else     m = (N+x)/2;
  double P = 1.0;
  int j=0;
  for(int i=1; i<=m; i++){
    P *= double(N-i+1)/double(m-i+1);
    while(P>1.0 && j<N){
      P/=2.0;
      j++;
    }
  }
  P/=pow(2.0,N-j);
  return P;
}

計算結果：ランダムウォークの確率分布

縦軸：確率 P(x)
横軸：位置 x

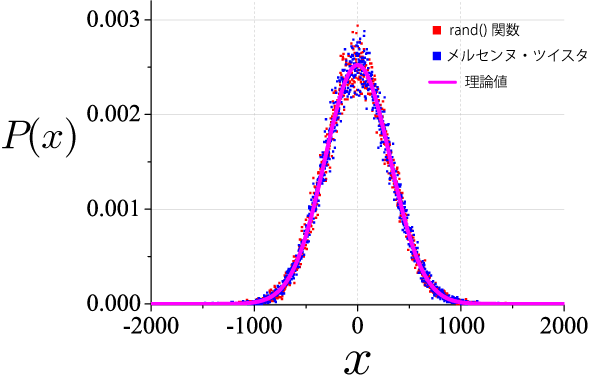
この結果だけは、擬似乱数の良し悪しは判断できないので、 統計量である平均 E と分散 V を計算し理論値と比較します。

ランダムウォークの平均と分散

右へ移動する確率 p 、ステップ数 N の場合、平均 E と 分散 V の理論値は次のようになります。

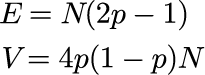
「メルセンヌ・ツイスタとrand関数の比較（ランダムウォーク）.cpp」で出力したファイル「distribution.data」を読み込んで、 平均 E と 分散 V を計算し、理論値と比較して擬似乱数の良し悪しを判定します。

プログラムソース：ランダムウォークの平均と分散

 
//////////////////////////////////////////////////////////////////////////
// ランダムウォークの平均と分散.cpp
//////////////////////////////////////////////////////////////////////////
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include <cstdio>
#include <iomanip>
#include <stdio.h>
using namespace std;

const int s_end = 100000; //ステップ数
const int center = s_end/10;
int distribution_cr[2*center+1] = {0}; //原点を distribution_cr[center]とする
int distribution_mt[2*center+1] = {0}; //原点を distribution_mt[center]とする

int main(){
  ifstream fin_position;
  fin_position.open("distribution_1.data");
  
  double ave_cr=0, ave_mt=0;
  double var_cr=0, var_mt=0;
  while(!fin_position.eof()){
    int ii;
    double p1, p2;
    fin_position >> ii; 
    fin_position >> p1; 
    fin_position >> p2; 
    if(ii+center<0) break;
    ave_cr += ii * p1;
    ave_mt += ii * p2;
    var_cr += ii*ii * p1;
    var_mt += ii*ii * p2;
    distribution_cr[ii+center]=p1; //原点を distribution_cr[center]とする
    distribution_mt[ii+center]=p2;
  }
  fin_position.close();
  cout <<"           rand()       MT       理論値"   << endl;
  cout <<"平均 E    "<< ave_cr << "    "  << ave_mt << "     " << 0    << endl;
  cout <<"分散 V     "<< var_cr << "    " << var_mt << "     " << s_end <<endl;
  cin.get();
}

計算結果：ランダムウォークの平均と分散

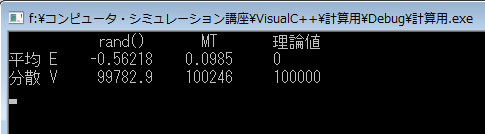
ステップ数：100000
試行回数： 100000
で実行した場合、平均値はMTの方がrandよりも理論値に近いが、分散は同程度でした。 試行回数を増やすことでより顕著な違いが出るのかもしれません。

課題メモ

１．試行回数を1000000回にして、擬似乱数の違いを調べる

目次

第１章　序章

• １－１．Duffing振子のカオス的運動のシミュレーション
• １－２．Duffing振子の位相空間上でのカオス的運動のアニメーション
• １－３．Duffing振子の位相空間上のストレンジ・アトラクタに対するフラクタル次元
• ２－１．DLAによる樹木状クラスタのシミュレーション
• ２－２．DLAによる樹木状クラスタのフラクタル次元

第２章　対称ポテンシャルによる量子散乱

ゴール：水素原子のクリプトン原子による散乱に対する散乱断面積の計算

• ・ヌメロフ法による常微分方程式の解法
• ・球ベッセル関数
• ・ルジャンドル多項式
• ・位相シフト→断面積を計算するアルゴリズム

その他

• ・擬似乱数生成器：メルセンヌ・ツイスタの使い方
• ・ランダムウォークによる擬似乱数の比較：C言語rand関数とメルセンヌ・ツイスタ(mt19937ar)