一様媒質中における一般解と具体例
【1-3】1軸ガウシアンによる光パルスと電子パルス
前節「【1-2】平面波の時間発展」では、平面波の時間発展をアニメーション化しました。 第1章「1.一様媒質中における一般解と具体例」では、z-x平面をz軸から角度θ方向に伝搬する3種類のパルス型と2種類のビーム型を具体例として考えます。
3種のパルスと2種のビームの定義
3種のパルス
本稿では3種類のパルス型を
■1軸ガウシアンによるパルス
■2軸ガウシアンによるパルス
■3軸ガウシアンによるパルス
と呼ぶことにします。
波の進行方向をz-x平面とする場合、3次元空間 x-y-zの3軸をとり直して、
波の進行方向、波の進行方向の垂直方向とy軸方向の3軸と考えることができます。
この3つの軸を用いることによって3種のパルスを定義します。
一つ目の「1軸ガウシアンによるパルス」を波の進行方向の1軸に対して空間的に振幅がガウス分布する形状と定義します。
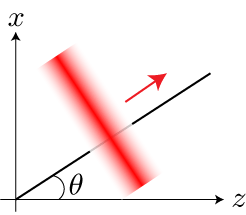
「1軸ガウシアンによるパルス」は波の進行方向に対する垂直方向とy軸方向には、同じ振幅で無限に続いていることを意味します。 次に「2軸ガウシアンによるパルス」は波の進行方向と垂直方向の2軸に対して空間的に振幅がガウス分布する形状と定義します。
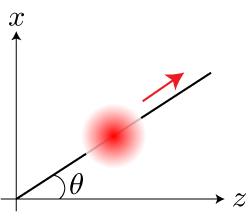
「2軸ガウシアンによるパルス」y軸方向には同じ振幅で無限に続いている円柱形であることを意味します。 最後に「3軸ガウシアンによるパルス」は波の進行方向、垂直方向と y軸の3軸に対して空間的に振幅がガウス分布る形状と定義します。 つまり、楕円球状のパルスとなります。
2種のビーム
本稿では2種類のビーム型を
■垂直1軸ガウシアンによるビーム
■垂直2軸ガウシアンによるビーム
と呼ぶことにします。
パルス型と同様、波の進行方向をz-x平面として波の進行方向、波の進行方向の垂直方向とy軸方向の3軸を考えます。
一つ目の「垂直1軸ガウシアンによるビーム」は波の進行方向と垂直方向の1軸に対して空間的に振幅がガウス分布する形状と定義します。
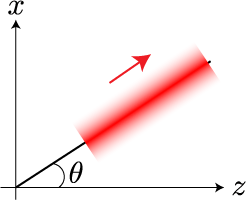
「垂直1軸ガウシアンによるビーム」はy軸方向には同じ振幅で無限に続いている板状であることを意味します。 次の「垂直2軸ガウシアンによるビーム」は波の進行方向の垂直方向とy軸の2軸に対して空間的に振幅がガウス分布する形状と定義します。 つまり、楕円円柱形状のビームとなります。
1軸ガウシアンによるパルスの表式
波数ベクトルの分解
前節同様、【1-1】一般解の表式で示した一様媒質中のマクスウェル方程式と一様ポテンシャル中のシュレディンガー方程式の一般的表式
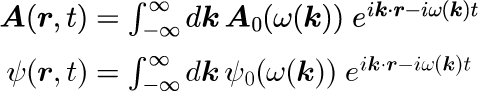
と分散関係
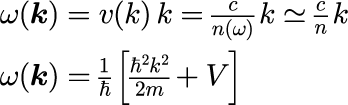
から始めます。 z-x平面をz軸から角度θ方向に伝搬するパルスを考えるために、任意の波数ベクトル k を波の進行方向を与える k_0 を基準として、波の進行方向と並行の k_||、波の進行方向と垂直の k_⊥、y軸方向の k_y の3軸に分解します。
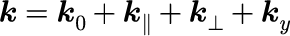
波数ベクトルの関係を図示すると
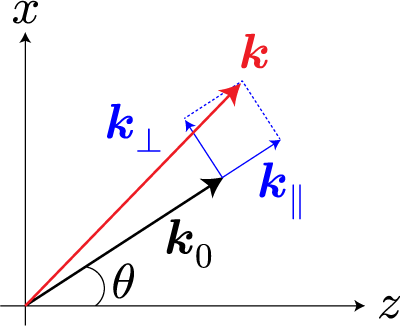
となります。波数ベクトルの成分をすべて明示的に書くと
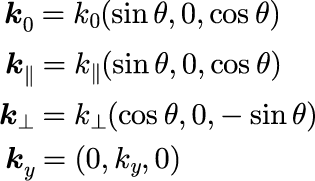
となります。
式(1)の係数の与え方
平面波同様、式(1)の係数A_0とψ_0の与え方で、z-x平面をz軸から角度θ方向に伝搬する「1軸ガウシアンによるパルス」を作り出すことができます。 具体的には
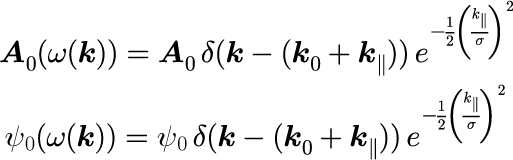
となります。k_0 はガウス分布の中心となる波数ベクトルで k_|| は波の進行方向の波数ベクトルを表します。 1軸ガウシアンによるパルスの時間発展を与える表式の導出する上での準備が完了しました。
1軸ガウシアンによるパルスの時間発展を与える表式の導出
1軸ガウシアンによるパルスの時間発展を与える表式の導出を手順を踏んで示します。 はじめに、式(5)に式(1)を代入すると
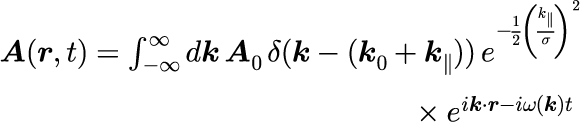
となります。波数ベクトル k の積分範囲は波数空間の全領域ですが、 実際に足し合わせる波数空間はデルタ関数の条件を満たす領域に制限されるます。 積分を実行するために、積分変数を
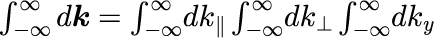
とします。 式(7)と式(3)を式(6)に代入すると
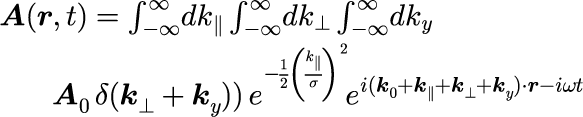
となります。波数ベクトル k_⊥ と k_y は直交するので、デルタ関数の中身が0となるためには、
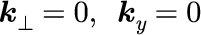
を満たす必要があります。つまり、k_⊥ と k_y に関して直ちに積分することができて、
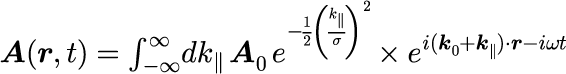
が得られます。実際に数値計算を行うため、式(4)を用いてベクトルの成分で式(10)変形すると
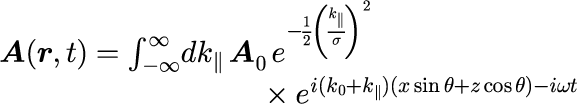
となります。式(3),(4)を考慮すると波数ベクトル k は
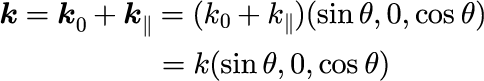
となるので、式(11)を変数変換し、最終的には
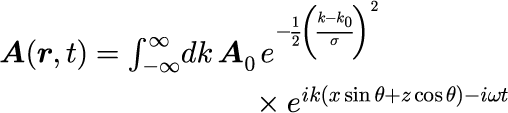
となります。電子の場合も同様に計算することができ、
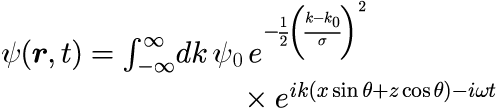
となります。ただし、角振動数ωは分散関係(式(2))を満たします。
波数空間と実空間
式(5)のσは波数ベクトル k の波数空間におけるガウス分布の幅を決めるパラメータとなります。 σの次元は波数ベクトル同様 [rad/m]です。 式(13)と式(14)の積分は解析的に計算することができ、その結果から実空間における光パルスの幅が得られます。
光パルスの波数空間の幅と実空間の幅の関係
式(13)の積分結果は
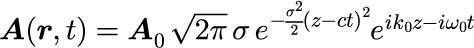
となります。式(15)をみると実空間におけるガウス分布と、波数分布の中心波数 k_0 による平面波の積となっていることがわかります。 t = 0 で z = 0 を中心とし、光速 c で進行する光パルスであることがわかります。 式(13)と式(15)より波数空間と実空間における半値全幅を求めることができます。
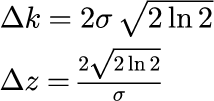
σが大きいほど波数空間における幅が大きくなり、実空間での幅が小さくなります。 波数空間と実空間の半値全幅は反比例の関係であり、積は一定値となります。
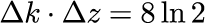
次のグラフはσ=10^{14}/c とした場合の波数空間と実空間の幅の関係です。 ただし、k_0 や A_0 は【1-2】平面波の時間発展と同じです。
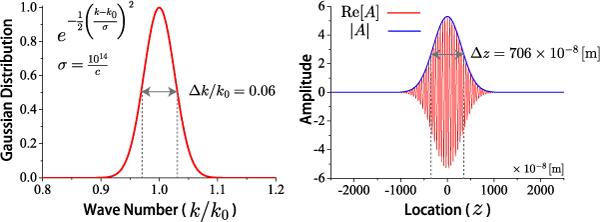
波数空間と実空間における半値全幅は式(16)で計算することができます。
電子パルスの波数空間の幅と実空間の幅の関係
光パルスと同様に、式(14)の積分を計算します。
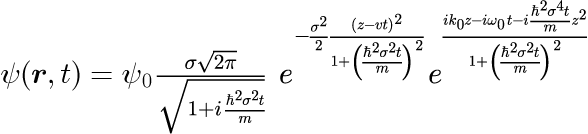
式(18)は実空間におけるガウス分布と、変調された波数分布の中心波数 k_0 による平面波の積となっていることがわかります。 光パルスの場合、式(15)で示したとおり光速 c で進行するパルスでしたが、 電子パルスの場合には、
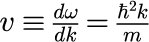
で定義される群速度で進行するパルスとなります。 これは式(18)から分かる通り、電子パルスは光パルスの違いは時刻と共にパルス幅が広がっていきます。 このことは式(18)から得られる波数空間と実空間における半値全幅
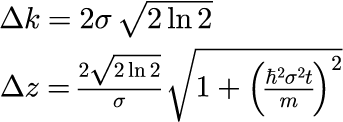
の時間依存性を見れば明らかです。 波数空間の幅は時間 t に依存しない一方で、実空間における幅は時間 t の1/2乗に比例して広がっていききます。 さらに、広がり方はσに比例することがわかります。 これは t=0 における実空間の幅が狭いほど広がり方が早いことを意味します。 また、光パルスと同様、波数空間と実空間の半値全幅は反比例の関係であり、積は次のようになります。
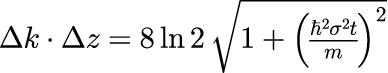
最後に波数空間と実空間の幅の関係です。 ただし、k_0 や ψ_0 は【1-2】平面波の時間発展と同じです。
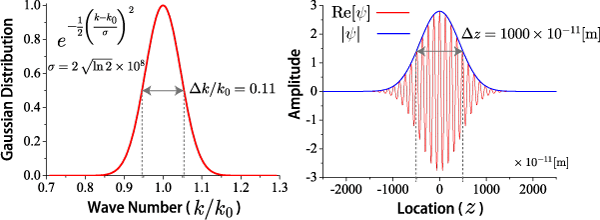
波数空間と実空間における半値全幅は式(20)で計算することができます。
光および電子による1軸パルスの時間発展
式(13),(14)のσに適切なパラメータを適用することで一様媒質中の光および電子による平面波の時間発展を計算することができます。
光による1軸パルスの時間発展
k_0 や A_0 は【1-2】平面波の時間発展と同じです。 入射角度θ = 0°~ 80°の値で計算した結果を示します。 図のx-y軸のスケールは ×10^{-8}[m] で、時間間隔は 10^{-6}/c ≒ 3.3×10^{-15}[s]。
θ=0°
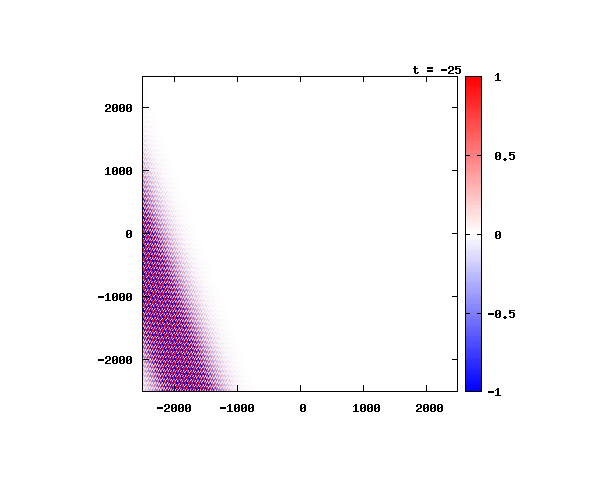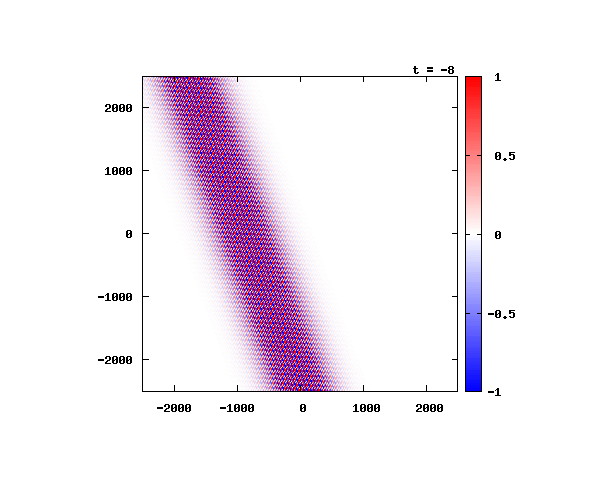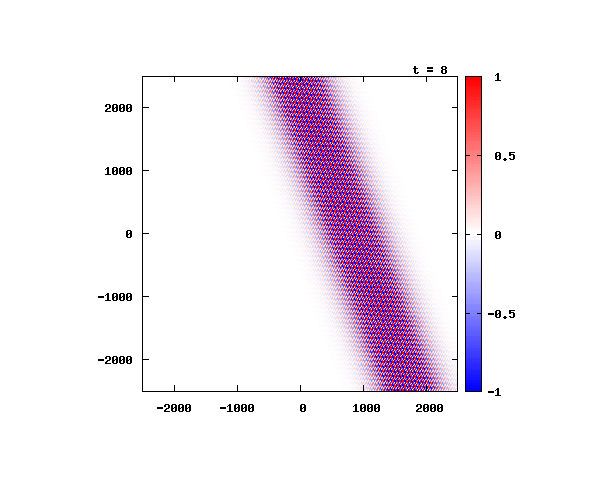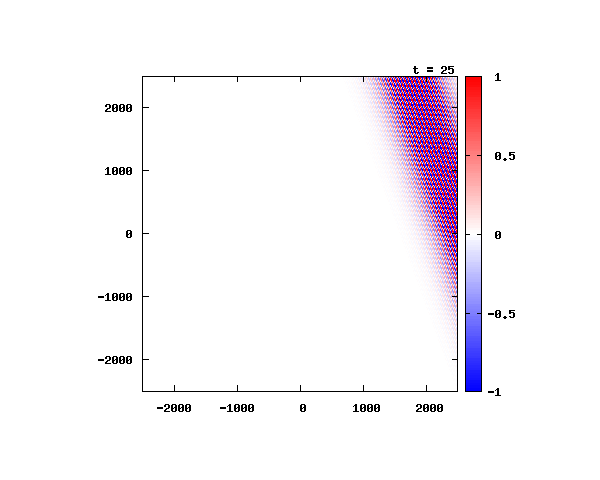
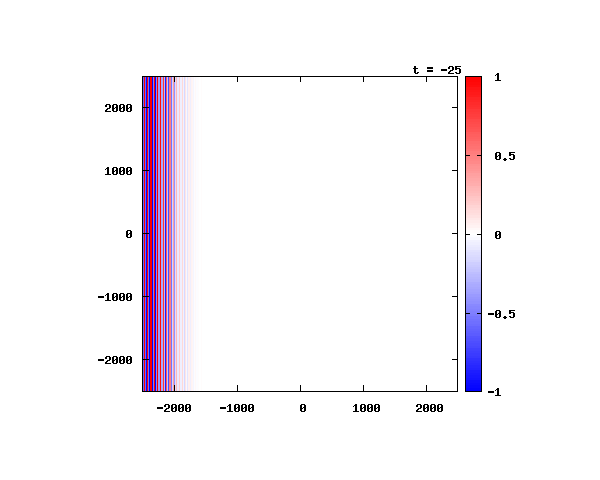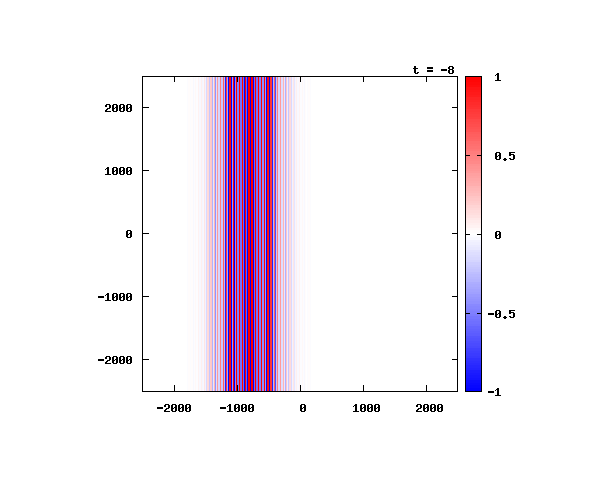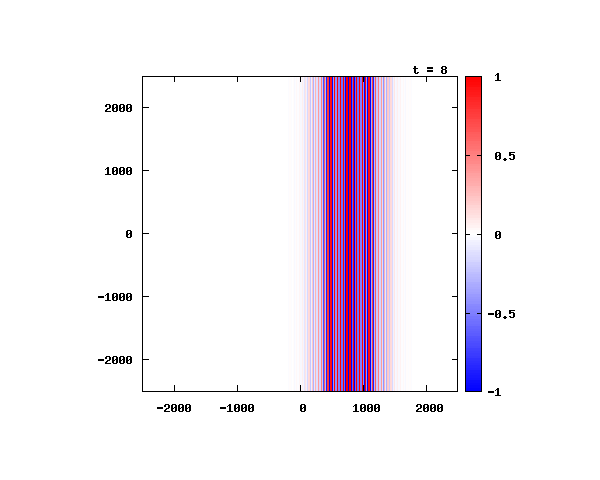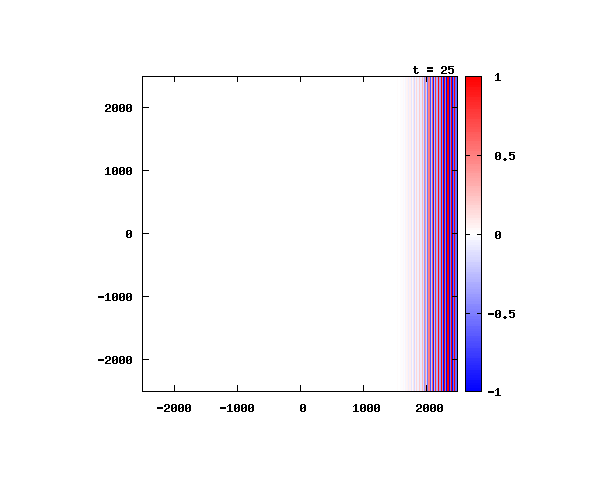 θ=20°
θ=20°
 θ=40°
θ=40°
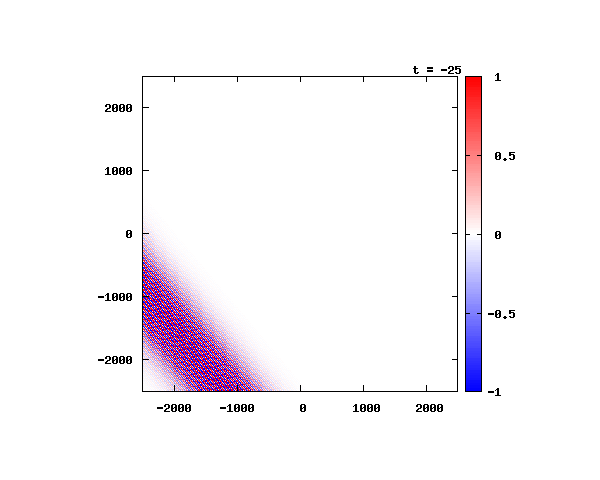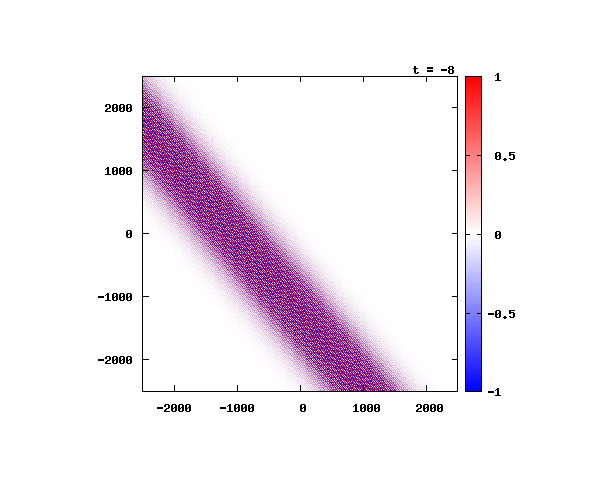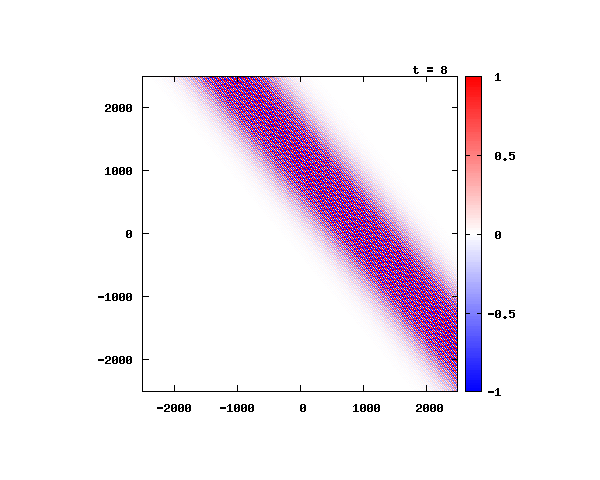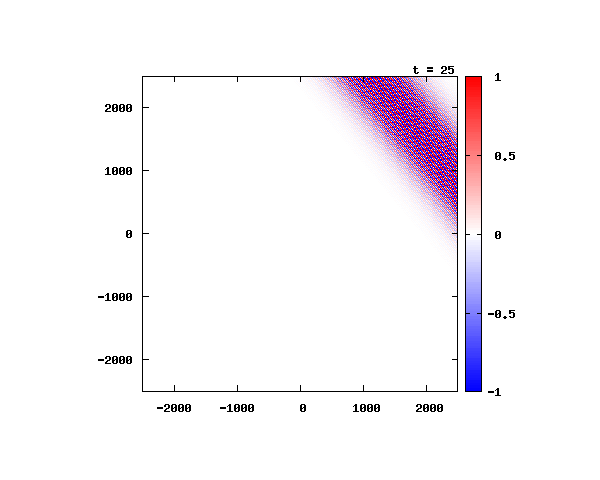 θ=60°
θ=60°
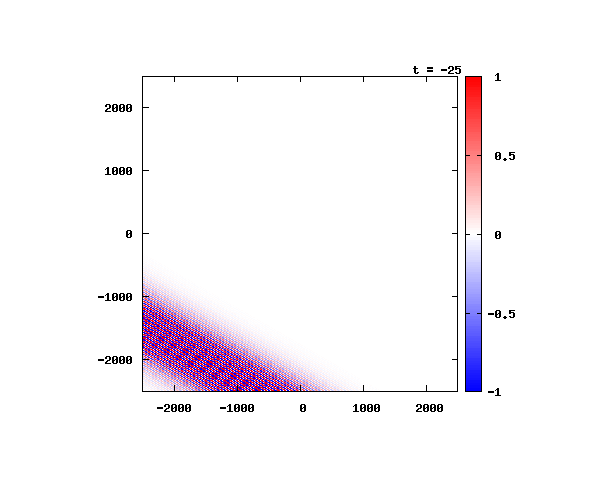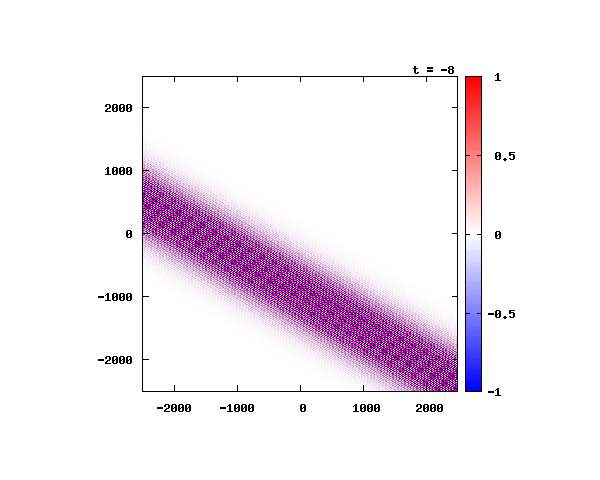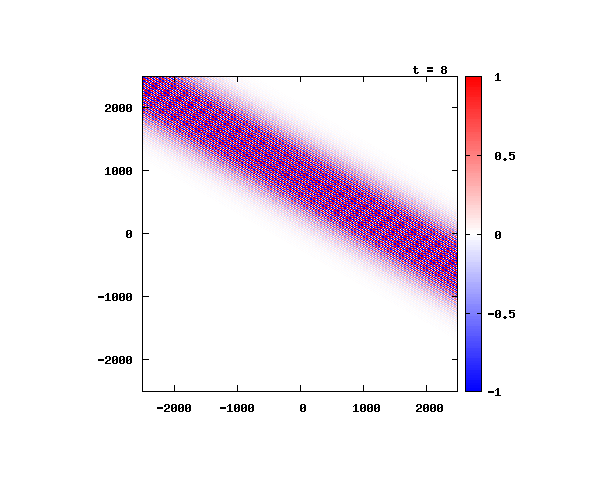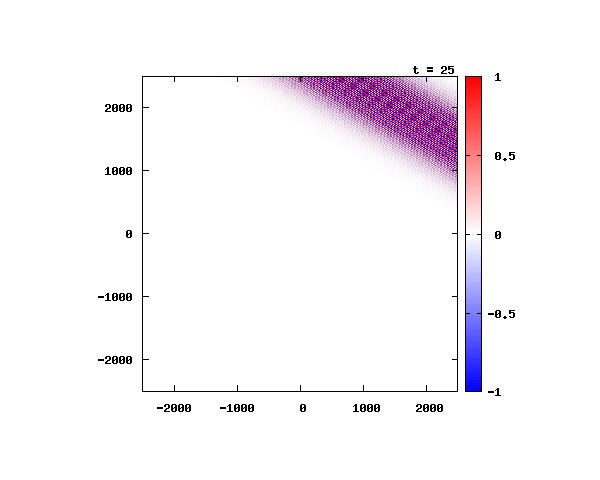 θ=80°
θ=80°
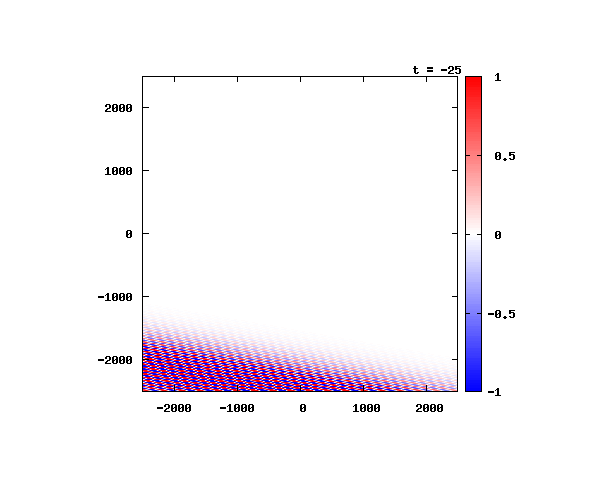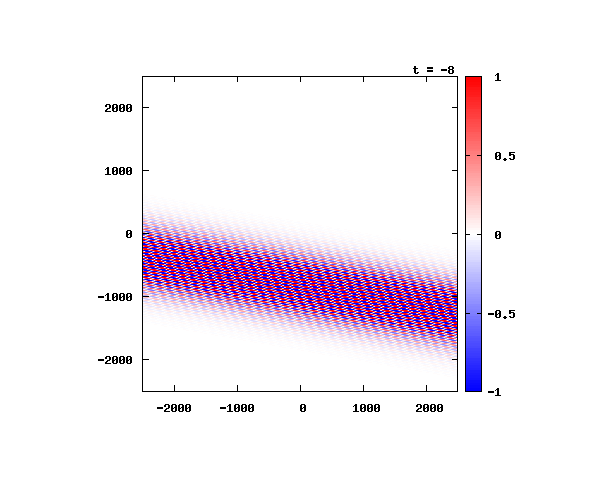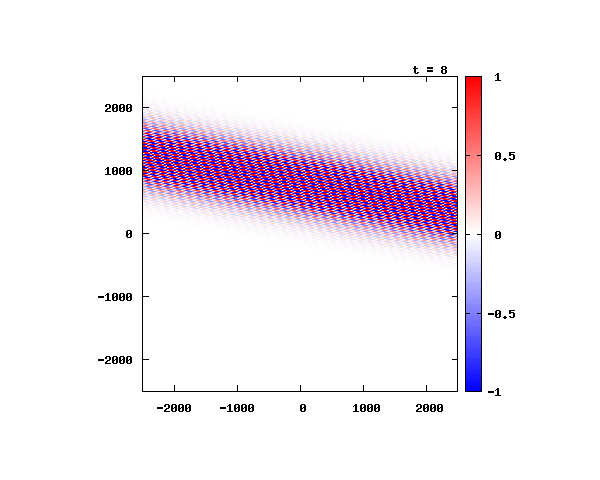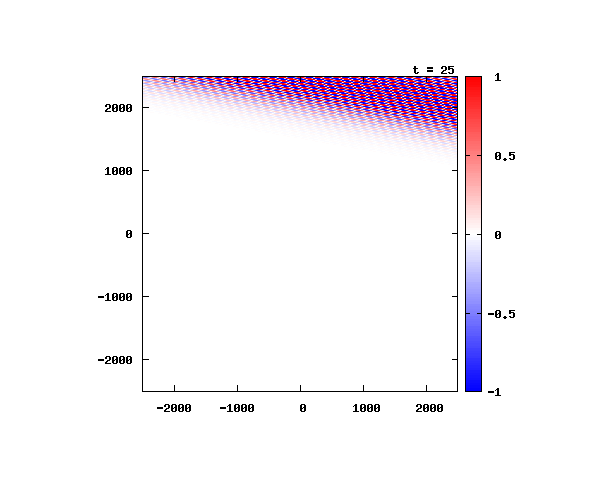
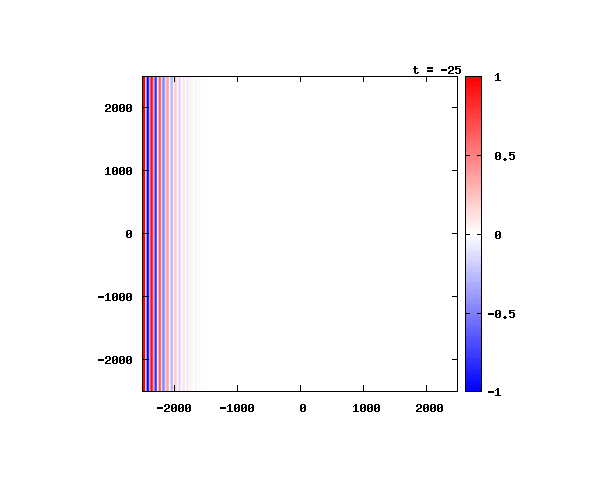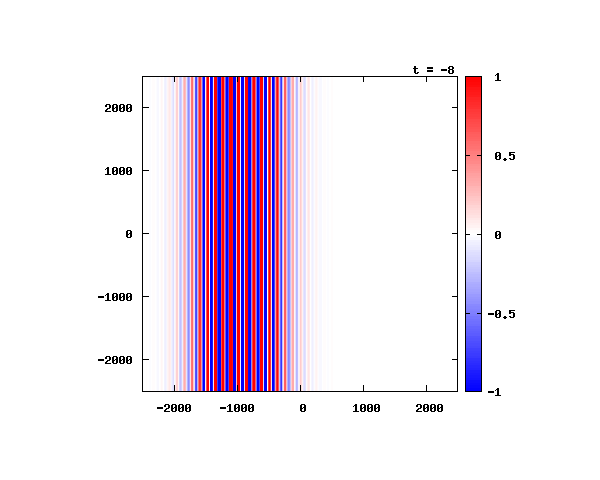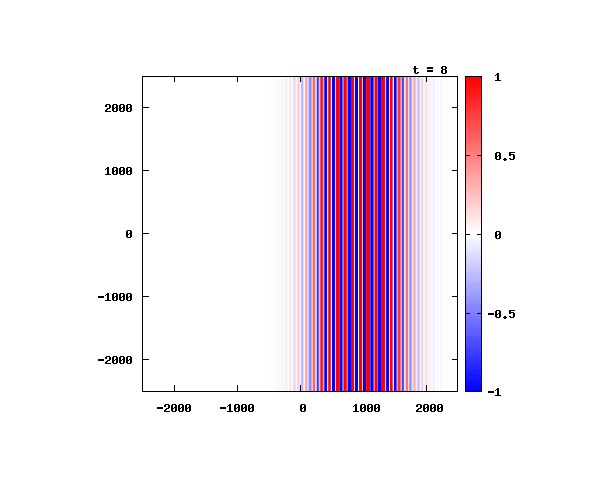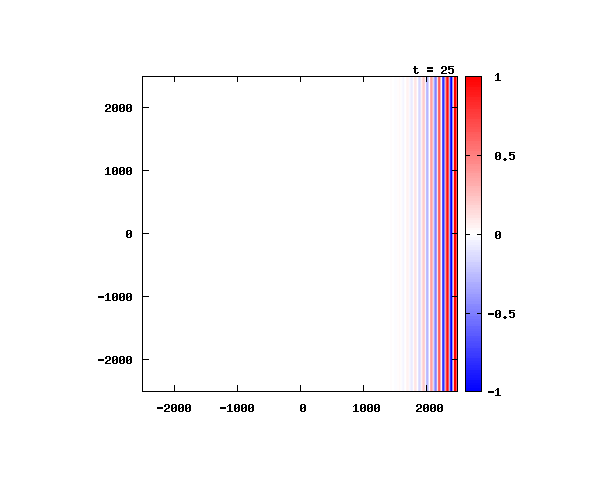
電子による1軸パルスの時間発展
k_0 や ψ_0 は【1-2】平面波の時間発展と同じです。 入射角度θ = 0°~ 80°の値で計算した結果を示します。 図のx-y軸のスケールは ×10^{-11}[m] で、時間間隔は 2×10^{-15}[s]。
θ=0°
 θ=20°
θ=20°
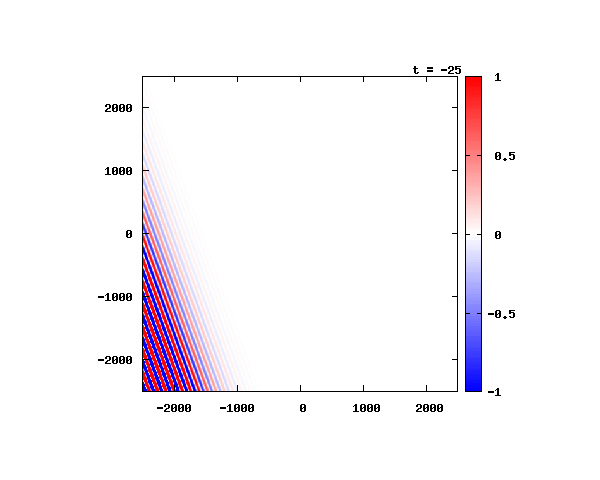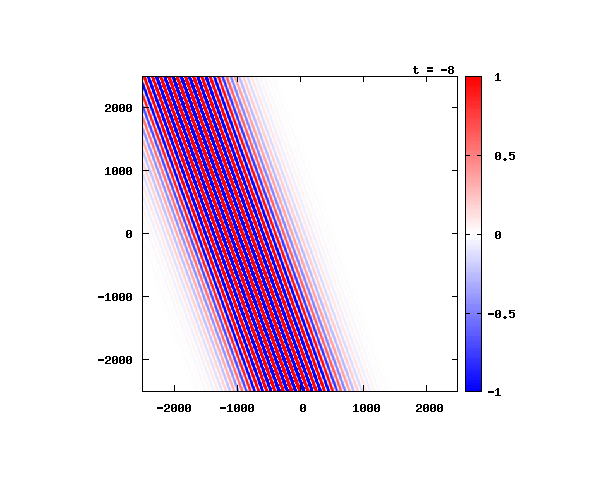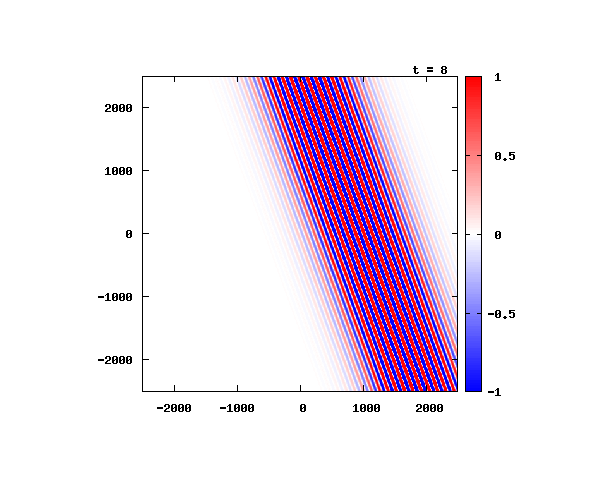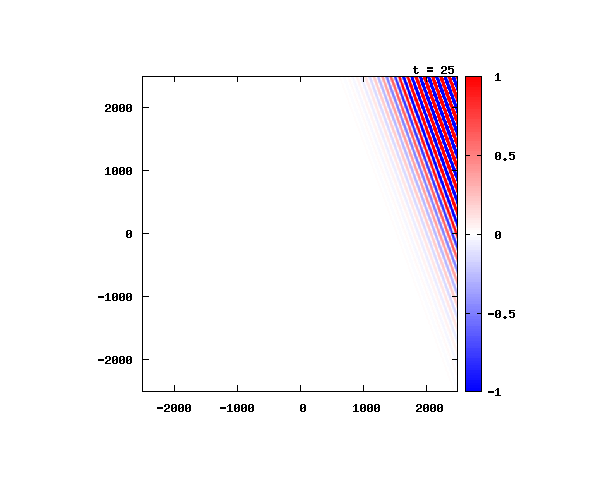 θ=40°
θ=40°
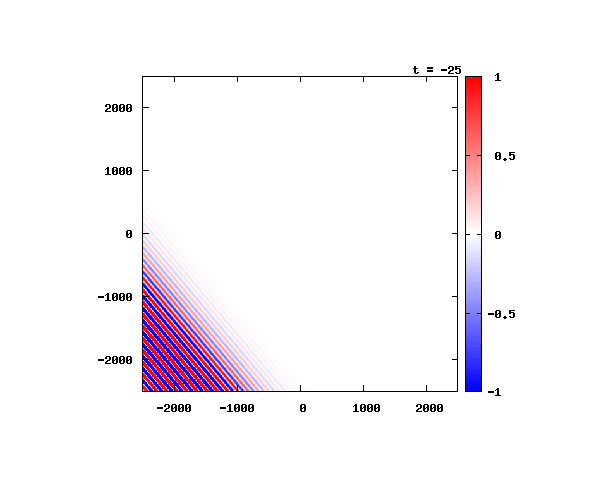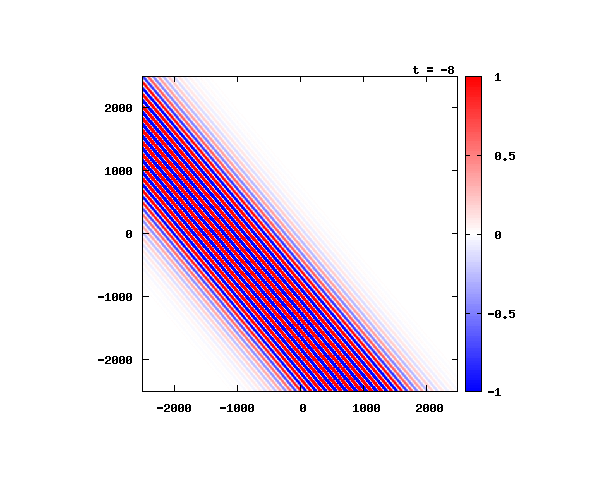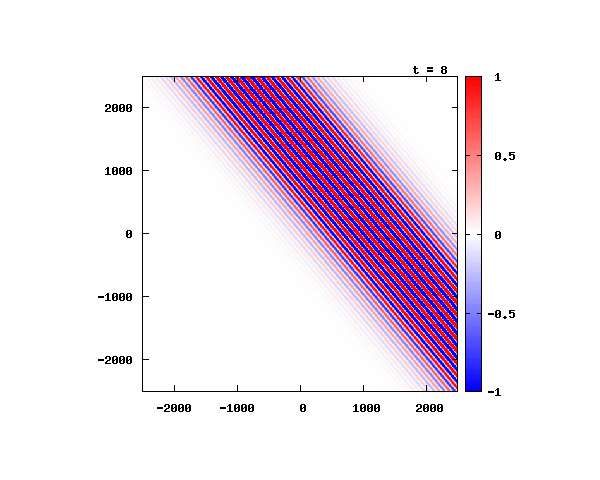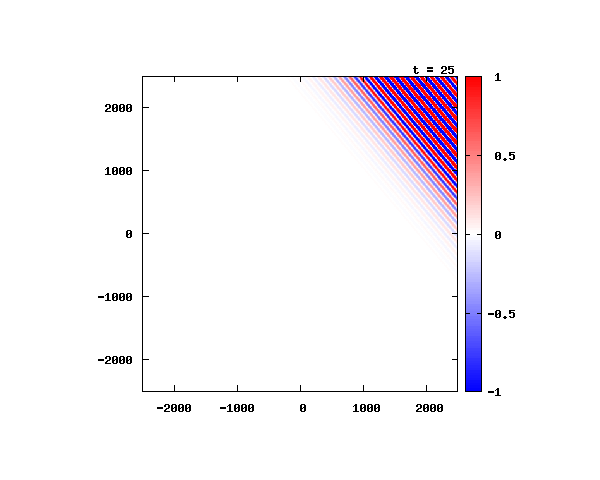 θ=60°
θ=60°
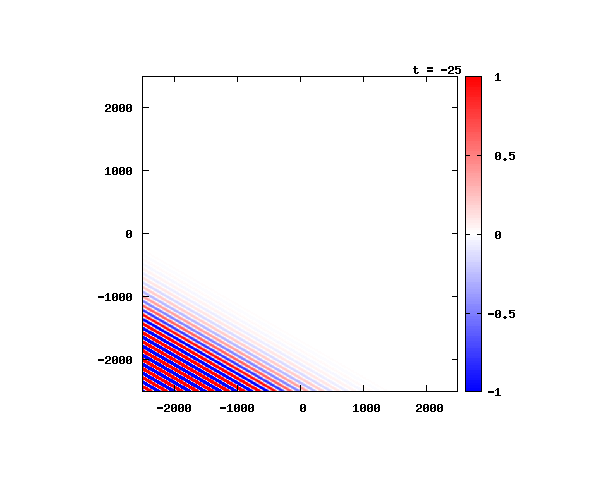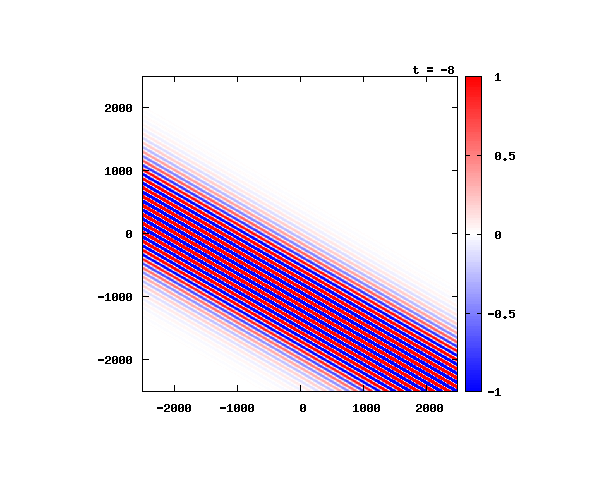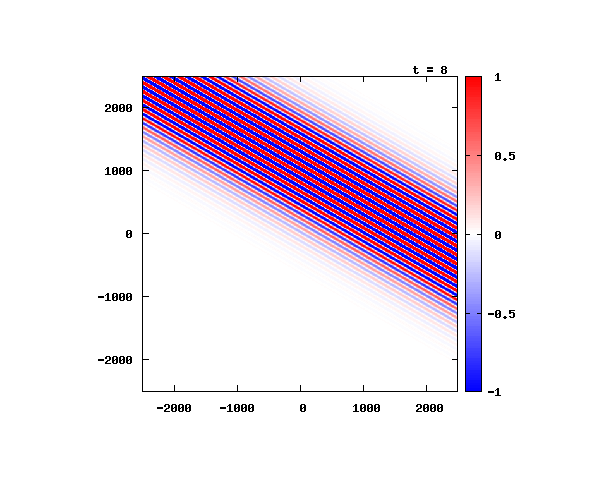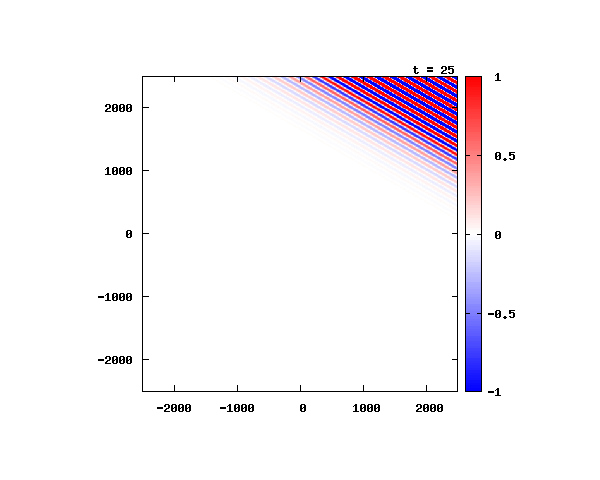 θ=80°
θ=80°
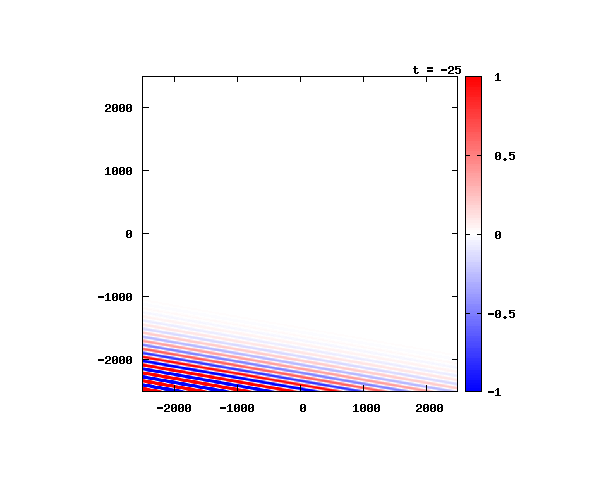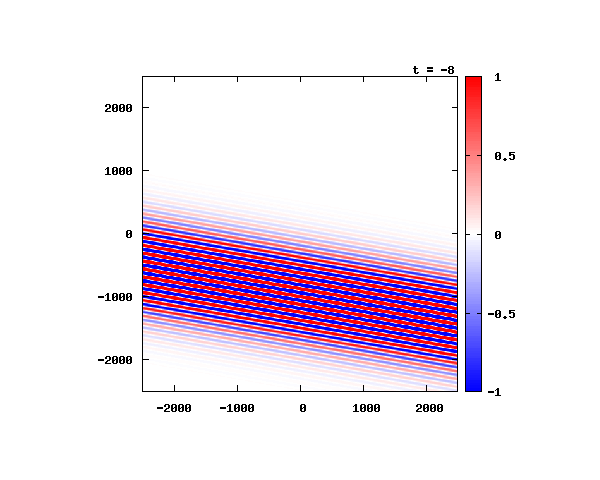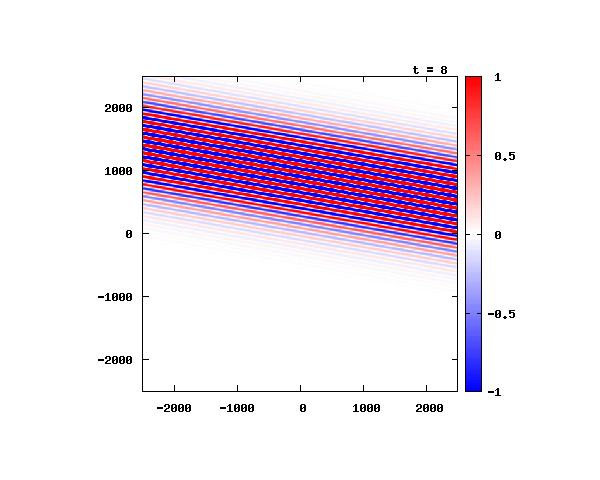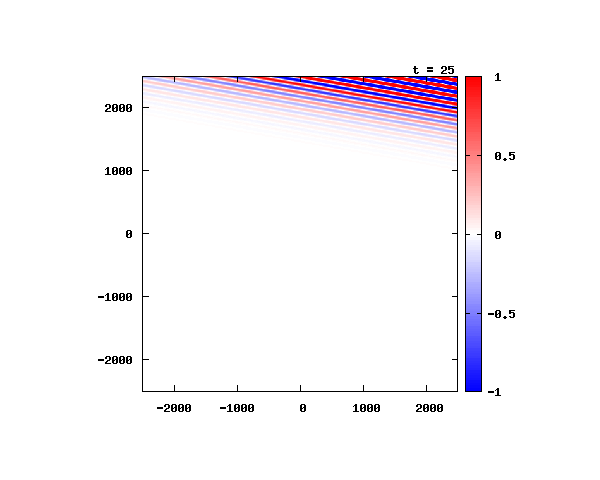
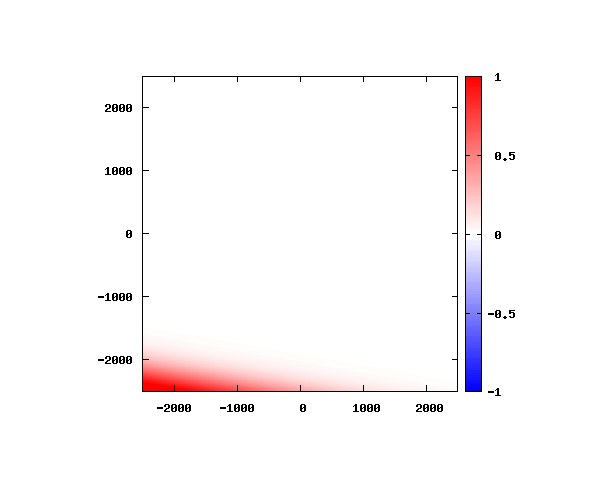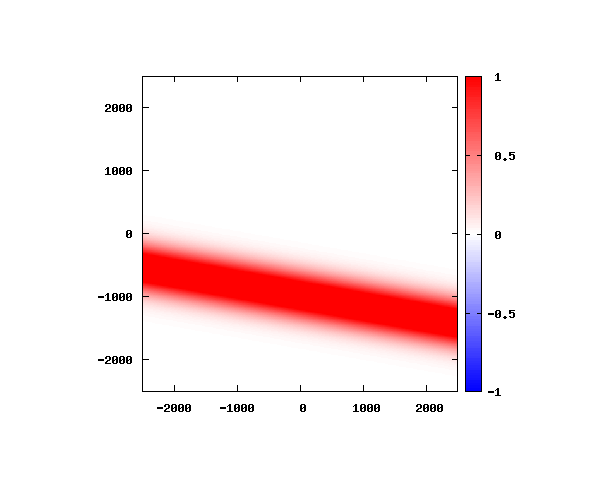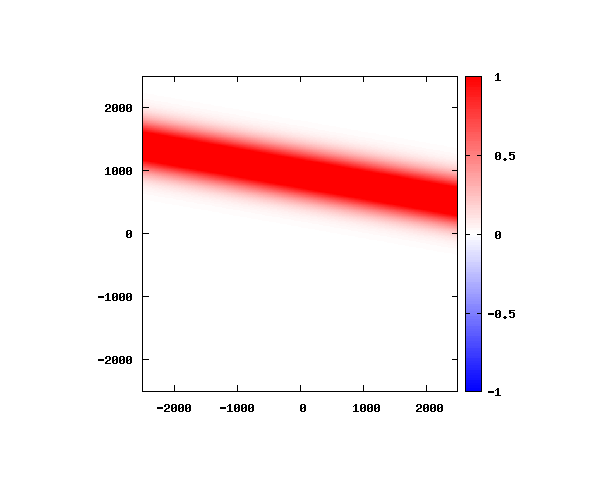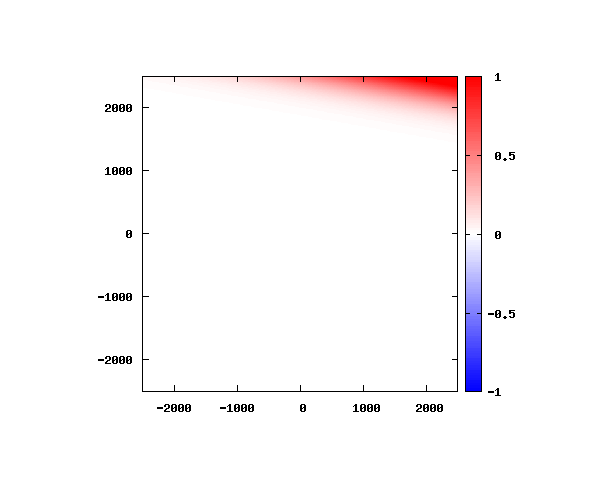
電子の波動関数の絶対値
図のx-y軸のスケールは ×10^{-11}[m] です。
θ=0°
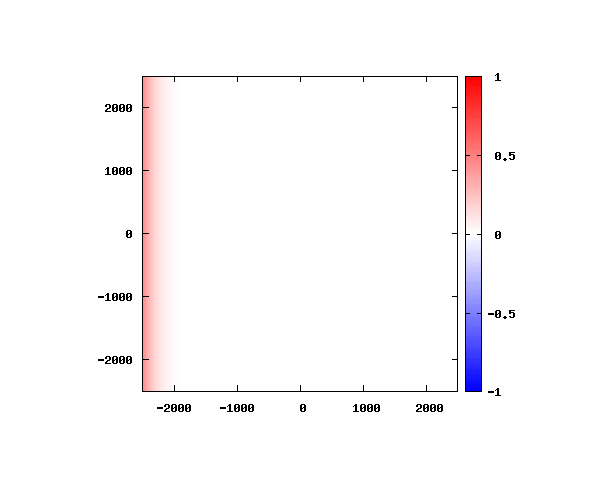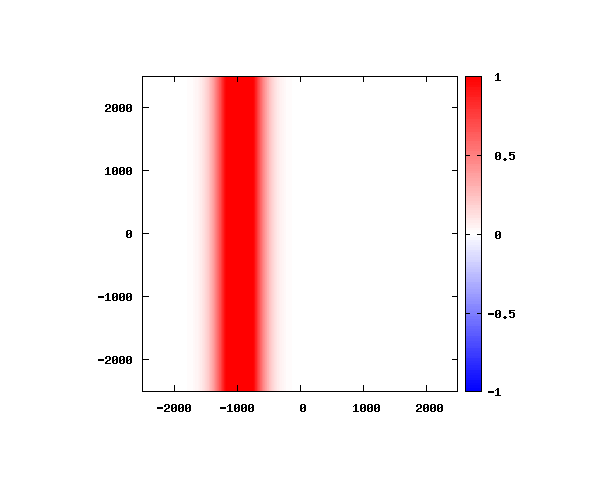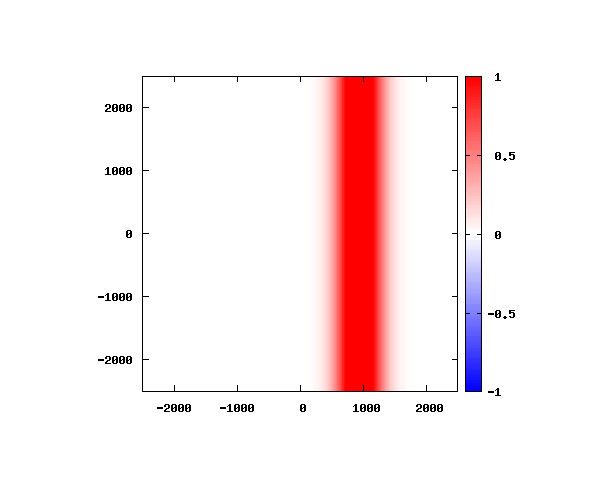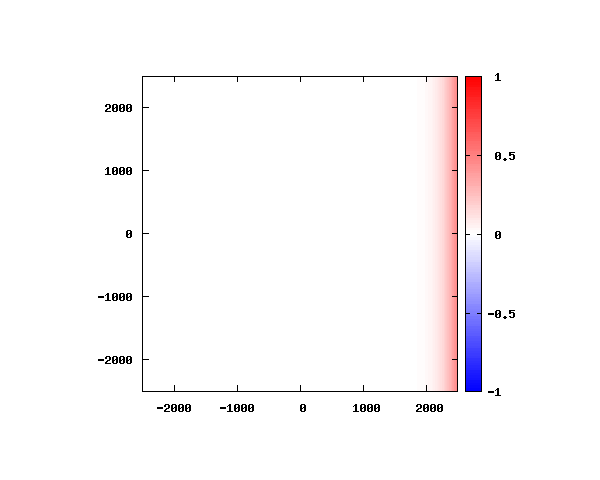 θ=20°
θ=20°
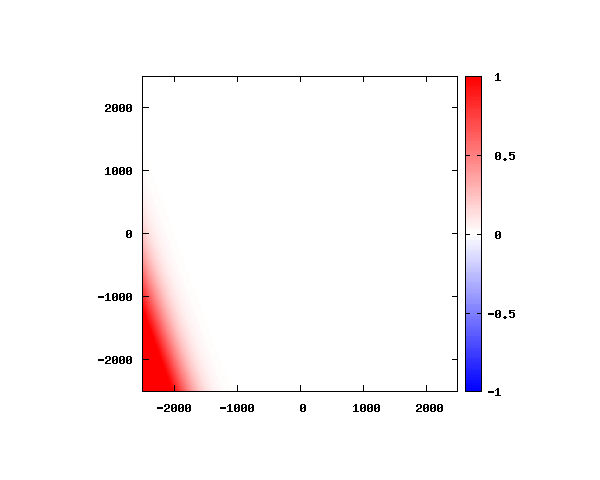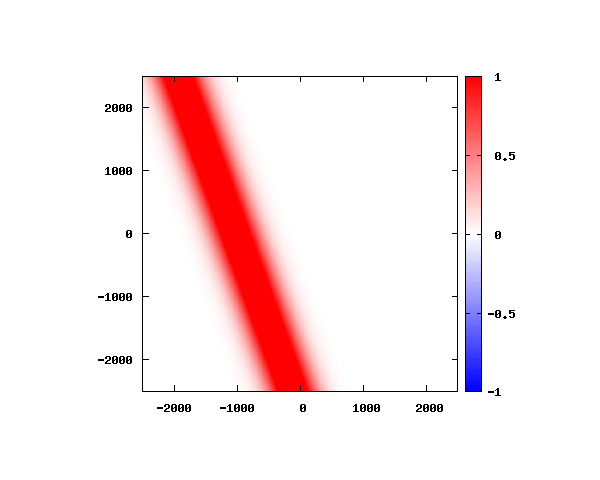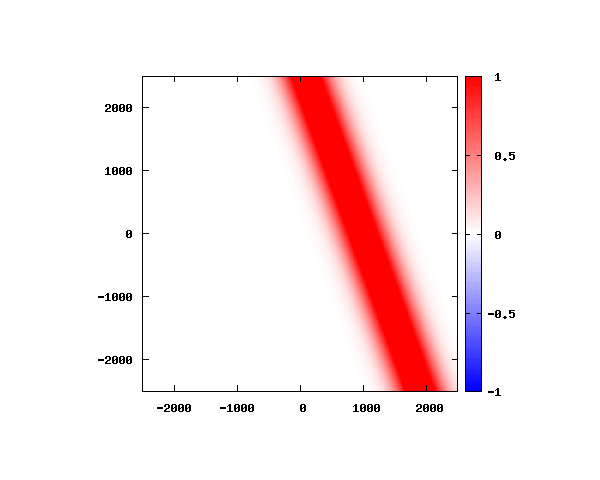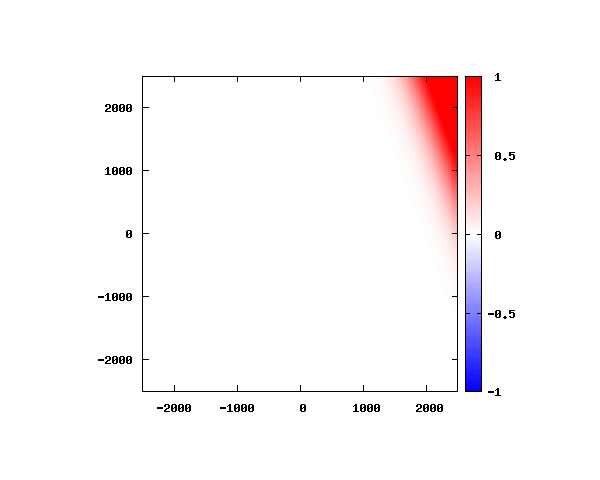 θ=40°
θ=40°
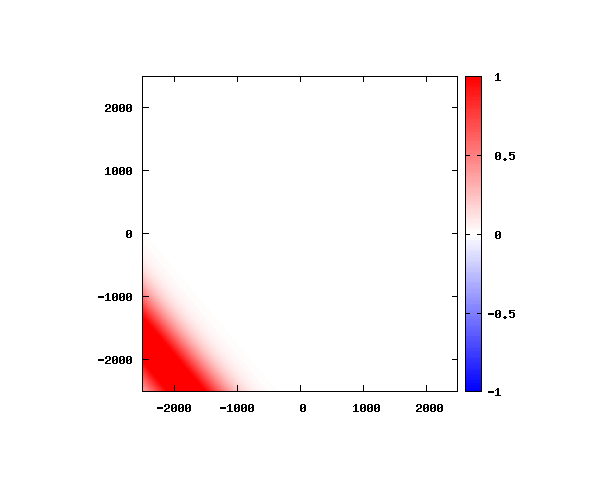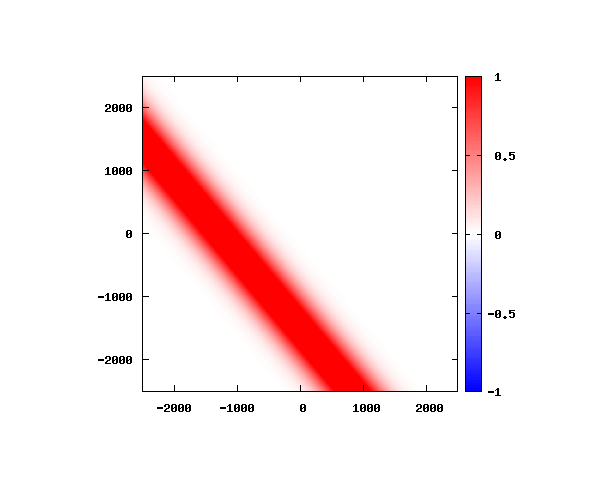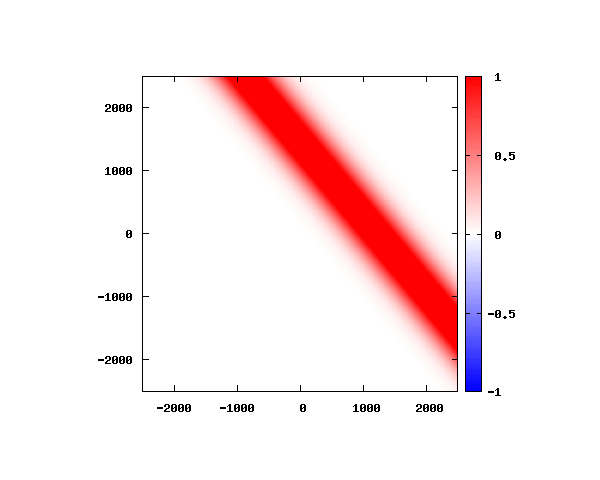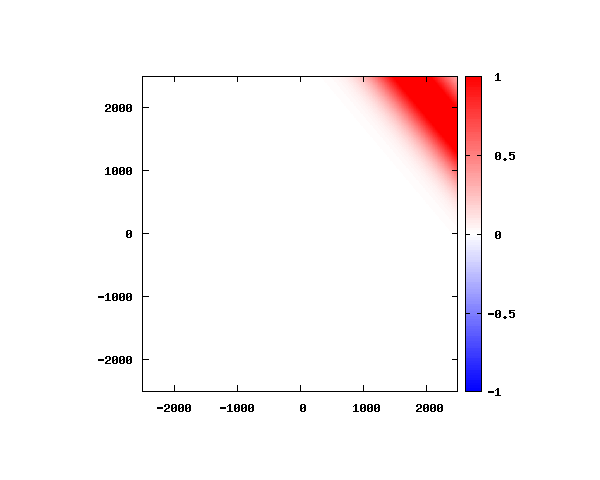 θ=60°
θ=60°
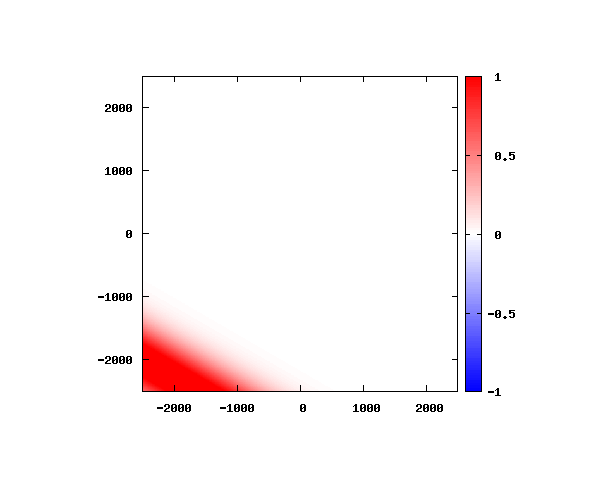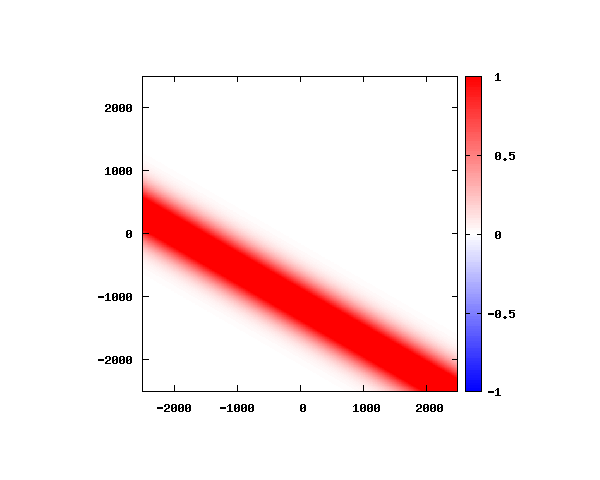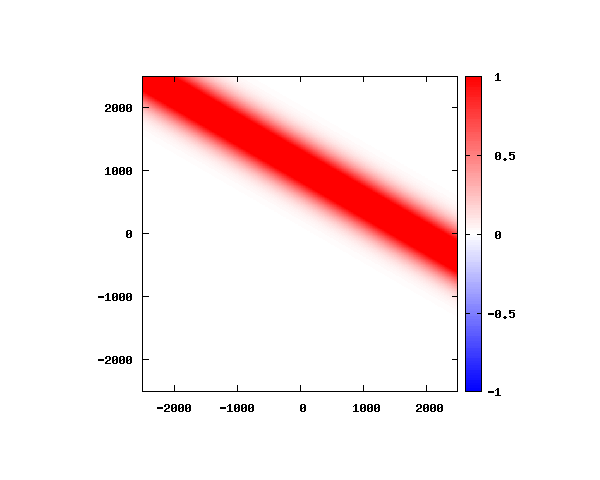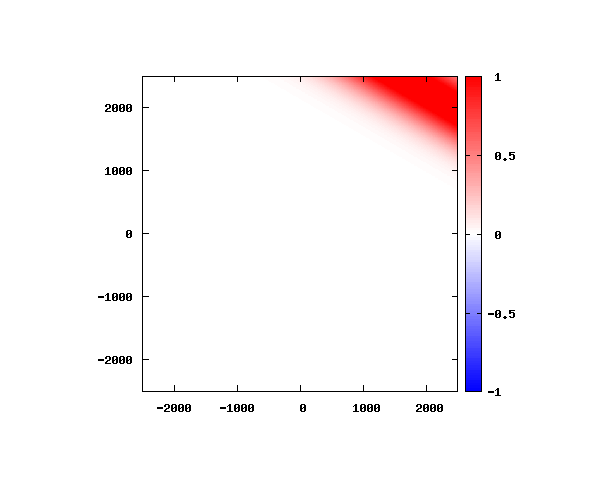 θ=80°
θ=80°
プログラムソースたち
C++プログラムソースのとおりです。
C++
■光の1軸パルスMaxwell_pulse1.cpp
■電子の1軸パルスSchrodinger_pulse1.cpp
VisualC++のプロジェクトファイル
■光の1軸パルスMaxwell_pulse1.zip
■電子の1軸パルスSchrodinger_pulse1.zip
gnuplot テンプレート
【目次】シュレディンガー方程式とマクスウェル方程式
- 0.導入
【0-1】はじめに
【0-2】本稿で取り扱う基礎方程式 -
1.一様媒質中における一般解と具体例
【1-1】一般解の表式
【1-2】平面波の時間発展
【1-3】1軸ガウシアンによる光パルスと電子パルス (1軸ガウシアンによる電子パルスの拡散)
【1-4】2軸ガウシアンによる光パルスと電子パルス (2軸ガウシアンによる電子パルスの拡散, 2軸ガウシアンによる光パルスの拡散)
【1-5】3軸ガウシアンによる光パルスと電子パルス
【1-6】垂直1軸ガウシアンによる光ビームと電子ビーム
【1-7】垂直2軸ガウシアンによる光ビームと電子ビーム
【1-8】直線偏光と円偏光
-
2.異なる媒質の境界における電磁波と電子波
【2-1】異なる媒質の境界における波動の一般論
【2-2】電磁波に対する透過係数と反射係数の導出
【2-3】電子波に対する透過係数と反射係数の導出
【2-4】境界面において任意の形状の波に対して時間発展を与える一般表式
【2-5】境界面における平面波電磁波の時間発展
【2-6】境界面における平面波電子波の時間発展
【2-7】境界面における1軸ガウシアンによる光パルスと電子パルスの時間発展
【2-8】境界面における2軸ガウシアンによる光パルスと電子パルスの時間発展
【2-9】境界面における3軸ガウシアンによる光パルスと電子パルスの時間発展
【2-10】境界面における垂直1軸ガウシアンによる光ビームと電子ビームの時間発展
【2-11】境界面における垂直2軸ガウシアンによる光ビームと電子ビームの時間発展
-
3.転送行列法
・電子のトンネル確率
・光のトンネル効果
- 4.1層バリアにおける光パルスと電子パルスのシミュレーション
- 5・ポテンシャル障壁による量子粒子のトンネル時間
- 6・フォトニックバンドギャップによる光パルスのトンネル時間
-
7.無限周期構造中の分散関係,群速度,位相速度
・転送行列とブロッホの定理
・ブロッホ波数と透過係数の関係
・分散関係
・透過係数と群速度の関係
-
8.有限サイズの結晶における光パルスと電子パルスの横断時間
・光パルスと電子パルスの横断時間の導出
・パルス伝搬速度と群速度の関係
-
9.フォトニックバンド端における光パルスの遅延
・1次元フォトニック結晶における透過係数と横断時間の数値計算
・横断時間の解析解
-
10.バンド端における電子パルスの遅延
・1次元クローニッヒ・ペニーモデルにおける透過係数と横断時間の数値計算
・横断時間の解析解
- 11.非周期構造における光パルスと電子パルスと伝搬
































