任意の関数をエルミート多項式で展開する
任意の関数を f(x) とします。 規格化エルミートの異なる次数同士の内積は直交するため、f(x)は規格化エルミート多項式の和で表すことができます。 本稿では f(x) を規格化エルミート多項式を用いて
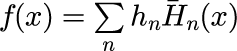
と表すことができるとします。ここで h_n は規格化エルミート多項式の展開係数です。 規格化エルミート多項式は「エルミート多項式の規格化」で示した直交条件を満たすので、式(1)の両辺に H_m(x) をかけて積分することで展開係数 h_n が得られます。
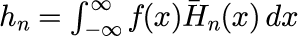
式(2) を式(1)に代入することで元の関数 f(x) になることがわかります。 h_n は 関数 f(x) と 規格化エルミート H_n(x) の内積を表します。 解析的には式(2)の和と式(3)の積分は無限区間で実行できるため、無限制度で実施することができますが、数値的には和や積分は有限の値しか取り扱うことができません。 展開係数を数値的に得るには
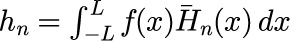
を計算します。L は積分範囲です。 本稿では得られた 展開係数 h_n を用いてどの程度再現できるかを確かめることにします。
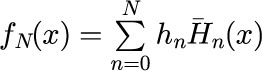
ここで、N は和の上限を表し、f_N(x) は展開係数から逆変換して元の関数を再現した関数となります。
計算結果
本稿ではf(x) の具体例としてガウス分布とステップ関数の規格化エルミート多項式の展開係数と、 展開係数から逆変換して元の関数を再現します。
ガウス分布
本稿で取り扱うガウス分布を
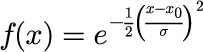
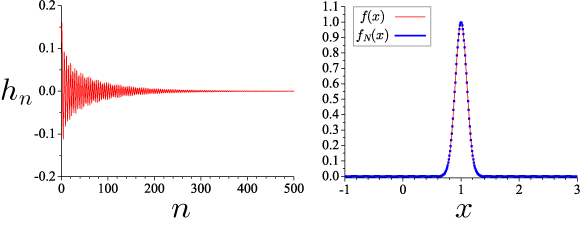
とします。x_0 = 1.0 はガウス分布を中心座標で、σ=0.1 はガウス分布の幅を決めるパラメータです。 次の図は、展開係数 h_n と 逆変換して元の関数を再現した結果です(N=500, L=20)。
右図は元の関数 f(x) と h_n の逆変換で再現した関数 f_N(x) です。 ガウス分布の場合、N=500, L 20 程度で十分に元の関数を再現していることわかります。
ステップ関数
2つ目の具体例は
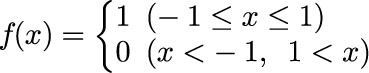
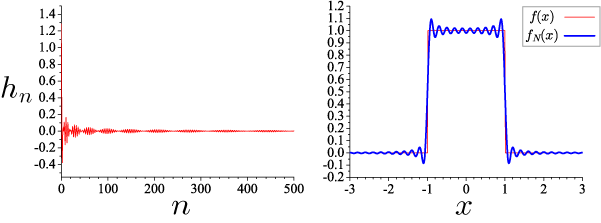
で定義されるステップ関数です。 次の図は、ガウス分布同様、展開係数 h_n と 逆変換して元の関数を再現した結果です(N=500, L=20)。
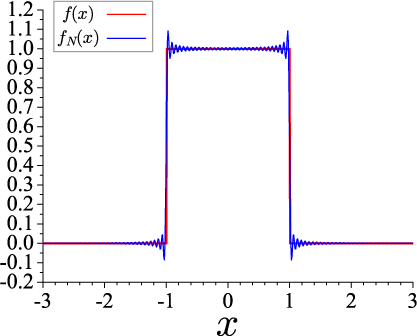
右図は元の関数 f(x) と h_n の逆変換で再現した関数 f_N(x) ですが、再現度が低いようです。 より高次の展開係数まで計算して、元の関数を再現してみます(N=5000)。
N=500 と比べると、再現度は上がっているようです。 ステップ関数のように不連続関数の場合、不連続点での飛びが顕著に現れるのは、フーリエ変換の時にも現れるギブスの現象と同じであると考えられます。
C言語プログラムソース
数値積分にはシンプソン法(シンプソン法を利用して積分を数値計算する) を用いています。
任意の関数をエルミート多項式で展開するプログラム
/*
任意の関数をエルミート多項式で展開する
(2011.11.05 公開)
*/
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include <cstdio>
#include <iomanip>
#include <stdio.h>
#include <complex>
#if defined(_OPENMP)
#include <omp.h>
#endif
#if defined(_MSC_VER)
#include <direct.h> // Windowsフォルダ作成用
#elif defined(__GNUC__)
#include <sys/stat.h> // UNIX系ディレクトリ作成用
#endif
using namespace std;
double PI = acos(-1.0);
double e = 2.7182818284590452354;
complex<double> I = complex<double>(0.0,1.0);
int kizami = 10000;
double L = 20;
double x0 = 1.0;
double sigma = 0.1;
const int N_max = 500;//エルミート多項式の項数
double h[N_max+1] = {0.0}; //エルミート多項式の係数
double x_min = -3;
double x_max = 3;
//関数のプロトタイプ
double NormalizedHermite( int n, double x ); //規格化エルミート多項式
double Simpson(double a, double b, int n);
//任意の関数
double f(double x){
return exp(-1.0/2.0 * pow(((x-x0)/sigma),2)); //ガウシアン
//if(x>=-1 && x<=1) return 1.0 ;
//else return 0.0 ;
}
//被積分関数
double Integrand(double x, int n){
return NormalizedHermite(n, x) * f(x) ;
}
string folder = "data";//作成するフォルダ名
int main(){
#if defined(_MSC_VER)
_mkdir(folder.c_str()); // Windowsフォルダ作成
#elif defined(__GNUC__)
mkdir(folder.c_str(), S_IRWXU | S_IRWXG | S_IRWXO); // UNIX系のディレクトリ作成
#endif
ofstream ofs( "Hermite_coefficient.data" );
ofstream ofs2( "Hermite_reverse.data" );
for(int n=0; n<=N_max; n++){
h[n] =Simpson( -L, L , n);
ofs << n << " " << h[n] << endl;
}
for(double x=x_min; x<=x_max; x+=0.01){
double fr = 0.0;
for(int n=0; n<=N_max; n++){
fr += h[n] * NormalizedHermite(n, x) ;
}
ofs2 << x << " " << fr << " " << f(x) << endl;
}
}
double NormalizedHermite( int n, double x )
{
double y0, y1, y2;
y0 = sqrt(1.0/sqrt(PI)) * exp(-pow(x,2)/2);
if( n==0 ) return y0;
y1 = sqrt(2.0/sqrt(PI)) * exp(-pow(x,2)/2) * x;
if( n==1 ) return y1;
for(int m = 2; m<=n; m++ ){
y2 = sqrt(2.0/double(m)) * x * y1 - sqrt(double(m-1)/double(m)) * y0;
y0 = y1;
y1 = y2;
}
return y2;
}
double Simpson(double a, double b, int n)
{
double ss1 =0.0;
for(int i=1; i<=kizami/2-1; i++){
double x = a + (b-a)/double(kizami) * double(2*i);
ss1 += Integrand(x, n);
}
double ss2 =0.0;
for(int i=1; i<=kizami/2; i++){
double x = a + (b-a)/double(kizami) * double(2*i-1);
ss2 += Integrand(x, n);
}
return (b-a)/(3.0*double(kizami)) * ( Integrand(a, n) + Integrand(b, n) + 2.0 * ss1 + 4.0 * ss2 );
}