１次元量子力学における調和振動子
任意の初期状態に対する時間発展

前節「単一エネルギーの時間発展」にて、 １次元量子力学における調和振動子における状態の時間発展の表式を導出しました。

(1)

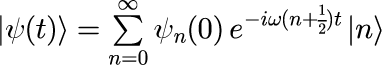
式(1)の両辺に位置演算子の固有ベクトルと内積をとる（左から<n|を掛ける）ことで、 座標表示の波動関数

(2)

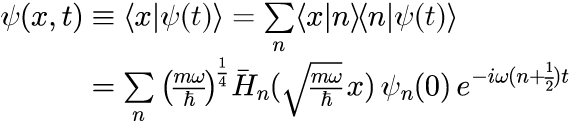
となります。 式(1)の ψ_n(0) は n に関して任意であり、状態の初期条件から決定することができます。 本節では、座標表示における波動関数の初期状態

(3)

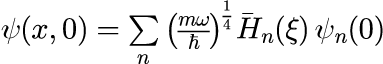
が、x = x_0 を中心としたガウス分布

(4)

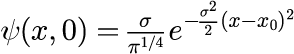
および、ステップ関数

(5)

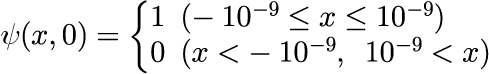
における ψ_n(0) を決定し、時間発展を計算することを行います。 ψ_n(0)の計算方法は、「任意の関数をエルミート多項式で展開する」で示したとおり、エルミート多項式の直交性を利用します。 初期状態がガウス分布の場合、式(3)に式(4)に代入し、両辺に規格化エルミートを掛けて積分することで、 ψ_n(0)は

(6)

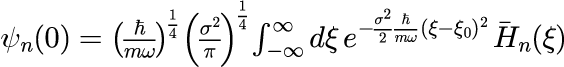
で計算することができます。 ただし、

(7)

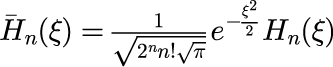
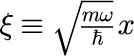
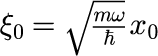
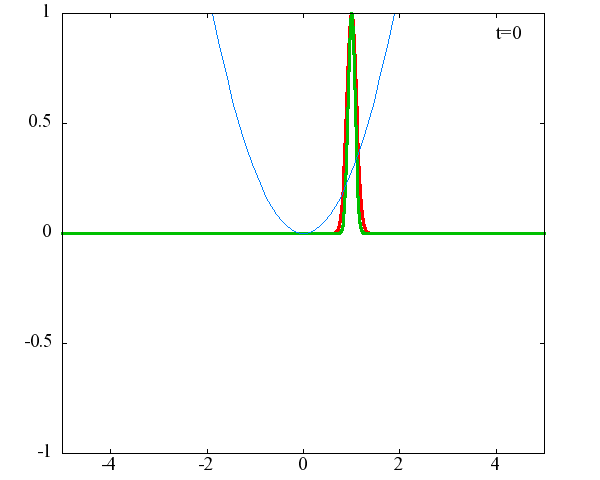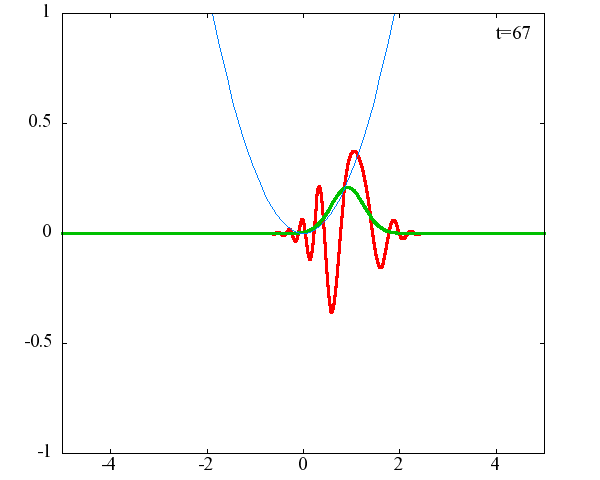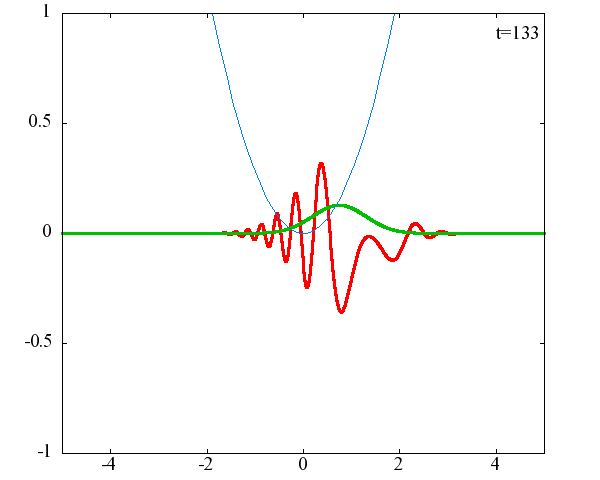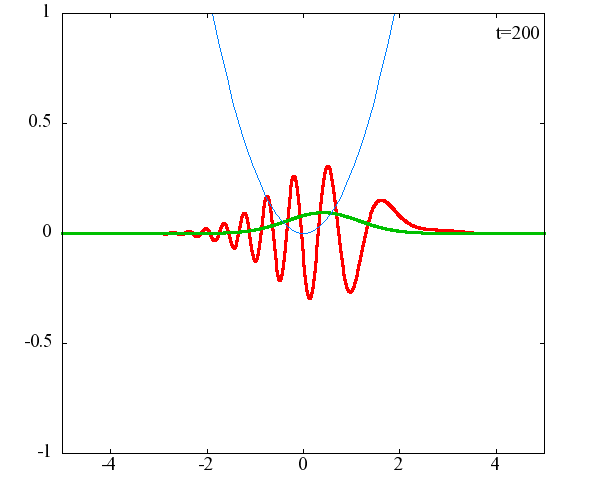
任意の初期状態に対する時間発展の計算結果

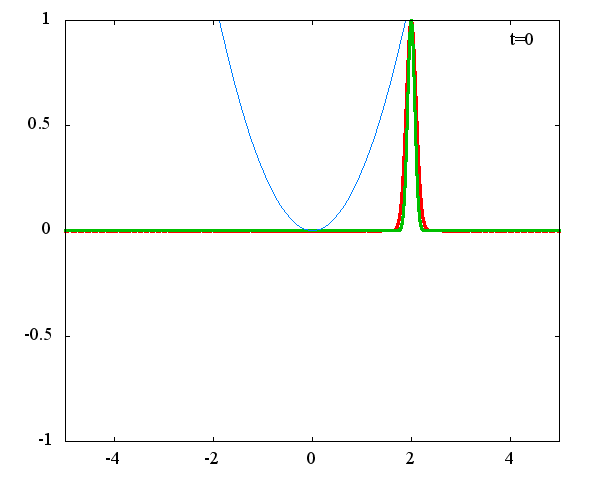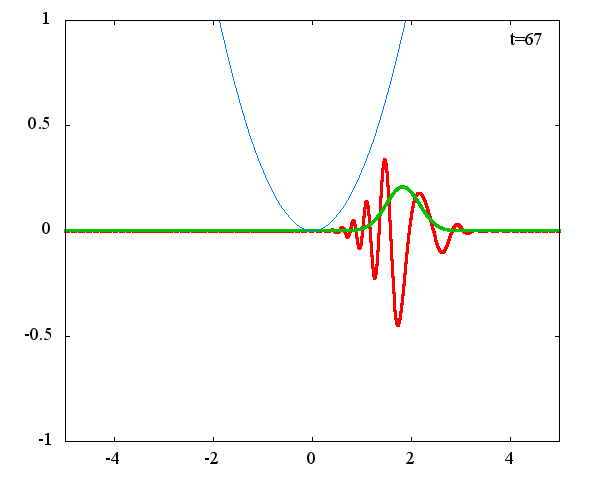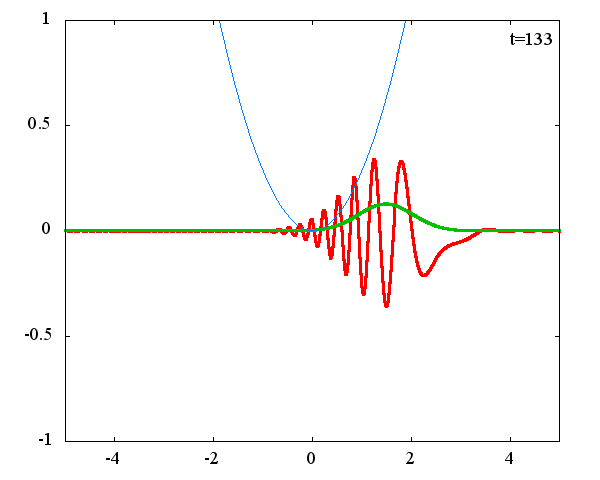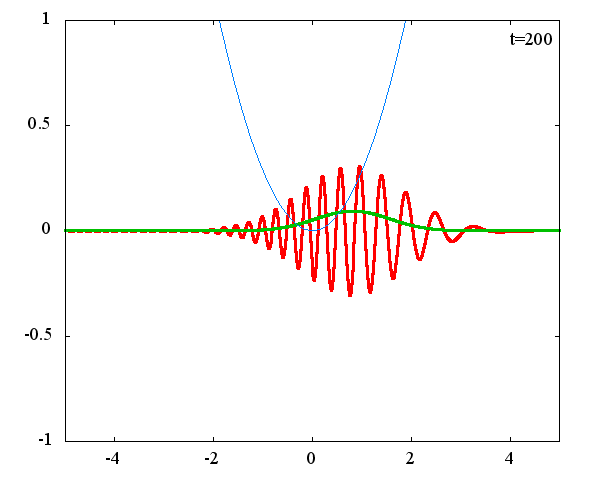
調和振動子の波動関数_任意の初期状態に対する時間発展にて計算しています。 時間発展の時間間隔は 10^{-16}[s]、x 座標の単位は 1[nm] ( = 10^{-9}[m]) です。 なお、グラフの赤線は波動関数の実部、緑線は波動関数の絶対値の二乗です。

初期状態がガウス分布の時間発展

初期状態のガウス分布の中心座標 x_0 = 1.0×10^{-9}[m] or 2.0×10^{-9}[m] 、 幅を決める σ = 1.0×10^{10} or 2.0×10^{10} の場合の計４種類の初期状態に対して時間発展を計算します。

x_0 = 1.0×10^{-9}[m]、σ = 1.0×10^{10}

x_0 = 2.0×10^{-9}[m]、σ = 1.0×10^{10}

x_0 = 1.0×10^{-9}[m]、σ = 2.0×10^{10}

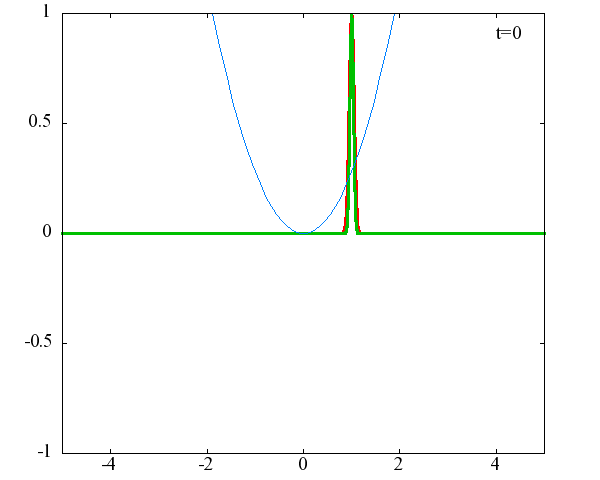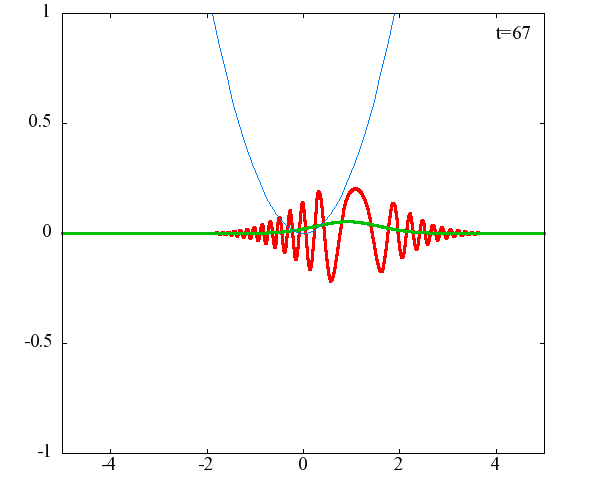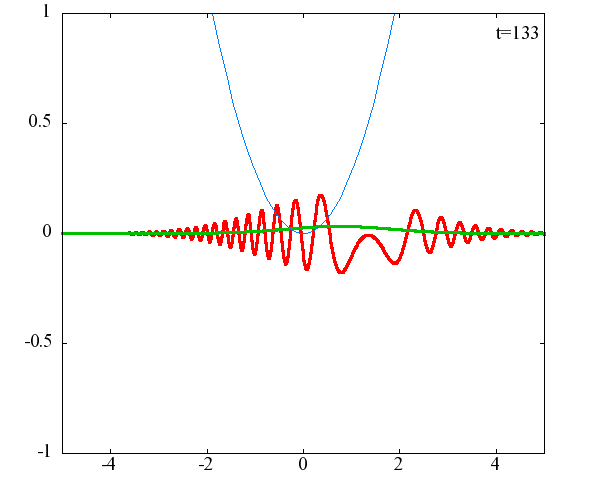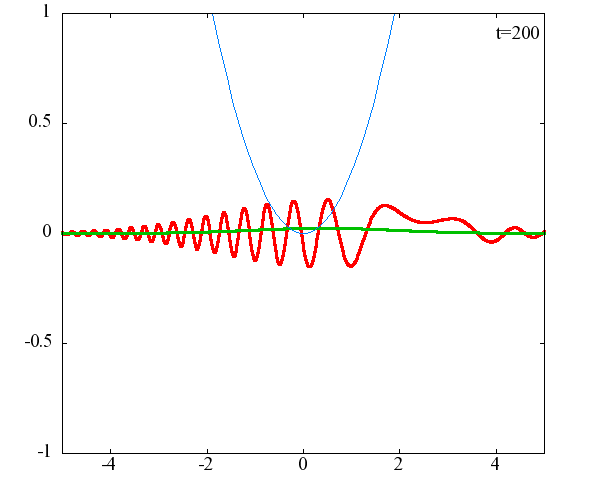
x_0 = 2.0×10^{-9}[m]、σ = 2.0×10^{10}

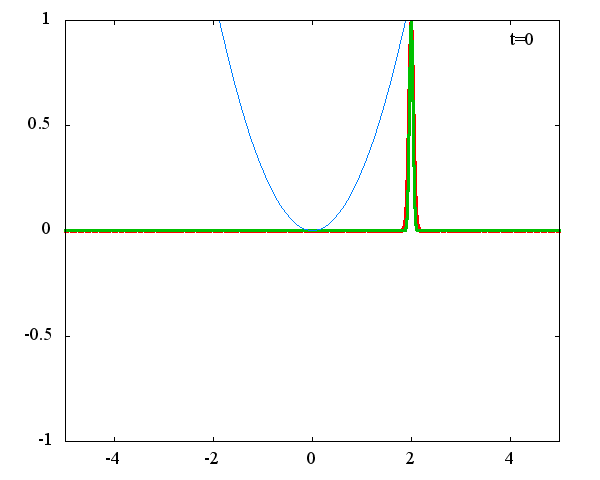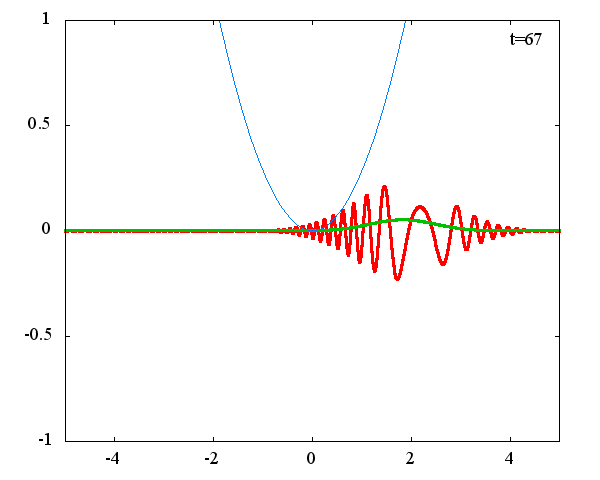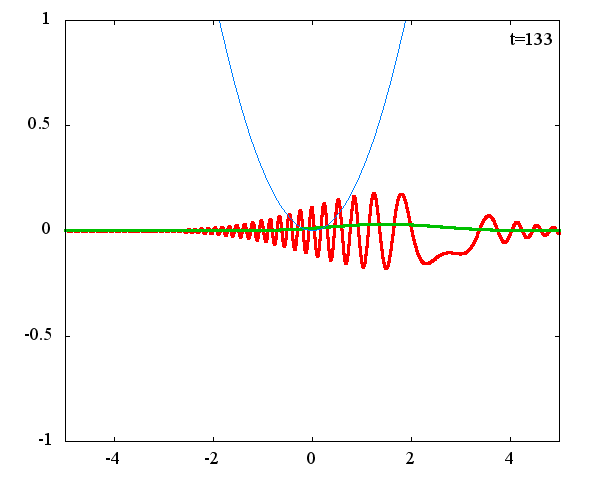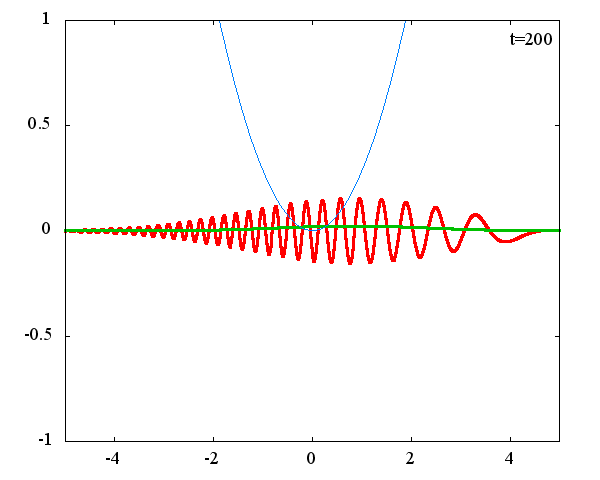
古典力学における調和振動子同様、波動関数の時間発展は周期的になっていることがわかります。 波動関数の絶対値だけを見れば周期はおよそ T = 63 × 10^{-16}[s]、波動関数自体の周期は T = 126 × 10^{-16}[s]であることが確認できます。この t = 63 × 10^{-16}[s] は、ハミルトニアンのポテンシャル項で定義される ω(=1.0×10^{15}[rad/s]) から得られる 周期 T = 2π/ω = 62.8 × 10^{-16}[rad/s] と古典力学における調和振動子の周期と一致することがわかります。 しかしながら、波動関数の周期は T = 126 × 10^{-16}[s]と古典系と比べて２倍となっているようです。 「１次元量子力学における調和振動子における単一エネルギーの時間発展」で示したとおり、各エネルギーで異なる周期 2π/ω(n+1/2)で与えられるにも関わらず、周期が ２× 2π/ω となるのは不思議です。 このことがガウス分布の場合だけなのかどうかを調べるために、ステップ関数でも周期を見ることにします。

ステップ関数時間発展

座標表示における波動関数の初期状態が、式(5)で定義されるステップ関数の場合の時間発展を計算します。 ガウス分布の場合と同様、調和振動子の波動関数_任意の初期状態に対する時間発展にて計算しています。 なお、時間発展の時間間隔は 10^{-16}[s]、x 座標の単位は 1[nm] ( = 10^{-9}[m]) 、グラフの赤線は波動関数の実部、緑線は波動関数の絶対値の二乗です。

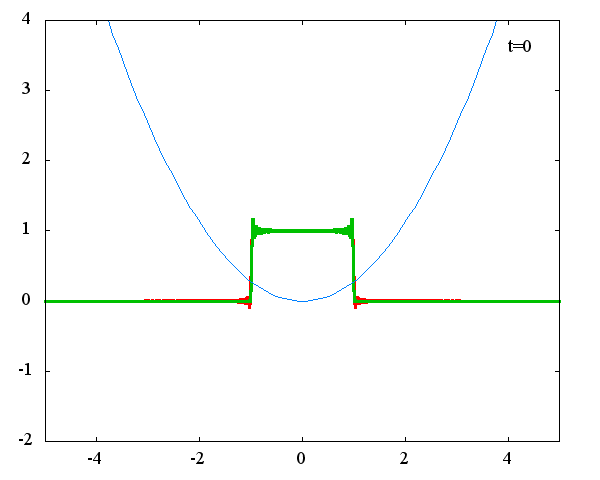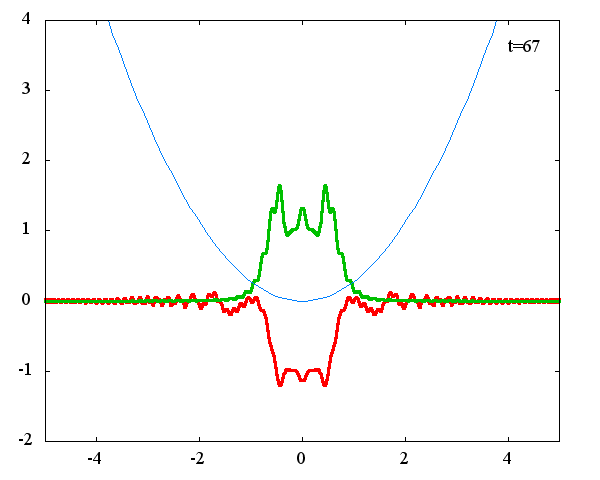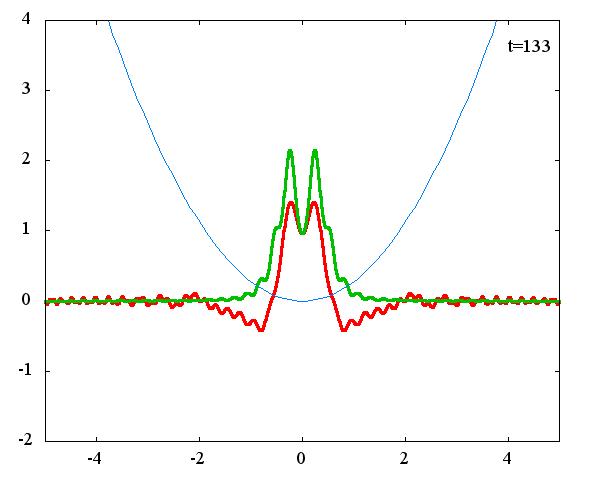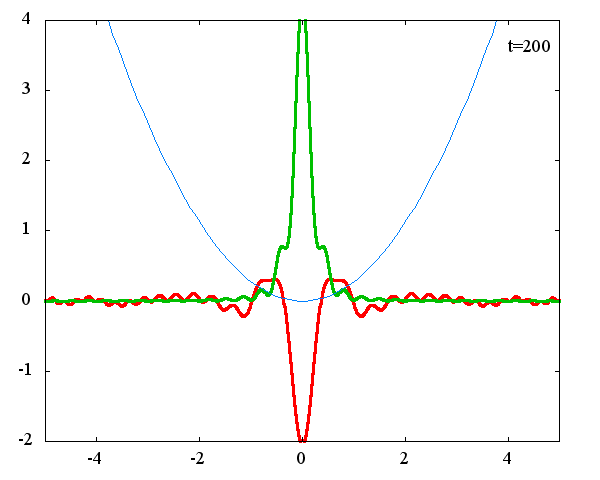
波動関数の絶対値だけを見れば周期はおよそ T = 31 × 10^{-16}[s]、波動関数自体の周期は T = 126 × 10^{-16}[s]であることが確認できます。 「任意の関数をエルミート多項式で展開する」で示したとおり、ガウス分布とステップ関数の展開係数は全く異なりますが、波動関数自体の周期が一致するのは不思議です。

数値計算の考察

１．量子粒子による１次元調和振動子も古典系と同様、周期的な振る舞いをする。
２．量子粒子による１次元調和振動子の周期は、波動関数の絶対値だけで見れば古典系と同じである一方、波動関数の実部（もしくは虚部）だけを見れば、古典系の２倍となる。
３．さらにその周期は波動関数の初期状態（空間分布とエネルギー分布）に依らない。

上記１は自明です。
上記２、３もよく考えれば自明です。 なぜならば、式(2)において n に関して和をとるため、どのような和のとり方でも必ず exp(-iω/2t) の因子が残ることになります。 つまり、初期状態がガウシアンだろうがステップ関数であろうが、最終的な波動関数に exp(-iω/2t) の因子のため、ωに対する２倍周期の振動が現れることになる為です。