１次元量子力学における調和振動子
コヒーレント状態の時間発展

前節「１次元量子力学における調和振動子におけるコヒーレント状態の空間分布」にて、 消滅演算子の固有状態であるコヒーレント状態の座標表記を導出し、空間依存性を調べました。 本節では、本稿の最終目的であるコヒーレント状態の時間発展を計算します。

コヒーレントの時間発展を調べるため、シュレディンガー表式における状態ベクトルのコヒーレント状態表記を考えます。 t=0 で状態ベクトルとコヒーレント状態が一致していると考え、シュレディンガー方程式を用いて時間発展させます。 状態ベクトルのコヒーレント状態表記の一般表式は、

(1)

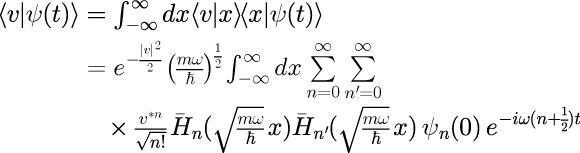
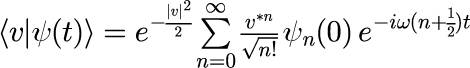
となります。 ただし、各種記号の定義、各固有ベクトルの内積やエルミート多項式の直交性などは、本稿の記事「１、２、３」で示されています。 「１次元量子力学における調和振動子における任意の初期状態に対する時間発展」で示したとおり、式(1)の ψ_n(0) がシュレディンガー方程式に対する積分定数で、各 n に対して任意の値を取ることが許されます。 その自由度を用いて、シュレディンガー表式における状態ベクトルが t = 0 でコヒーレント状態と一致すると考えます。 つまり式で表すと

(2)

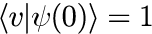
となり、式(1)より

(3)

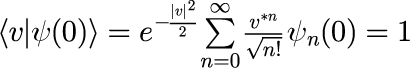
となります。式(3)がψ_n(0)を決めるための条件となり、得られたψ_n(0)を式(1)に代入することで、 t=0 でコヒーレント状態と一致している状態の時間発展を計算することができます。 任意の v に対して式(3)の無限等比級数が 1 に収束するψ_n(0)の関数型は

(4)

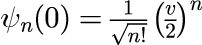
となります。式(4)を式(1)に代入し、和を計算することでコヒーレント状態の時間発展の解析解が得られます。

(5)

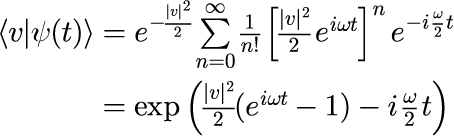
コヒーレント状態の時間発展は角振動数 ω/2 、振幅自体が |v| に依存し、各振動数 ω で振動する波であることがわかります。 式(5)を変数 |v| と t の関数でプロットしたのが次の図です。

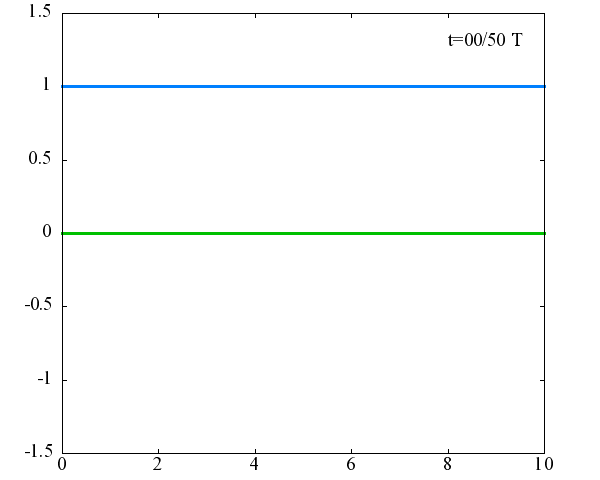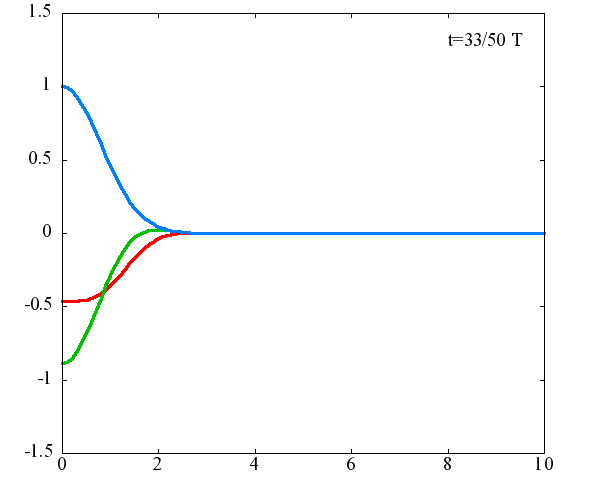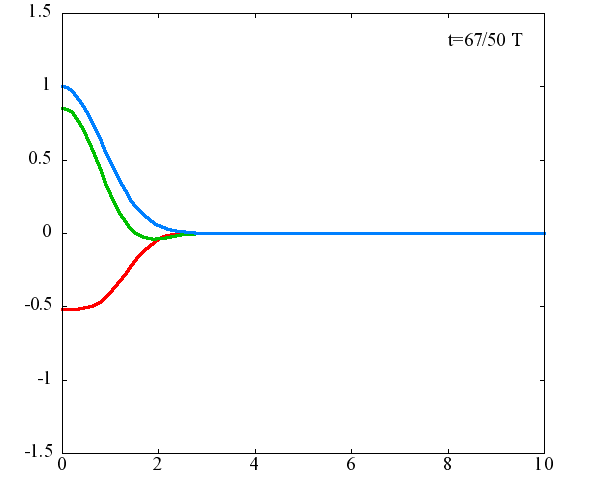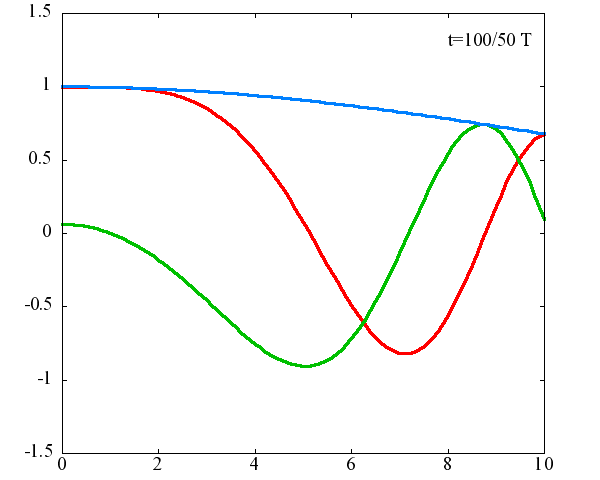
図の横軸が |v|、縦軸が <v|ψ(t)> であり、赤線は<v|ψ(t)>の実部、緑線は虚部、 青線は絶対値です。図中の T はωで決まる周期 T ≡ 2π/ω を表します。

本稿のまとめ

１次元量子力学の調和振動子における様々な状態の時間発展について数値計算しました。 著者の不勉強もありますが、次のことがわかりました。

１．１次元調和振動子において、実空間における任意形状の時間発展は、周期 2T [s] (T=2π/ω)の運動をする。ただし、波動関数の絶対値だけを見れば周期は T[s] である。
２．コヒーレント状態の座標表記による空間依存性はガウシアンを包絡関数とする平面波であり、中心座標と平面波の波数が v に依存する。 ただし、ガウシアンの半値全幅は v に依存しない。
３．シュレディンガー表記による状態のコヒーレント表記を用いた時間依存性は、振幅が|v|とωに依存し、角振動数ω/2で振動する。