シンプソン法を用いた複素数を含んだ２重積分(C++)

シンプソン法とは積分を数値積分するための手法です。
本稿では複素数を含んだ２重積分をシンプソン法を用いて計算します。

【参考】シンプソン法については「シンプソン法を利用して積分を数値計算する」、シンプソン法を用いた２重積分については「２重積分の計算をシンプソン法を用いて計算する（C++）
」をご覧ください。

被積分関数を f(x,y) として、

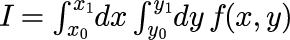
を計算します。本稿では f(x,y)も積分値 I も複素数となる点に注意が必要です。 プログラムの動作確認のための例として、被積分関数

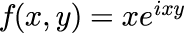
に対して、xとyの積分範囲をそれぞれ[0:1]、[-π:π]として計算します。 積分値の解析解は 4/πです。 数値解と解析解を比較して、誤差を確認します。

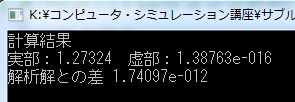
およそ、分割個数 N =1000 で誤差は 10^{-12} 程度となり、 誤差は h^{4}程度であることを確かめることができます。 分割個数と誤差の関係は「シンプソン法を利用して積分を数値計算する」をご覧ください。

C++プログラム

/*
複素数を含んだ２重積分(シンプソン法)
例：F(x,y) = x * exp(I* x* y) x[-PI:PI] y[0:1]
*/
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include <cstdio>
#include <iomanip>
#include <stdio.h>
#include <complex>
#if defined(_OPENMP)
  #include <omp.h>
#endif
#if defined(_MSC_VER)
  #include <direct.h>   // Windowsフォルダ作成用
#elif defined(__GNUC__)
  #include <sys/stat.h> //  UNIX系ディレクトリ作成用
#endif
using namespace std;

double PI = acos(-1.0);
const complex<double> I = complex<double>(0.0,1.0);

complex<double> Simpson2(complex<double> **f, const int m, const int n, double h1, double h2);
complex<double> F(double x, double y) //被積分関数
{
  return x*exp(I*x*y);
}


int main(void){
  double h1, h2, x,y,exa ;
  int i, j;

  const int m = 1000; //x軸の刻み数
  const int n = 1000; //y軸の刻み数
  double x0 = 0.0 , x1 = 1.0 ; //xの積分範囲
  double y0 = -PI , y1 = PI ; //yの積分範囲
  complex<double> **f= new complex<double>*[m+1];  // double型 m+1 個分の領域を動的確保
  for (i= 0; i<=m; ++i) f[i]= new complex<double>[n+1];  // double型 n+1 個分の領域を動的確保

  for(i = 0; i <= m; i++){
    for (j = 0; j <= n; j++)  {
      x = x0 + (x1-x0)/double(m) * double(i);
      y = y0 + (y1-y0)/double(n) * double(j);
      f[i][j] = F(x,y);
    }
  }
  h1 = (x1-x0) / double(m);
  h2 = (y1-y0) / double(n);
  exa = 4.0/PI; // 解析値
  complex<double> s = Simpson2(f, m, n, h1, h2); // 計算

  for (i= 0; i<=m; ++i) delete[] f[i]; // 動的に確保した領域をそれぞれ解放
  delete[] f;

  //結果の書き出し
  cout << "計算結果"<< endl;
  cout << "実部："<< s.real() <<  "  虚部：" << s.imag() << endl; 
  cout << "解析解との差 "<< abs(s.real() - exa)/exa << endl; 
  cin.get();
  return 0;
}

complex<double> Simpson2(complex<double> **f, const int m, const int n, double h1, double h2)
{
  int i, j;
  complex<double> v;
  complex<double> *temp;
  temp = new complex<double>[m+1];  //double型 m+1 個分の領域を動的確保

  for(i = 0; i <= m; i++){
    v = - f[i][0] + f[i][n];
    for(j = 0 ; j < n - 1; j += 2)
      v += (2.0 * f[i][j] + 4.0 * f[i][j + 1]);
    temp[i] = v;
  }
  v = - temp[0] + temp[m];
  for(i = 0; i < m - 1; i += 2)  v += (2.0 * temp[i] + 4.0 * temp[i + 1]);
  delete [] temp;
  return v * h1 * h2 / 9.0;
}