１次元量子力学における調和振動子
n励起状態の運動量表示

「１次元量子力学の調和振動子における任意の初期状態に対する時間発展」では、実空間における任意の分布に対する時間発展を計算しました。このシリーズの続きとして、初期運動量分布を与えた場合の時間発展を計算します。 その準備として本節では、 n番目のエネルギー準位、つまり n励起状態の に対する状態の運動量表記を与え、どのような分布になるのかを調べます。

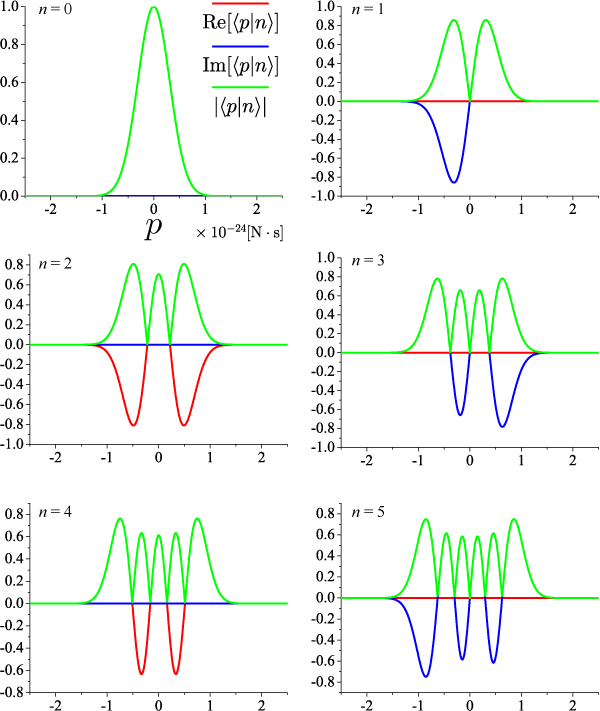
n励起状態は個数演算子 N の固有状態で与えられます。 n励起状態の座標表記（<x|n>）による実空間分布はエルミート多項式を用いて表すことができますが、 n励起状態の運動量表記（<p|n>）がどのようになるのでしょうか。数値計算結果をプロットしてみます。 n励起状態の運動量表記は

(1)

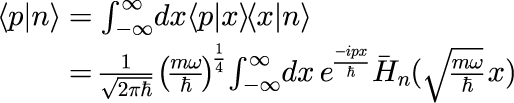
を計算することで得られます。 途中の式変形では、

(2)

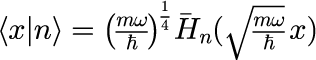
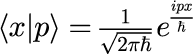
を用いました。 各nに対する運動量分布は次の図のとおりです。

１次元調和振動子のn励起状態の運動量表示

図の横軸が p、縦軸が <p|n> であり、赤線は<p|n>の実部、青線は虚部、 緑線は絶対値です。

計算結果の考察

計算結果から運動量分布も規格化エルミート多項式と非常に似ていることがわかります。 ただし、座標表記では実数ですが運動量表記の場合には虚数部も持つ点が異なります。 似ている理由は、式(1)にて規格化エルミート多項式を具体的に書いて部分積分を繰り返すことで、似ている複素数を含んだ多項式が導出できます。 次節では、このn励起状態の運動量分布を用いて、初期状態における任意の運動量分布を作り出すことを考えます。