異なる媒質の境界における電磁波と電子波
【2-3】電子波に対する透過係数と反射係数の導出

前節では、 異なる媒質の境界における電磁波に対する透過係数と反射係数の導出を行いました。 そこから、ブリュースター角や臨界角といった特別な角度が存在することをみました。 本節では、シュレディンガー方程式から出発して、電磁波と同様、境界条件から透過係数と反射係数の導出を行います。

シュレディンガー方程式の反射係数と透過係数

異なる媒質が接している場合の境界条件の導出を行います。 一様媒質中での電子波の平面波は「【1-2】平面波の時間発展」で示したとおり、

(2-3-1)

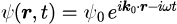
で与えられます。は波動関数、は波数ベクトルで、 「【1-1】一般解の表式と平面波」で示したとおり、波数ベクトルの方向と電子波の進行方向と一致します。また、 媒質の情報は、波数ベクトルと角振動数との関係を表す分散関係

(2-3-2)

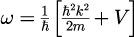
の中に現れる屈折率を通じて平面波に取り入れられます。 一様な媒質中を伝搬してきた電子波が異なる媒質の境界面に差し掛かると、透過波と反射波とに分けられます。 このことを調べるために、下図のように図の左右を軸、上下を軸とし、画面に垂直方向が軸とします。

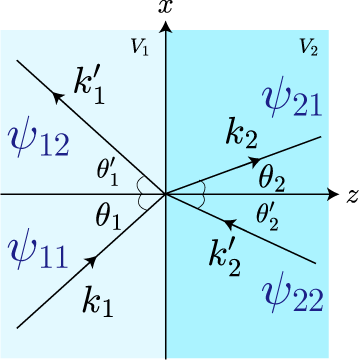
が媒質の境界を表し、がポテンシャルの媒質１で、がポテンシャルの媒質２とします。 黒矢印を波数ベクトル、すなわち電子波の進行方向を表します。 媒質１内での波動関数を

(2-3-3)

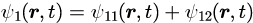
と表し、同様に媒質２でも、

(2-3-4)

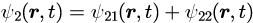
とします。図中の、、、は、各媒質における左右進行波の振幅を表します。

(2-3-5)

(2-3-6)

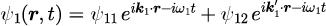
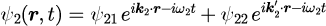
ただし、波数ベクトルは式(2-1-3)で示したとおり

(2-3-7)

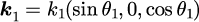
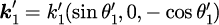
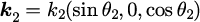
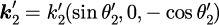
です。式(5),(6)において、未知の変数は上記の4つに加えて、と２つです。つまり、６つの変数の関係を表す６本の方程式があれば完全に解けることになります。 ６つの変数の関係式はシュレディンガー方程式から導かれる境界条件

境界面上における波動関数の連続性

(2-3-8)

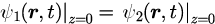
境界面上における波動関数の微係数の連続性

(2-3-9)

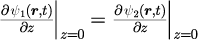
から導出することができます。

波動関数の連続性から

任意の時刻で式(8)が成り立つためには、電磁波の場合と同様、各媒質中の角振動数が

(2-3-10)

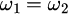
となる必要があります。角振動数が媒質によらず一定値をとるということを意味します。 この式と式(2)で表された分散関係と合わせることで、各媒質における波数ベクトルの大きさの関係を導くことができます。

(2-3-11)

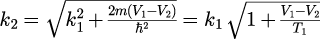
ただし、は媒質中における電子波のエネルギー

(2-3-12)

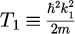
です。式(11)からわかるとおり、領域２の波数ベクトルの大きさは電子波のエネルギー（波数ベクトルの大きさ）に依存します。 これは屈折率にしか依存しない電磁波の場合とは異なります。

話を元に戻して、式(10)を考慮すると式(8)は、

(2-3-13)

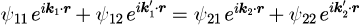
となります。さらに境界面におけるすべてので式(13)が成り立つためには、

(2-3-14)

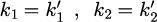
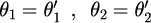
と

(2-3-15)

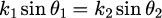
が成り立つ必要があります。式(15)は電磁波の境界面におけるスネルの法則と同じ表式になります。 もう少し強調して言えば、境界面と水平成分の連続性から、式(12)は波動現象の一般的現象であることがわかります。 式(13)に式(14)と(15)を代入すれば、最終的には

(2-3-14)

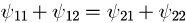
が得られます。

波動関数の微係数の連続性から

式(9)のz微分の結果、波数ベクトルの成分が指数部分から降りてきます。 式(11)と(12)を考慮すると、

(2-3-14)

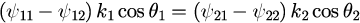
が得られます。 以上より、各媒質における波動関数の振幅の関係式

(2-3-14)

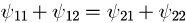
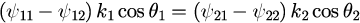
が得られました。式(14)は未知の変数４つに対して方程式が２本なので足りないように思えますが、 初期状態を適切に与えることによって、式(14)から透過係数と反射係数を得ることができます。

透過係数と反射係数

式(14)は境界面における波動関数の振幅の関係を表しているので、 初期状態を適切に与えることで境界面がひとつしかない場合の透過係数と反射係数を計算することができます。

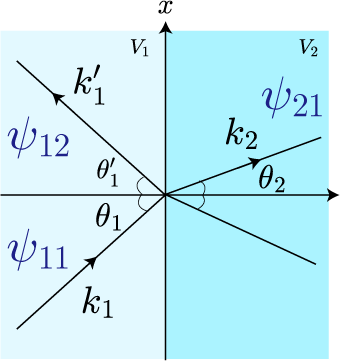
上図を見ても分かる通り、であるので、 を入射波として考えた場合、 に対するが反射係数、 に対するが透過係数と呼ばれます。 反射係数と透過係数の具体的な表式は

(2-3-15)

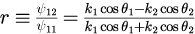
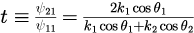
となります。ただし、とは式(15)と(13)でそれぞれ決定することができます。 電磁波と同様に、入射角に対する反射係数と透過係数の振る舞いを調べます。

透過係数と反射係数の関係

式(15)から透過係数と反射係数の関係式を導出することができます。

(2-3-16)

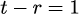
この表式は電磁波におけるS偏光の場合と一致します。

反射係数と透過係数の計算結果

内部反射と外部反射

境界面における反射や透過を議論する際、 ポテンシャルの大きな媒質から小さな媒質への場合と、逆にポテンシャルの小さな媒質から大きな媒質への場合で、 反射波・透過波の振る舞いが大きく異なります。

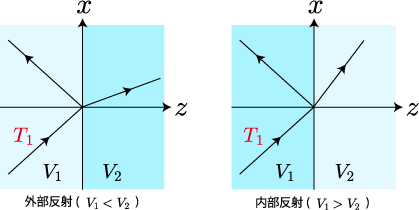
上図は上記の２つの状況の模式図です。 絶縁体中の電磁波と同様、を外部反射、を内部反射と呼ぶことにします。 境界面における透過波と反射波の振る舞いにおいて、電子波の振る舞いは電磁波の場合と異なり、領域２の波数ベクトルの大きさが、領域１の運動エネルギーに依存します。つまり、境界面における電子波の振る舞いを考える場合、２つの媒質のポテンシャルを与えるだけでなく、 入射波の運動エネルギーを与える必要があります。本節では、入射波の運動エネルギーに対して、外部反射、内部反射における反射係数と透過係数の角度依存性を計算結果を示します。 その際に、反射係数と透過係数を

(2-3-17)

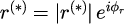
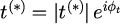
と、大きさと位相に分けてプロットします。ただし、は外部反射を意味すると内部反射を意味するのどちらかを表します。

外部反射、内部反射の大きさの角度依存性

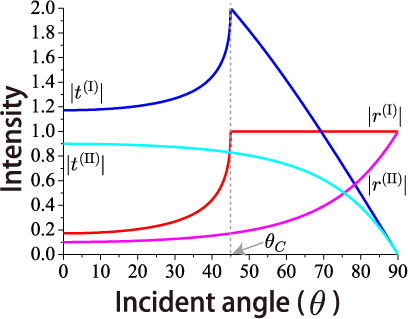
図中のは臨界角で、外部反射にて臨界角以上の入射角で全反射がおきます。 臨界角は、式(15)のスネルの法則においてを満たす入射角で与えられます。 臨界角をとすると

(2-3-18)

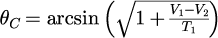
となります。本節で計算した外部反射は入射波の運動エネルギー、であるので、式(18)からと臨界角が得られます。 また、図から透過係数の大きさは入射角が臨界角のときに最大値をとることがわかります。 式(15)にを代入すると、

(2-3-19)

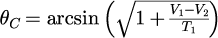
となり、パラメータに依存しないことがわかります。

外部反射、内部反射の大きさの偏角の角度依存性

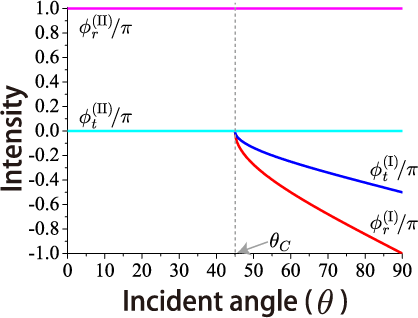
内部反射の場合、入射角に依らず反射係数と透過係数は実数になります。 ただし、反射波の位相は逆になります。 一方、外部反射の場合、入射角が臨界角以下では透過係数と反射係数は実数となり、臨界角以上では複素数となる

/*
シュレディンガー方程式による境界面による反射係数と透過係数
(公開：2011/12/08)
*/
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include <cstdio>
#include <iomanip>
#include <stdio.h>
#include <complex>
#if defined(_OPENMP)
  #include <omp.h>
#endif
#if defined(_MSC_VER)
  #include <direct.h>   // Windowsフォルダ作成用
#elif defined(__GNUC__)
  #include <sys/stat.h> //  UNIX系ディレクトリ作成用
#endif
using namespace std;

const double PI = acos(-1.0);
const double e = 2.7182818284590452354;
const complex<double> I = complex<double>(0.0,1.0);
const double c = 2.99792458E+8;
const double lambda0 = 500.0E-9;
const double mu0 = 4.0*PI*1.0E-7;
const double epsilon0 = 1.0/(4.0*PI*c*c)*1.0E+7;
const double h  = 6.6260896 * 1.0E-34;
double hbar = h/(2.0*PI);
const double me = 9.10938215 * 1.0E-31;
const double eV = 1.60217733 * 1.0E-19;

double T1 = 2.0*eV; //初期運動エネルギー
double V1 = 1.0*eV, V2 = 0.0*eV;

double k1  = sqrt(2.0*me*T1/pow(hbar,2)); 
const double theta_s = 0.0, theta_e  = 90.0; 
const double theta_k = 0.1;
string folder = "Schrodinger";//作成するフォルダ名

char str[200];
int main(){
  #if defined(_MSC_VER)
    _mkdir(folder.c_str());   // Windowsフォルダ作成
  #elif defined(__GNUC__)
    mkdir(folder.c_str(), S_IRWXU | S_IRWXG | S_IRWXO); // UNIX系のディレクトリ作成
  #endif
  #if defined(_OPENMP)
    omp_set_num_threads(8);
    cout << "OpenMPを利用します（最大スレッド数："<< omp_get_max_threads() << "）" <<  endl;
  #endif


  string S_p = folder + "/coefficient_1-0.data";
  ofstream ofs_p( S_p.c_str() );
  
  ////////////////////
  //角度ごとに計算
  ////////////////////
  for(double th=theta_s; th <=theta_e; th+=theta_k )
  {
    double Theta= PI/180.0 * th;     //弧度法へ変換
    double cos1 = cos(Theta);
    double sin1 = sin(Theta);
    complex<double> k2 = sqrt( complex<double>( pow(k1,2)+(2.0*me*(V1-V2))/pow(hbar,2) , 0.0));
    complex<double> sin2 = k1/k2 * sin1;
    complex<double> cos2 = sqrt( 1.0 - pow(sin2,2));
    complex<double> r = (k1*cos1-k2*cos2)/(k1*cos1+k2*cos2);
    complex<double> t = (2.0*k1*cos1)    /(k1*cos1+k2*cos2);
    ofs_p  << th  << " " << abs(r) << " " << arg(r)/PI  <<  " " << abs(t) << " " <<arg(t)/PI  <<endl;
  }
}

ファイル

■シュレディンガー方程式による境界面による反射係数と透過係数

【目次】シュレディンガー方程式とマクスウェル方程式

• ０．導入
  　【0-1】はじめに
  　【0-2】本稿で取り扱う基礎方程式
• １．一様媒質中における一般解と具体例
  　【1-1】一般解の表式
  　【1-2】平面波の時間発展
  　【1-3】１軸ガウシアンによる光パルスと電子パルス　（１軸ガウシアンによる電子パルスの拡散）
  　【1-4】２軸ガウシアンによる光パルスと電子パルス　（２軸ガウシアンによる電子パルスの拡散, ２軸ガウシアンによる光パルスの拡散）
  　【1-5】３軸ガウシアンによる光パルスと電子パルス
  　【1-6】垂直１軸ガウシアンによる光ビームと電子ビーム
  　【1-7】垂直２軸ガウシアンによる光ビームと電子ビーム
  　【1-8】直線偏光と円偏光
  
• ２．異なる媒質の境界における電磁波と電子波
  　【2-1】異なる媒質の境界における波動の一般論
  　【2-2】電磁波に対する透過係数と反射係数の導出
  　【2-3】電子波に対する透過係数と反射係数の導出
  　【2-4】境界面において任意の形状の波に対して時間発展を与える一般表式
  　【2-5】境界面における平面波電磁波の時間発展
  　【2-6】境界面における平面波電子波の時間発展
  　【2-7】境界面における１軸ガウシアンによる光パルスと電子パルスの時間発展
  　【2-8】境界面における２軸ガウシアンによる光パルスと電子パルスの時間発展
  　【2-9】境界面における３軸ガウシアンによる光パルスと電子パルスの時間発展
  　【2-10】境界面における垂直１軸ガウシアンによる光ビームと電子ビームの時間発展
  　【2-11】境界面における垂直２軸ガウシアンによる光ビームと電子ビームの時間発展
  
• ３．転送行列法
  　・電子のトンネル確率
  　・光のトンネル効果
  
• ４．１層バリアにおける光パルスと電子パルスのシミュレーション
• ５・ポテンシャル障壁による量子粒子のトンネル時間
• ６・フォトニックバンドギャップによる光パルスのトンネル時間
• ７．無限周期構造中の分散関係，群速度，位相速度
  　・転送行列とブロッホの定理
  　・ブロッホ波数と透過係数の関係
  　・分散関係
  　・透過係数と群速度の関係
  
• ８．有限サイズの結晶における光パルスと電子パルスの横断時間
  　・光パルスと電子パルスの横断時間の導出
  　・パルス伝搬速度と群速度の関係
  
• ９．フォトニックバンド端における光パルスの遅延
  　・１次元フォトニック結晶における透過係数と横断時間の数値計算
  　・横断時間の解析解
  
• １０．バンド端における電子パルスの遅延
  　・１次元クローニッヒ・ペニーモデルにおける透過係数と横断時間の数値計算
  　・横断時間の解析解
  
• １１．非周期構造における光パルスと電子パルスと伝搬