プランクの放射法則
３．完全導体で囲まれた空洞における各電場モード振幅の温度依存性

量子力学の創成に重要な影響を与えたプランクの放射法則のシミュレーションを行います。
本稿では、完全導体で囲まれた真空中における電磁波の基本モードを用いた各種シミュレーションを次のステップで行います。
１．プランクの法則の解析解
２．完全導体で囲まれた空洞における電磁波の基本モード
３．完全導体で囲まれた空洞における各電磁波モード振幅の温度依存性
４．任意の温度に対する完全導体中の電磁波シミュレーション

完全導体中には特定の電磁モードのみの存在が許されることは「２．完全導体で囲まれた空洞における電磁波の基本モード」で示したとおりです。 しかしながら、各電場モードの強度は任意ではなくエネルギー量子仮説に従う必要があります。 つまり、各電場モードの強度は

(1)

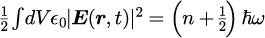
を満たす必要があります。 左辺は空洞内の電磁波のエネルギー、右辺は角振動数に対する量子化されたエネルギーを表します。 はの電磁波の励起数を表します。 電磁波の励起数の平均値はカノニカル分布から

(2)

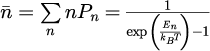
と与えられます。は温度に依存し、 が大きくなるほども単調増加します。

以上のことを調べるために、本節では下図のような有限サイズの完全導体中の電磁波について考えます。

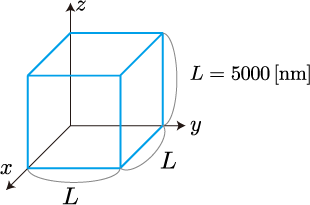
電磁波の具体的表式は「完全導体で囲まれた空洞における電磁波の基本モード」の式(3)で与えられ、式(1)の積分を実行することをができます。

(3)

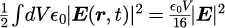
つまり、各電場モードの振幅は式(1)(3)から

(4)

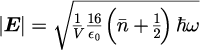
と決まります。つまり、任意の温度に対する各電場モードの振幅が得られることになります。 各電場モードの振幅を計算する手順は次のとおりです。

（１）完全導体のサイズと温度を指定する
（２）を指定する　→　が得られる
（３）が得られる　→　角振動数の電場の振幅が得られる

各電場モードの振幅の計算結果

黒体放射のサイズ、温度における 各電場モードの振幅を計算した結果が次のグラフです。

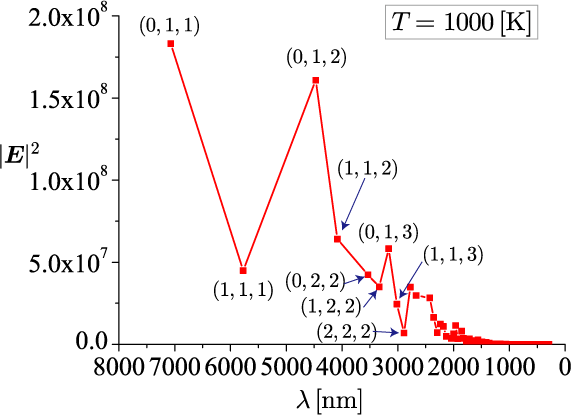
横軸は電磁波の波長、縦軸は電場の振幅です。 各点は完全導体内で存在可能なモードを表します。ただし、図中のの振幅は、との振幅の合計となります。 は最低次の電場モードで、ではが最も波長の長い電磁波となります。 に比較しての電場モードの振幅が小さいのは、同じ波長となるモードが１パターンしか存在しないためです。つまり、同じ波長となるモード数が多いほど電場の振幅が大きくなります。

次のグラフはに対する結果を示します。

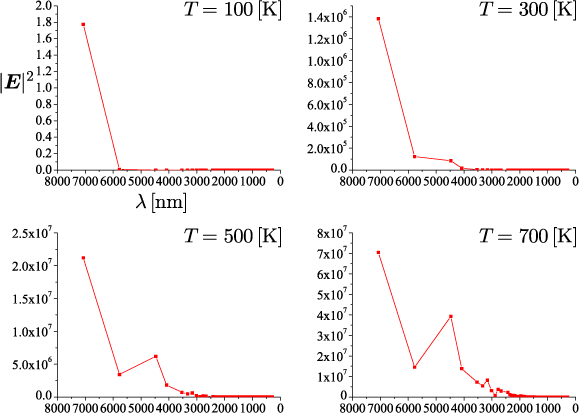
ではほとんど最低次のモードしか存在してないことがわかります。 各温度で縦軸は同じスケールなので、とを比較すると、の電場強度は非常に小さな値であることがわかります。