プランクの放射法則
4.任意の温度に対する完全導体中の電磁波シミュレーション
量子力学の創成に重要な影響を与えたプランクの放射法則のシミュレーションを行います。
本稿では、完全導体で囲まれた真空中における電磁波の基本モードを用いた各種シミュレーションを次のステップで行います。
1.プランクの法則の解析解
2.完全導体で囲まれた空洞における電磁波の基本モード
3.完全導体で囲まれた空洞における各電磁波モード振幅の温度依存性
4.任意の温度に対する完全導体中の電磁波シミュレーション
本稿の目的である「プランクの放射法則」の理解の最後として、任意の温度に対する完全導体中の電場の時間発展を計算します。
完全導体中の電磁波復習ついでに、計算までの道筋を示します。
(1)完全導体中の電磁波のモード
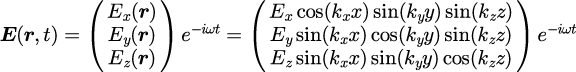
は互いに独立ではなく、
電磁波の波数ベクトル
によって決まります。ただし、電磁波の振幅は任意です。
と
の関係は、
「2.完全導体で囲まれた空洞における電磁波の基本モード」
で示したとおりです。
(2)エネルギーの量子化による電場強度の制限
「3.完全導体で囲まれた空洞における各電磁波モード振幅の温度依存性」で示したとおり、 エネルギーの量子仮説を課すことで、電場強度は
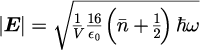
となります。
ここで重要なのは、平均励起数は温度
と角振動数
に依存することです。つまり、エネルギーの量子仮説は電磁波の振幅に制限を加えることを意味します。
ただし、
は電磁波の波数ベクトル
で決まります。
(3)電場強度の決定と各電場モードの重ね合わせ
完全導体中の任意の電場は、
電磁波の波数ベクトル
と垂直で、互いにも垂直な
、
に分解することができます。
さらに、熱によって励起された電磁波の各電場振幅
は(等重率の原理的に?)等しいと仮定します。つまり、
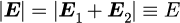
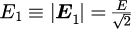
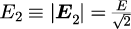
と表せます。くどいですが、,
は、波数ベクトル
に依存します。式(1)に対して、
「2.完全導体で囲まれた空洞における電磁波の基本モード」
で示した
の関係を踏まえて、
各モード
の電磁波は
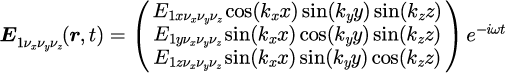
となります。も同様です。
任意の温度
に対する最終的な電場は、
各モード
に対する電場の和で得られます。また、
も加えます。つまり、
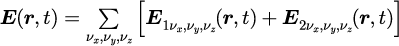
となります。
任意の温度に対する完全導体中の電磁波シミュレーション
一辺がL=5000[nm]の完全導体中の電磁波Ezの時間発展(温度 T=300[K])。
横軸 x[nm]
縦軸 y[nm]
カラーバー:電場強度 [a.u.]
時間間隔:Δt=10^{-16}[s]
※z=L/2 の断面における電場を描画
では、
「2.完全導体で囲まれた空洞における各電磁波モード振幅の温度依存性」で示したとおり、ほとんど最低次のモードしか励起していないため、時間的に周期的な振る舞いとなっています。
では、
「2.完全導体で囲まれた空洞における各電磁波モード振幅の温度依存性」で示したとおり、最低次のモードとあと2つのモードしか励起していません。ただし、
と比べて、電場の振幅は約800倍です。
では、
「2.完全導体で囲まれた空洞における各電磁波モード振幅の温度依存性」で示したとおり、様々なモードが励起されています。それにともなって、
電場の振幅は約10000倍です。

































