ベクトルと関数のおはなし
はじめに
ベクトルとか関数といった言葉を聞いて,何を思い出すだろうか? ベクトルは方向と大きさを持つ矢印みたいなもので,関数は値を操作して別の値にするものだ, と真っ先に思うだろう. 実はこのふたつの間にはとても深い関係がある. この「深い関係」を知れば,さらに数学と仲良くなれるかもしれない. そして,君たちの中にははすでに,その関係をそれとは知らずにただ覚えている人もいると思う. このおはなしは,君たちの中にある断片化した数学の知識をつなげるための助けになるよう書いてみた. もし,これを読んで「数学ってこんなに奥が深くて,面白いんだな」と思ってくれれば,それはとってもうれしいな.
ベクトルと関数は一緒だ
ベクトルと関数は一緒だ!と突然言われても,たぶん理解できないだろう. 「一緒だ」というのは,同じ演算ができるよ!という意味での「一緒」なのだ. たとえば
- 1. 和について閉じている:ベクトルの和はベクトルだし,関数の和は関数だよ
- 2. 和の結合法則が成り立つ:ベクトルも関数も,足し算をする順番は関係ない
- 3. 和の交換法則が成り立つ:ベクトルも関数も,足し算を逆にしてもいい
- 4. 零元の存在:ベクトルには零ベクトルがあるし,関数には0がある
- 5. 逆元の存在:ベクトルも関数も,あたまにマイナスつければ,足し算の逆(引き算)ができる
- 6. スカラー乗法の存在:ベクトルも関数も,スカラー倍できる
- 7. スカラー乗法の単位元:ベクトルも関数も,1を掛ければ,同じ物
- 8. 和とスカラー倍についての分配法則:ベクトルも関数も,スカラーを掛けてから足しても,足してからスカラーを掛けてもいい
「こんなの当たり前じゃん!」と言ってしまえばそれまでなのだが,数学的に大切なことなので書いておこう. 「この法則が成り立たないものなんてあるのか?」と思った人はWikipediaで「ベクトル空間」とか「群論」とかを調べてみればいいと思うよ.
さてここで,「関数に内積なんてあるのか!?」と思った人がいるかもしれない. そうだ!内積が定義できないと「ベクトルと関数は一緒だ!」なんて言えない. けど,実はあるんだな,関数にも内積が. ちょっと長い話になるけど,お付き合いいただけたらと思う.
ベクトルの内積
さて,まずは「ベクトルとは何か」「内積とはどういう時に使えるのか」ということについて考えてみよう. 君たちは,二次元のベクトルを数式で書くときに,無意識に以下の書き方をしているだろう.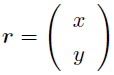
ここで,を任意とすると,二次元平面内にあるすべての点を表すことができるが,
これが何を表しているか考えたことはあるかい?
実は,(1)というのは基底を定義することによって,はじめて成り立つのだ.
この場合だと,
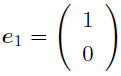
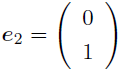
という基底を「選んでいる」. この基底を使って(1)を書き直すと
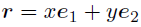
この「係数付きの和をとる」という表し方を線形結合という.
実は基底はに限らず,どんなベクトルを選んでもいいのだ.
いや,言い過ぎた....「非零かつ互いに線形独立な」ベクトルならば,基底にできるのだ.
二次元平面の場合では,長さがあって平行じゃないってことだ.
たとえば,いま二次元平面内のある点
が
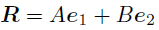
で,表されるとする.
ここで,非零かつ平行でないベクトルの線形結合として,
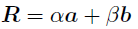
と,表すこともできる.
じゃあ,係数と
はどうやって求めるの?
ここで内積の出番なのだ!
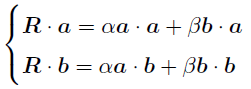
連立方程式(7)を解けばが求められるのだが,なんだかメンドクサイ...
そう思った君には朗報で,実は(5)の両辺と
の内積をそれぞれとれば
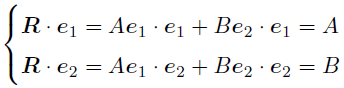
と,連立方程式を解かずに一発で係数を求められるのだ! この「便利な基底」のお話は次の節でしようと思う. とりあえず,いまここで分かって欲しいのは内積をとれば係数を求められる!ということだ. ちなみに,(8)は以下のように書き換えることもできる. 「なんでわざわざこんなことをするのか」と思うかもしれないが, 読み進めているうちに分かるときがくるので,頭の片隅にでも置いておいてくれ.
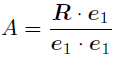
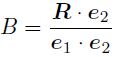
関数の内積
さて,ここでは「関数の内積とは何か」ということについて考えてみよう. まず,唐突だが以下の微分方程式
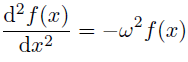
を満たす解について考えてみる.
この解はまあいろいろな表し方があって
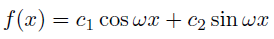
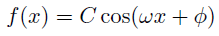
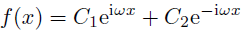
となるけど,今回は(14)について考えようと思う.
この式と(4)が似ていると思った君は鋭いね!
実は微分方程式(11)の解はすべて,
という関数系(関数の集合)を基底として表すことが出来るのだ!
(特異解とかあるかもしれんけど,今は気にしないでくれ....)
いま,「すべての」解は(14)で表せると言った.
つまり,これは二階微分方程式なので,(14)の二つの定数
を任意とすると全ての解をカバーできるのだ.
この「すべての解」の集合を微分方程式(11)の解空間という.
「関数が空間を作る」なんて直感的には分かりにくいかもしれない.
でも,基底
があるんだからなんかベクトルっぽいし,
ベクトルの係数を任意にすると空間を表現できるように
を任意としてすべての解を表すこともできる.
「ベクトルと関数は一緒だ」と思えてきたんじゃないか!?
さて内積のお話に戻ろう.
いま解空間中のある一つの解を
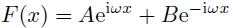
と表すとする.
この係数を求めるにはどうすればいいのか?
「え?話が逆じゃね?
を定めると
が定まるんだろ?いまさら求める必要ないじゃん」
と思った君には「係数
を,
を使って表すにはどうするか?」
というふうに問いを言い換えておこう.
ここで,
は
に依存しない係数である,ということを強調して言っておく.
まずは
を求めてみよう.
にかかっている関数
を消す(1にする)ため,
(14)の両辺に
の複素共役
をかける.
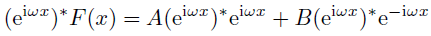
ここでになるからって,
としてしまうと,
が
に依存してしまい定数ではなくなってしまう.
そこで,(16)の両辺を
について区間
で積分する.
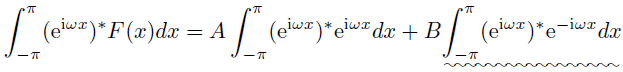
(17)の下線を引いた部分が0になることは分かるだろうか.
被積分関数がになり,オイラーの公式より
という周期関数の和になることをうまく利用すれば求められるはずだ.
あとは両辺を
で割るだけだ.
やっと
を求めることができた.
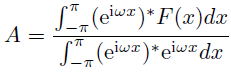
計算すれば分母はになるのだが,
メンドクサイ何か法則性を見出せそうなので,そのままにしておく.
同様にも求められる.
分母を
にしないのは,決してメンドクサイからとかそういう不純な理由ではない!本当だ.
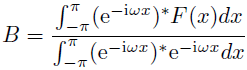
さてここで,前の項ではベクトルは「内積をとれば」「係数を求められる」と言った.
関数の場合は,「ある関数の複素共役をかけて積分するという操作をすれば」「係数を求められた」.
ということは,ある関数の複素共役をかけて積分するという操作を関数の内積と定義できないだろうか!
もう少し一般的でカッコイイ書き方をしてみよう.
区間上で定義される関数
について,
内積
を以下のように定義する.
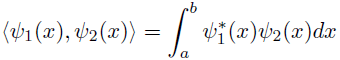
この定義にしたがって(18),(19)を書き換えてみると
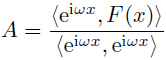
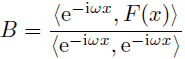
と,見事に(9)(10)と対応がとれているではないか! どうやら,この関数の内積の定義はうまくいきそうだぞ!!
ベクトルと関数の「大きさ」
せっかく内積のお話をしたので,ここでベクトルと関数の「大きさ」の話についても触れておこう.
をベクトルのノルムという.
この場合,ベクトルの長さに当たる値である.
もまた,関数のノルムという.
ベクトルと一緒ね.
なんで長さとか大きさじゃなく「ノルム」なんていう難しい言葉を使うかっていうと,
ベクトルにも関数にも使える概念にしたいからなんだ.
さらに抽象的な話をすると,実は最初に挙げた8つのルールはベクトル空間という, 線形代数学などで重宝される集合の定義になっているのだ. さらに,この「ノルム」という概念を追加するとヒルベルト空間というものになる. ベクトルも関数も,ヒルベルト空間というものを形成しているんだ! (ベクトルだからって,ベクトル空間を形成するわけではないことに注意だ!)
便利な基底の選び方・作り方
ここでは「便利な基底とは何か」について考えてみようと思う. 先ほど出てきたベクトルの係数を求める式
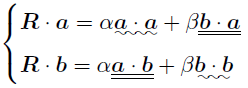
と
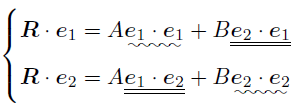
を見比べてみよう. どうやら,
- [条件1.] 二重下線部が零になるかどうか.
- [条件2.] 波下線部が1になるかどうか.
が計算が楽になるポイントらしい!
しかも,条件1.のほうが条件2.よりも重要に思える.
前節「関数の内積」のときも,となってくれたおかげで,連立方程式を解くことなく楽に計算を進めることができたし.
このポイントを踏まえて,これからのお話を聞いてほしい.
一般的な話をするから,がんばって聞いてくれ!
次元空間内の任意の点
は,非零かつ互いに線形独立なベクトルの集合
を基底とし,これらの線形結合で表すことができる.
つまり
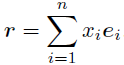
ただしは任意である.
このとき,次の条件をみたす基底を直交基底と呼ぶ.
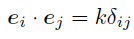
ただし,は定数である.
さらに,この定数
としたとき,つまり下記の条件をみたす基底を正規直交基底と呼ぶ.
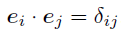
直交基底は先ほど挙げた条件1.をみたし,正規直交基底は条件1.と2.どちらもみたすことは分かってくれたかな?
あと,"線形独立 直交
正規直交"という対応関係も分かったかな?
前節を読んでくれた君なら分かると思うが,関数でも同じことが言えるね. ただ,関数の場合は基底が無限個あることがある,ということに気をつけてほしい. たとえばフーリエ級数展開などがいい例だね.
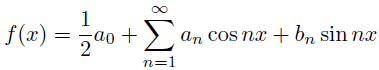
これは無限個の要素を持つ関数系を基底として
を表しているのだ.
このフーリエ級数展開ついては,あとで詳しく説明するぞ.
「基底が無限個ある」という点だけを留意してくれれば,あとはベクトルと一緒だ.
関数
が非零かつ互いに線形独立な関数系
を基底として表されるとき.
つまり
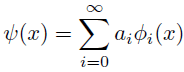
ただしは任意である.
このとき,次の関係をみたせば
は直交基底であり,特に
のときは正規直交基底である.
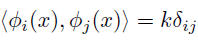
さて,「便利な基底の選び方」は分かったね.
次は「便利じゃない基底から便利な基底を作る方法」について考えてみよう.
正規直交基底ではないベクトル基底から,正規直交基底
を作り出す方法をGram-Schmidtの正規直交化法という.
次の操作を機械的にやれば,正規直交基底を作れる.
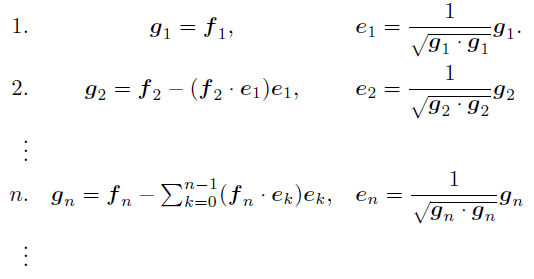
さて,上の操作がどんな意味を持っているか,分かったかな?
たとえば,2番目の真ん中の操作を見てみよう.
から,
の中にある
と平行になる成分
を消している.
こんなことをするだけで,
直交するベクトル
を作ることができるのだ!
ためしに,2.の真ん中の式の両辺に
をかけると,
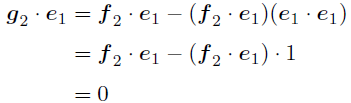
となり,直交することが分かる.
あとはノルムで割って正規化してるだけだね!
番目も同様で,
番目までの基底について,平行となる成分をそれぞれ消していることが分かる.
関数についても,全く同じ方法でできて,正規直交基底ではない関数基底から,正規直交基底
を次のやり方で作れる.
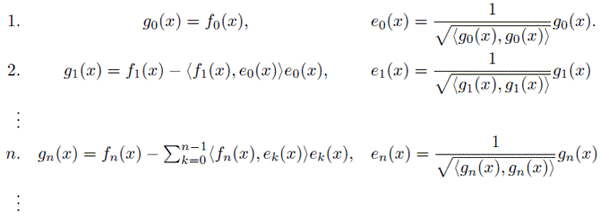
関数をベクトルで表す
君たちは,二次元ベクトルを表すとき,
無意識にこんな書き方をしているよね.
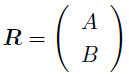
これは,正規直交基底というのを「選んできて」線形結合した,
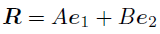
の係数を書いているのだ! ということは,今までのお話を聞いて分かったかな? ここで,「関数にも基底があって,それらの線形結合で表すことができる」ということから, 関数も(29)のような表記ができるんじゃないか!と思った君,賢いね! ということで,ここではその表記について考えていこう.
区間で定義される関数
が,正規直交基底
の線形結合で表されるとする.
(といきなり言ってみたが,ここまで読んできた君たちにはこの言葉が通じるって信じてる!)
もし互いに線形独立だけど直交じゃない基底があったら,前の説で紹介したGram-Schmidtの正規直交化法を使って,なんとかしてくれ!
...よし話を戻そう.
つまりこういうことだ.
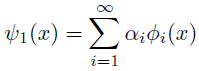
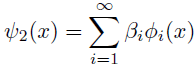
ただし,
は任意である.
このときの
と
の内積
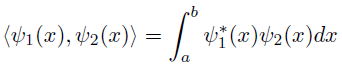
について考えてみよう.
(33)の右辺に(31),(32)を代入し,下記の演算を施す.
は正規直交基底なので
になる.
よって都合よくクロスターム
(
のときの
,下式の下線を引いた部分)が0になるのだ.
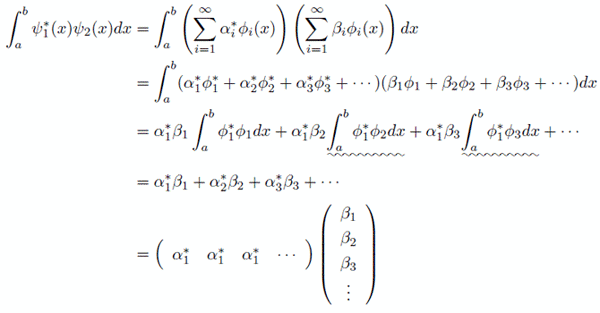
ここで,ケットベクトル なるものを下記のように定義する.
このケットベクトルというのは,関数を指定するための無限次元ベクトルになっている.
だって,基底にかかる係数を要素とする行列だからね!
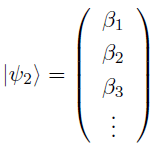
次にブラベクトル なるものも定義する.
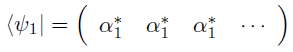
このブラベクトルは,見て分かるとおりケットベクトルを転置して共役をとったものになる.
この操作は「ダガー」""を使って表される.
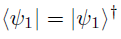
このブラベクトルとケットベクトルを使えば,関数の内積を表せる. つまり
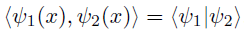
(ブラベクトルとケットベクトルを掛け合わせると,なぜか真ん中の棒""が一本へるのだ.)
このようなブラベクトルとケットベクトルを用いた表記法をブラケット表記という.
量子力学にも出てくる,なかなかに奥が深い表記法なのだ!
複素共役をとるという違いはあるけど,転置行列をかけることによって内積を求めるという操作は,ベクトルと一緒だね!
...さあ,だんだんと関数とベクトルの違いが分からなくなってきただろう?
この世のすべてをあらわす
「はじめにベクトルと関数は一緒だ!ときて, しまいにはこの世のすべてをあらわすときたもんだ! とうとうアタマがおかしくなったんじゃないか!?」 と思った君,あながち間違いじゃない. 「この世のすべてをあらわす」というのは誇張しすぎたな. 正確にはこの世のすべての関数を,三角関数を基底としてあらわすということを伝えたいんだ. つまり.このお話をここまで読んできた君ならば,この世のすべての関数を表せるのだ!
すべての周期がである連続周期関数
を考えてみよう.
つまり,
は以下の等式をみたす.
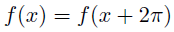
「いきなり話を限定してるじゃないか!もうすべての関数なんて表せないよ!」
と思った君は正解だけど,まあ聞いてくれ.
あとでこの周期を無限大なり何なりの値にすれば,すべての関数を表せるから大丈夫だ!
さて,この周期関数を表すには,どんな基底を選んだらいいだろう?
ここでパッと思いつくのが,関数系(
は整数)である.
幸いこいつらは,
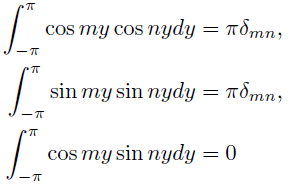
という性質を持っている. いままでにお話しした表記法にすると,こうなる.
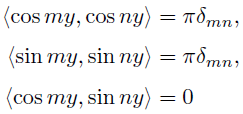
おお,こいつらは直交基底じゃないか!しかも,で割って正規化すると
正規直交基底にもなれるぞ!
ということで,こいつらの線形結合で表してみよう!
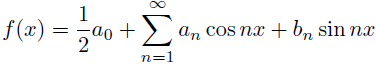
あれ,これフーリエ級数展開じゃね? そう!まさにフーリエ級数展開なのだ! 違う角度から,いつもなんとなく「メンドクセー」と思いながら 使っている式を見ることができたな! ちなみに分かってると思うけど,係数は
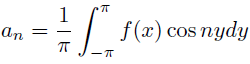
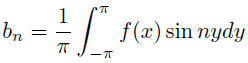
で求められる.
この展開に使われた関数系が,
すべての周期が
である連続周期関数
を表すことができること,
つまり完全性を今から証明する.
証明を行うにあたり,背理法を用いる.
つまり,
『関数系で表せない関数があるとすると,
この関数系に含まれる関数全てと直交する基底
が存在し,
こいつを使ってその関数を表さなくちゃいけない.』
という仮定から,を用いて論理を展開し,矛盾点を導くことで完全性を証明する.
さて,まずは下ごしらえだ.
(39)に(40)と(41)を代入し,下式の操作を行う.
ただ積分と総和の計算順序を入れ替えて,足して,三角関数の加法定理を使っただけだよ!
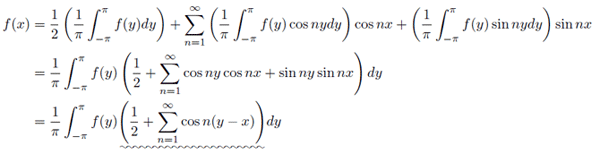
ここで,上式で下線を引いた関数のことをDirichlet核といい,ここではで表す.
つまり
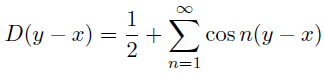
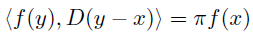
つまり,「ある関数とDirichlet核の内積をとると,
がそのまま戻ってくる」のだ.
この性質を利用して,矛盾を導いてみよう.
関数系
に含まれる関数全てと直交する基底
とDirichlet核との内積をとると,下記の通りとなる.
は関数系
に含まれる関数全てと直交するので,これらの関数と内積をとると0になることに注意しながら演算する.
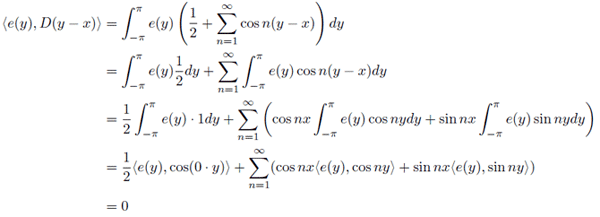
ここで,「ある関数とDirichlet核の内積をとると,
がそのまま戻ってくる」という性質を思い出してみよう.
つまりこういうことだ.
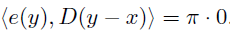
上式から.
ここで,基底となる関数の条件を思い出してみよう.
非零かつ互いに線形独立だったよね.
しかし!非零のはずの
が0になっているという矛盾を導いてしまった.
つまり,先ほど仮定した『関数系
で表せない関数がある』という仮定が間違っていたことになる.
したがって,フーリエ級数展開は完全性を持っているのだ!!!
大げさに言うと,どんなワケのわからない関数でも,どんな複雑な関数でも,
この世のすべての関数は三角関数で表すことができるのだ!!